Матрица и определитель Грама (грамиан) кратко

Привет, Вы узнаете о том , что такое определитель грама, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое определитель грама, грамиан , настоятельно рекомендую прочитать все из категории Линейная алгебра и аналитическая геометрия.

Пусть в евклидовом пространстве 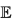известным образом задано скалярное произведение 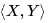. Матрицей Грама системы векторов 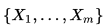называется квадратная матрица, состоящая из всевозможных скалярных произведений этих векторов:

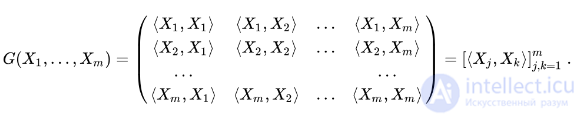
Матрица Грама является симметричной матрицей. Ее определитель называется определителем Грама (или грамиан ом) системы векторов :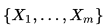

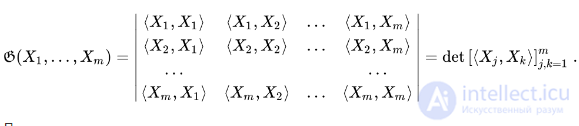
П

Пример. Если в пространстве 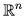строк, состоящих из n вещественных чисел, скалярное произведение определяется по правилу1)

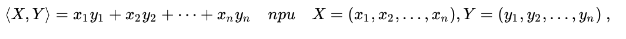
то матрица Грама строк

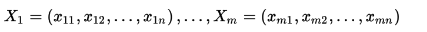
вычисляется перемножением матриц:

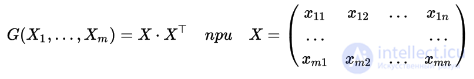
и при T означающем транспонирование. Из теоремы Бине-Коши сразу же следует, что при m>n (числе строк превышающем размерность пространства) определитель грама равен нулю. Этот результат обобщен НИЖЕ для произвольных евклидовых пространств.

Пример. Если в пространстве полиномов с вещественными коэффициентами скалярное произведение задано формулой

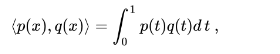
то

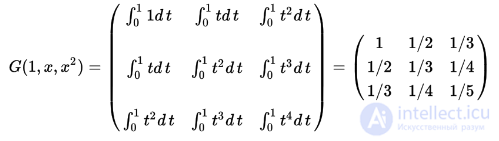
Обобщение получившейся матрицы известно как матрица Гильберта.

Если система векторов образует базис пространства (т.е. пространство является n-мерным), то задание матрицы Грама позволяет свести вычисление скалярного произведения произвольных векторов из к действиям над их координатами:

Линейная независимость векторов

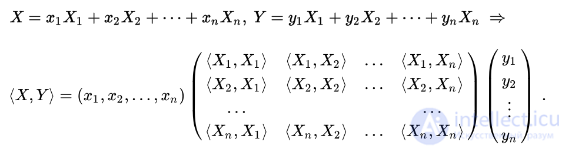
Теорема. 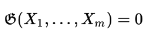тогда и только тогда, когда система векторов 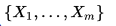линейно зависима.

Доказательство ☞ ЗДЕСЬ.

=>

Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.

Свойства определителя Грама

Теорема. 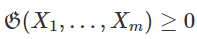для любой системы векторов .

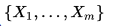Доказательство ☞ ЗДЕСЬ

=>

При m=2 получаем неравенство Коши-Буняковского:

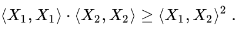
=> Матрица Грама линейно независимой системы векторов является положительно определенной.

Теорема. Пусть 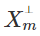означает ортогональную составляющую вектора 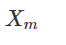относительно 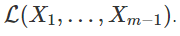. Об этом говорит сайт https://intellect.icu . Тогда

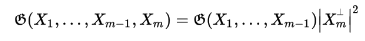
=> Величина определителя Грама не превосходит его главного члена, т.е. произведения элементов его главной диагонали:

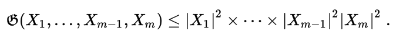
=> Для произвольной квадратной вещественной матрицы

справедливо неравенство Адамара2):

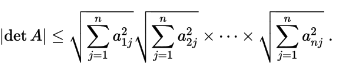
Иными словами: модуль определителя матрицы не превосходит произведения длин его строк. Аналогичное утверждение справедливо и относительно столбцов матрицы.

Доказательство. Обозначим j-ю строку матрицы A через A^|j|. Тогда, поскольку 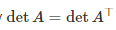, имеем:

при задании скалярного произведения в 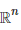стандартным способом. На основании предыдущего следствия, имеем:

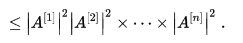
Равенство возможно тогда и только тогда, когда либо все строки попарно ортогональны, либо хотя бы одна строка — нулевая.

Пример.

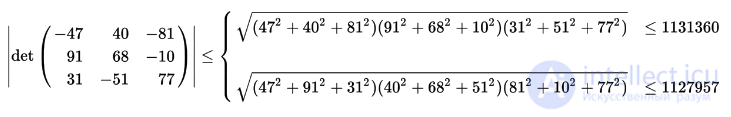
при точной величине определителя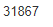

Теорема. Величина определителя Грама не изменится, если к системе векторов применить алгоритм ортогонализации Грама-Шмидта. В обозначениях этого алгоритма имеет место равенство:

Расстояние до линейного многообразия

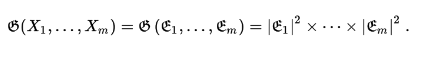
Теорема. Расстояние d от точки Xo 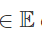до линейного многообразия в

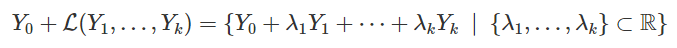
и при фиксированных линейно независимых 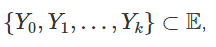, вычисляется по формуле

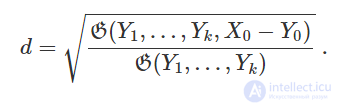
Случай 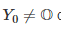сводится к предыдущему сдвигом пространства на вектор (-Yo): см. комментарии к теореме 3

Объемы параллелепипедов

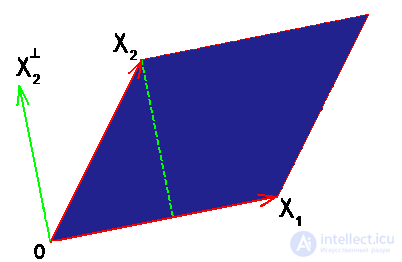
Площадь параллелограмма равна произведению его основания на высоту. Если параллелограмм построен на векторах и из , то за основание можно принять длину вектора , а за высоту — длину перпендикуляра, опущенного из конца вектора на ось вектора .

Аналогично, объем параллелепипеда, построенного на векторах из , равен произведению площади основания на высоту; площадь основания — это площадь параллелограмма, построенного на векторах , а высота — длина перпендикуляра, опущенного из конца вектора на плоскость векторов .

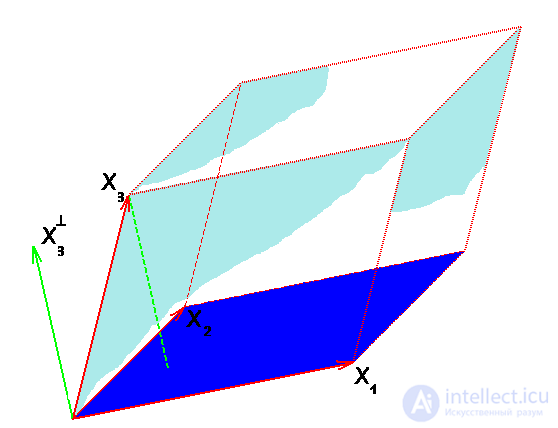
Объем k-мерного параллелепипеда в евклидовом пространстве определим по индукции. Если этот параллелепипед построен на векторах X1, X2, …, Xk−1, Xk , то за его объем примем произведение объема (k-1)-мерного параллелепипеда, построенного на векторах на длину перпендикуляра, опущенного из точки Xk на линейную оболочку векторов (т.е. на длину ортогональной составляющей Xk относительно ):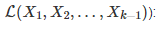

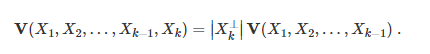
Теорема. Квадрат объема параллелепипеда, построенного на векторах 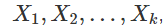, совпадает с величиной определителя Грама от той же системы векторов:

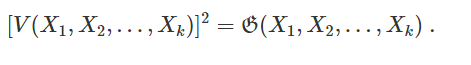
Доказательство следует из представления длины ортогональной составляющей 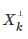через определители Грама (см. теорему 2 и следствие к ней ).

=> Модуль определителя вещественной матрицы

равен объему параллелепипеда в пространстве 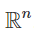, построенного на вершинах с координатами

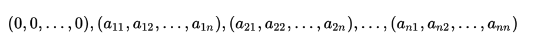
(т.е. «построенного на строках матрицы») и равен объему параллелепипеда построенного на вершинах с координатами

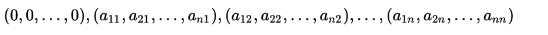
(т.е. «построенного на столбцах матрицы»).

Доказательство фактически совпадает с доказательством неравенства Адамара:

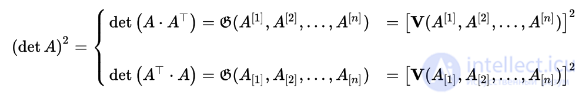
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области определитель грама имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое определитель грама, грамиан и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Линейная алгебра и аналитическая геометрия

Из статьи мы узнали кратко, но содержательно про определитель грама