2.9 Псевдоскалярное произведение кратко

Привет, Вы узнаете о том , что такое псевдоскалярное произведение, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое псевдоскалярное произведение , настоятельно рекомендую прочитать все из категории Линейная алгебра и аналитическая геометрия.

Псевдоскалярным или косым произведением (англ. skew product)векторов и (или ориентированной площадью паралеллограмма, натянутого на вектора и) на ориентированной евклидовой плоскости называется число

где — угол вращения (против часовой стрелки, то есть в положительном направлении) от к . Если хотя бы один из векторов и нулевой, то полагают . В этом определении стоит обратить внимание на то, что понимается под углом . Здесь это не просто обычный угол между векторами, который может принимать значения только от до . Здесь это угол, на который нужно повернуть вектор именно в определенном направлении: против часовой стрелки, и поэтому он может принимать значения от до . Синус такого угла вполне может быть отрицательным, и более того, псевдоскалярное произведение будет менять знак при перемене множителей местами.

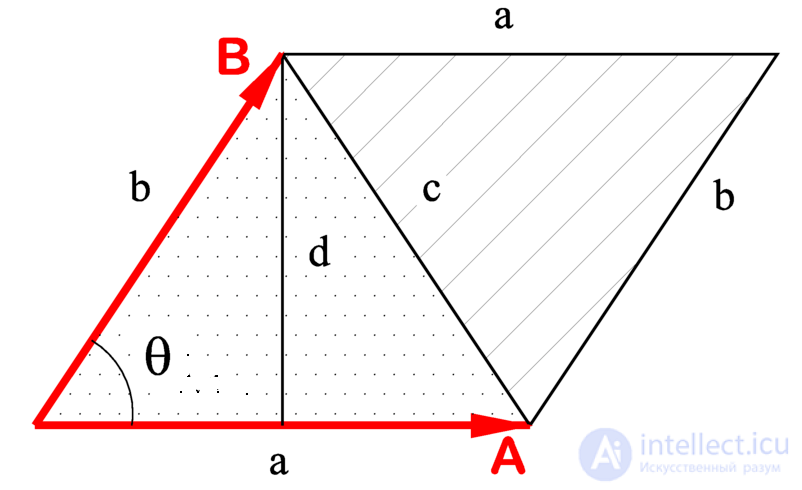
Геометрически псевдоскалярное произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора. С ее помощью удобно работать с площадями многоугольников, выражать условия коллинеарности векторов и находить углы между ними. Псевдоскалярное произведение определяется только для 2-мерных векторов, его аналогом в трехмерном пространстве является тройное скалярное произведение. Также, в некотором смысле аналогом является векторное произведение, из-за чего его иногда тоже неформально называют векторным произведением и обозначают как или.

Определение в линейной алгебре

На ориентированной плоскости

Пусть — ориентированная евклидова плоскость. Число называется псевдоскалярным произведением векторов и , если:

• абсолютное значение равно квадратному корню из определителя матрицы Грама векторов и;
• знак для ненулевого определяется как плюс, если пара векторов и положительно ориентирована, и как минус, если она отрицательно ориентирована.

Не сложно заметить, что это определение равносильно обычному геометрическому определению. Об этом говорит сайт https://intellect.icu . Произведение длин векторов на синус есть площадь паралеллограмма, натянутого на эти вектора. Определитель матрицы Грама же квадрат площади этого же паралеллограма. То, как определяется знак, также понятно: ориентация пары векторов есть направление наименьшего поворота, поэтому если поворот наименьший в положительном направлении, то знак будет положительным, а если в отрицательном, то отрицательный. Аналогично, если поворот наименьший в положительном направлении, то угол будет меньше 180∘, и тогда синус положителен, а если в отрицательном, угол будет больше и синус отрицательный.

На неориентированной плоскости

Пусть — евклидова плоскость. Псевдоскалярное произведение можно определить и для случая, когда положительная ориентация не выбрана, однако тогда результатом произведения будет псевдоскаляр. Псевдоскаляр называется псевдоскалярным произведением векторов и , если:

• абсолютное значение равно квадратному корню из определителя матрицы Грама векторов и ;
• ориентация для ненулевого определяется как ориентация пары векторов и .

Свойства

• Линейность: Здесь , — произвольные вещественные числа.
• Антикоммутативность: .
• Выражение в координатах. Пусть задан базис и два вектора, имеющих в нем координаты . Тогда

Эта формула работает как для псевдоскалярного произведения в ориентированной плоскости, так и для неориентированной. Во втором случае под записями и понимаются числовые значения этих псевдоскаляров в базисе .

Для частного случая ортонормированного положительно ориентированного базиса (если в неориентированной плоскости, то в произвольном ортонормированном базисе) формула имеет вид:

В отрицительно ориентированном базисе эта формула берется со знаком минус.

• Числовое значение псевдоскалярного произведения является инвариантом при всех невырожденных , не включающих отражений.
• Псевдоскалярное произведение — это ориентированная площадь параллелограмма, натянутого на векторы и .
  • Абсолютная величина псевдоскалярного произведения — это площадь такого параллелограмма.
  • Ориентированная площадь треугольника выражается формулой

    

  а его площадь, следовательно, равна модулю этой величины.

• Если рассматривать плоскость в трехмерном пространстве, то

  

где «×» и « ⋅» соответственно — векторное и скалярное произведение, — единичный вектор нормали к плоскости. Знак плюс берется в случае, если правый базис на плоскости, дополненный вектором , образует также правый базис; в противном случае минус.

• — необходимое и достаточное условие коллинеарности ненулевых векторов на плоскости. Нулевой вектор для удобства работы с более употребительным скалярным произведением обычно считают ортогональным любому другому вектору, хотя это является произвольным соглашением.
• Это выражение также можно записать через символ Леви-Чивиты в двумерном пространстве:

Вау!! 😲 Ты еще не читал? Это зря!

• Внешнее произведение
• Смешанное произведение
• Векторное произведение
• Скалярное произведение

Исследование, описанное в статье про псевдоскалярное произведение, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое псевдоскалярное произведение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Линейная алгебра и аналитическая геометрия