Сферическая система координат (азимут и зенит) кратко

Привет, Вы узнаете о том , что такое азимут, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое азимут, зенит , настоятельно рекомендую прочитать все из категории Линейная алгебра и аналитическая геометрия.

Сферическая система координат — трехмерная система координат, в которой каждая точка пространства определяется тремя числами , где — расстояние до начала координат (радиальное расстояние), а и — зенит ный и азимут альный углы соответственно.

Понятия зенит и азимут широко используются в астрономии. Зенит — направление вертикального подъема над произвольно выбранной точкой (точкой наблюдения), принадлежащей фундаментальной плоскости. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. Азимут — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым.

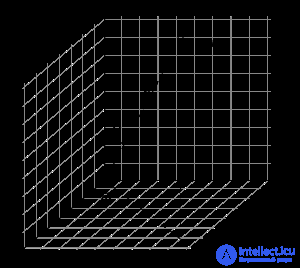
Рис. 1.Точка имеет три декартовых и три сферических координаты

Если рассматривать сферическую систему координат относительно декартовой системы , фундаментальной плоскостью будет плоскость , зенитным углом точки, заданной радиус-вектором , будет угол между и осью , а азимутом — угол между проекцией на плоскость и осью . Это объясняет названия углов и то, что сферическая система координат может служить обобщением множества видов систем небесных координат.

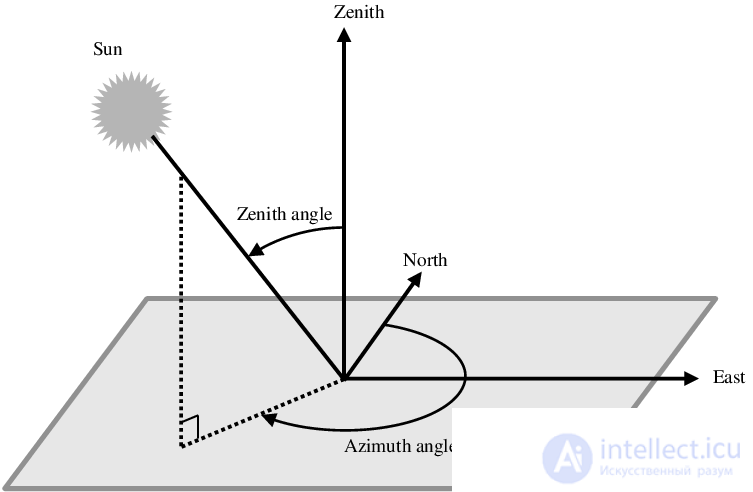
Положение точки в сферической системе координат определяется тройкой , где

• — расстояние от начала координат до заданной точки .
• — угол между осью и отрезком, соединяющим начало координат и точку .
• — угол между осью и проекцией отрезка, соединяющего начало координат с точкой , на плоскость (см. рис. 1).

Угол называется зенитным, или полярным, также он может называться наклонением, или коширотой, а угол — азимутальным. Углы и не определены при , также не определен угол при (то есть при или ).

Такое соглашение установлено в стандарте (ISO 31-11). Об этом говорит сайт https://intellect.icu . Кроме того может использоваться соглашение, когда вместо зенитного угла , используется угол между радиус-вектором точки и плоскостью , равный . Он называется широтой и может быть обозначен той же буквой . Широта может изменяться в пределах . При этом соглашении углы и не имеют значения при , так же как и в первом случае, а не имеет значения при (то есть при или ).

Переход к другим системам координат[

Декартова система координат

Если заданы сферические координаты точки , то переход к декартовым осуществляется по формулам:

Обратно, от декартовых к сферическим:

Якобиан преобразования к сферическим координатам равен

Таким образом, элемент объема при переходе от декартовых к сферическим координатам будет выглядеть следующим образом:

Цилиндрическая система координат

Если заданы сферические координаты точки, то переход к цилиндрическим осуществляется по формулам:

Обратно от цилиндрических к сферическим:

Якобиан преобразования от сферических к цилиндрическим .

Дифференциальные характеристики

Вектор , проведенный из точки в точку , равен

где

ортогональные единичные векторы сферических координат в направлении увеличения , соответственно, а — единичные векторы декартовых координат. Сферические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:

• 
• Квадрат дифференциала длины дуги:

• Коэффициенты Ламе:

• Символы Кристоффеля :

Остальные равны нулю.

Математическое моделирование Земли

Сферическая географическая система координат

Сферическая географическая система координат строится следующим образом :

• ее начало помещено в центр Земли;
• полярная ось направлена по оси вращения Земли;
• координата отсчитывается вдоль радиус-вектора, проведенного из центра Земли;
• полярный угол есть коширота (дополнение географической широты до 90∘ );
• азимутальный угол совпадает с географической долготой (восточной).

Вектор магнитной индукции магнитного поля Земли имеет компоненты

где — магнитное наклонение; — магнитное склонение.

Компоненты вектора ускорения свободного падения равны

Наконец, компоненты вектора угловой скорости вращения Земли такие:

В сферических географических координатах оптимально решать уравнения, описывающие поведение нейтральных частиц околоземного пространства .

Сферическая геомагнитная система координат

Сферическая геомагнитная система координат строится следующим образом :

• ее начало помещено в центр Земли;
• полярная ось направлена по оси магнитного диполя Земли (геомагнитной оси), проходящей через магнитные полюса;
• координата отсчитывается вдоль радиус-вектора, проведенного из центра Земли;
• полярный угол есть геомагнитная коширота (дополнение магнитной широты до );
• азимутальный угол совпадает с геомагнитной долготой, отсчитываемой к востоку от плоскости в западном полушарии, содержащей географический и геомагнитный полюсы.

Географические координаты северного магнитного полюса равны

В сферической геомагнитной системе координат склонение �=0 и

Формулы, связывающие географические и геомагнитные сферические координаты :

В сферических геомагнитных координатах проще, чем в сферических географических координатах, описывать влияние геомагнитного поля на заряженные частицы околоземного пространства .

Вау!! 😲 Ты еще не читал? Это зря!

• Углы Эйлера
• Гиперсферические координаты

Исследование, описанное в статье про азимут, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое азимут, зенит и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Линейная алгебра и аналитическая геометрия

Из статьи мы узнали кратко, но содержательно про азимут