Разложение матрицы,LU-разложение(LR) ,Разложение Холецкого ,Сингулярное разложение

Привет, Вы узнаете о том , что такое разложение матрицы, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое разложение матрицы, lu-разложение , разложение холецкого , сингулярное разложение , настоятельно рекомендую прочитать все из категории Линейная алгебра и аналитическая геометрия.

разложение матрицы — представление матрицы в виде произведения матриц, обладающих некоторыми определенными свойствами (например, ортогональностью, симметричностью, диагональностью). У каждого класса матричных разложений имеется своя область применения; в частности, многие эффективные алгоритмы вычислительной линейной алгебры основаны на построении соответствующих матричных разложений.

Разложения для решения СЛАУ

lu-разложение (LU-декомпозиция, LU-факторизация) — представление матрицы в виде произведения двух матриц, , где — нижняя треугольная матрица, а — верхняя треугольная матрица.

LU-разложение используется для решения систем линейных уравнений, обращения матриц и вычисления определителя. LU-разложение существует только в том случае, когда матрица обратима, а все ведущие (угловые) главные миноры матрицы невырождены .

Этот метод является одной из разновидностей метода Гаусса.

LU-разложение

• Ограничения: матрица — квадратная и невырожденная, причем все ее ведущие главные миноры отличны от нуля .
• Вид разложения: , где — нижняя треугольная матрица, а — верхняя треугольная. Для однозначности разложения обычно дополнительно требуют, что матрица была унитреугольной, т. е. треугольной матрицей с диагональными элементами, равными единице (иногда вместо этого требование унитреугольности накладывают на матрицу ) .
• Сходные разложения: LDU-разложение в виде , где — нижняя унитреугольная матрица, — верхняя унитреугольная, а — диагональная.
• Сходные разложения: LUP-разложение в виде , где — матрица перестановок (выбирается в процессе построения разложения), нижняя унитреугольная матрица, — верхняя треугольная матрица. Это — обобщение LU-разложения на случай произвольных невырожденных матриц.
• Существование: LUP-разложение существует для любой квадратной матрицы . Когда матрица сводится к единичной матрице, LUP-разложение сводится к LU-разложению.
• LUP и LU-разложения используются при решении СЛАУ размерности . Соответствующие методы представляют собой варианты матричной формы метода Гаусса. Матрица характеризует при этом совокупный эффект перестановок строк в методе Гаусса.

Алгоритм LU-разложения

Один из алгоритмов для вычисления LU-разложения приведен ниже

Будем использовать следующие обозначения для элементов матриц: , , , ; причем диагональные элементы матрицы , =1… .

Найти матрицы и можно следующим образом (выполнять шаги следует строго по порядку, так как следующие элементы находятся с использованием предыдущих):

1. Цикл i от 1 до n
   1. Цикл j от 1 до n
      1. u_ij=0, l_ij=0
      2. l_ii=1
2. Цикл i от 1 до n
   1. Цикл j от 1 до n
      1. Если i<=j:
      2. Если i>j:

В итоге мы получим матрицы — и .

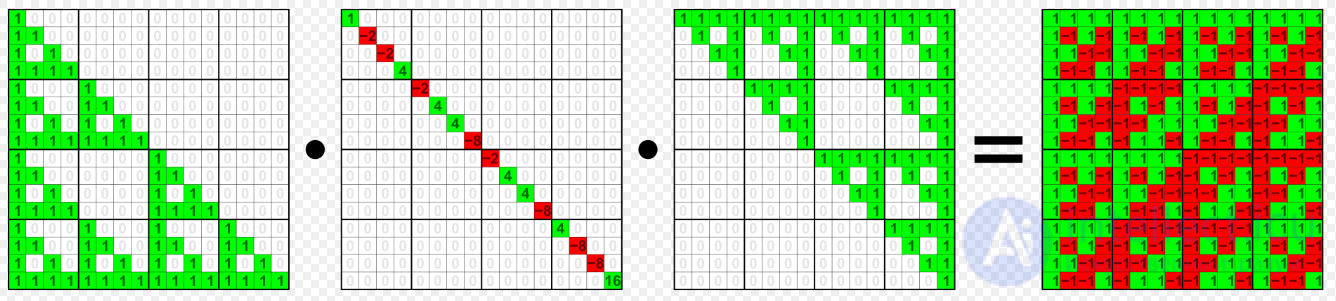рис. LDU-разложение матрицы Уолша

Ранговая факторизация Ранговая факторизация

• Ограничения: произвольная матрица размера и ранга .

• Вид разложения: , где — матрица и — матрица .
• Ранговая факторизация может быть использована для вычисления псевдообратной матрицы, которая применяется при отыскании общего решения СЛАУ .

разложение холецкого

• Ограничения: симметричная положительно определенная матрица .
• Вид разложения: (или, что эквивалентно, ), где матрица — верхняя треугольная (соответственно, матрица — нижняя треугольная) .
• Сходные разложения: альтернативой является модифицированное разложение Холецкого (LDL-разложение), которое позволяет избежать извлечения корней (в нем матрица — нижняя унитреугольная, а — диагональная).
• Разложение Холецкого единственно.
• Разложение Холецкого также применимо, если матрица эрмитова и положительно определена.
• Разложение Холецкого применяется для решения СЛАУ , если матрица имеет соответствующие свойства. Об этом говорит сайт https://intellect.icu . Этот способ решения, по сравнению с методом LU-разложения, заведомо численно устойчив и требует в два раза меньше арифметических операций .

QR-разложение

• Ограничения: произвольная матрица размера .
• Вид разложения: , где — ортогональная матрица размера , и — верхняя треугольная размера .
• Сходные разложения: существуют аналогичные QL-, RQ- и LQ-разложения.
• В силу ортогональности матрицы (что означает совпадение обратной матрицы с транспонированной матрицей ) система � эквивалентна системе с треугольной матрицей, решение которой не доставляет труда.
• Одним из способов получения матрицы является процесс Грама ― Шмидта, и тогда .
• Построение QR-разложения является основой QR-алгоритма ― одного из методов поиска собственных векторов и значений матрицы.
• Алгоритмы решения СЛАУ на основе QR-разложения практически одинаково работают как для хорошо обусловленных, так и для сингулярных систем .

Интерполяционное разложение

• Ограничения: произвольная матрица размерности и ранга .
• Вид разложения: , где — подмножество из индексов ; матрица состоит из соответствующих столбцов изначальной матрицы; матрица, все элементы которой по модулю не больше 2 (кроме того, содержит единичную подматрицу размерности ). Аналогичное разложение можно получить и по строкам.

Разложения, связанные с собственными или сингулярными значениями

Спектральное разложение матрицы

• Ограничения: диагонализуемая квадратная матрица , т. е. имеющая набор из различных собственных векторов (при этом собственным значениям не обязательно различаться).
• Вид разложения: , где — диагональная, образованная из собственных значений , а столбцы — соответствующие собственные вектора.
• Существование: матрица размерности всегда имеет собственных значений (с учетом кратности), которые могут быть упорядочены (не единственным способом), чтобы построить диагональную матрицу размерности и соответствующую матрицу из ненулевых столбцов , которые удовлетворяют равенству . Если собственных векторов различны, тогда матрица имеет обратную, что и даст искомое разложение −1 .
• Всегда можно нормировать собственные векторы, чтобы те имели длину 1. Если вещественная симметричная матрица, то всегда обратима и нормализуема. В этом случае матрица оказывается ортогональной, поскольку собственные векторы ортогональны по отношению друг к другу. Таким образом, искомое разложение (которое в рассматриваемом случае всегда существует) можно записать как .
• Необходимым и достаточным условием диагонализуемости является совпадение геометрической и алгебраической кратности каждого собственного значения. В частности, наличие различных собственных значений является достаточным (но не необходимым) условием.
• Спектральное разложение полезно для понимания решений систем линейных обыкновенных дифференциальных уравнений или разностных уравнений. Например, разностное уравнение с начальным условием имеет решение , что можно записать иначе как (в случае, если ). Возведение в степень диагональной матрицы сведется к возведению каждого элемента на диагонали в степень , что несравнимо проще, чем (если, конечно, последняя изначально не имеет диагональный вид).

Жорданова нормальная форма Жорданова матрица

• Ограничения: квадратная матрица .
• Вид разложения: , где — жорданова матрица, а — матрица перехода к новому базису.
• Жорданова нормальная форма является обобщением диагональной формы матрицы , составленной из собственных значений, на случай, когда геометрическая кратность одного или нескольких собственных значений меньше алгебраической кратности.

Разложение Шура

• Ограничения: квадратная матрица .
• Существует две версии разложения: для случая вещественной матрицы и для случая комплексной матрицы. Последняя всегда имеет комплексное разложение Шура.
• Вид разложения (вещественный случай): (все матрицы в обеих частях равенства составлены из строго вещественных значений). В этом случае — ортогональная матрица, а — квазитреугольная. Последняя называется вещественной формой Шура. Блоки на диагонали � либо размера 1×1 (в таком случае они представляют собой действительные собственные значения) или 2×2 (образуемые парой комплексно-сопряженных собственных чисел).
• Вид разложения (комплексный случай): , где — унитарная, — ее эрмитово-сопряженная, а — верхняя треугольная матрица, называемая комплексной формой Шура, которая содержит собственные значения на диагонали.

QZ-разложение Разложение Шура Обобщенное разложение Шура

• Ограничения: квадратные матрицы и .
• Существует две версии разложения: комплексная и действительная.
• Вид разложения (комплексный случай): , где и — унитарные матрицы, — эрмитово-сопряженная к , и — верхне-треугольные матрицы.
• В указанном разложении соотношение диагональных элементов в и соответствующих в , являются обобщенными собственными значениями, которые являются решением обобщенной задачи поиска собственных значений (где — неизвестный скаляр и — неизвестный ненулевой вектор).
• Вид разложения (вещественный случай): , где все матрицы состоят строго из вещественных значений. — ортогональные матрицы, а — квазитреугольные, состоящие из блоков 1×1 или 2×2 (аналогичных соответствующим блокам в разложении Шура).

сингулярное разложение

• Ограничения: произвольная матрица размера .
• Вид разложения: , где Σ — неотрицательная диагональная матрица, — унитарные матрицы, а — эрмитово-сопряженная. В вещественном случае , причем Σ, как и прежде, неотрицательная диагональная матрица, — ортогональные .
• Элементы на диагонали матрицы Σ называются сингулярными значениями матрицы и обозначаются . Число ненулевых сингулярных значений матрицы равно рангу этой матрицы .
• Сингулярное разложение, как и спектральное разложение, включает в себя отыскание базиса подпространств, действие на элементы которых оператора эквивалентны умножению на скаляр (т. е. ), но при этом сингулярное разложение является более общим методом, поскольку матрица не обязана быть квадратной.

Другие разложения

Полярное разложение

• Ограничения: квадратная комплексная матрица .
• Вид разложения (комплексный случай): , где — эрмитова матрица с неотрицательными ведущими минорами, а — унитарная матрица.
• Вид разложения (вещественный случай): , где � — симметричная матрица с неотрицательными ведущими минорами, а — ортогональная матрица.
• Для невырожденной матрицы полярное разложение единственно, а для вырожденной матрицы однозначно определен лишь множитель .
• Полярное разложение матрицы в комплексном случае является аналогом представления произвольного комплексного числа в виде .

Фробениусова нормальная форма

• Ограничения: квадратная матрица .
• Вид разложения:, где — блочно-диагональная матрица, состоящая из сопровождающих матриц для унитарных многочленов таких, что кратен . — переходная матрица.

Вау!! 😲 Ты еще не читал? Это зря!

• Разделение матрицы
• Неотрицательная матричная факторизация
• Анализ главных компонентов

Исследование, описанное в статье про разложение матрицы, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое разложение матрицы, lu-разложение , разложение холецкого , сингулярное разложение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Линейная алгебра и аналитическая геометрия