2.8. Скалярное произведение векторов и его свойства

Скалярным произведением векторов a, b называется число ,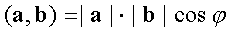
где φ - угол между векторами a, b.

Скалярное произведение обладает свойствами:

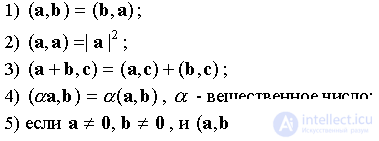
скалярное произведение векторов равно произведению |

Скаля́рное произведе́ние (иногда называемое внутренним произведением) — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат. Используется в определении длины векторов и угла между ними.

Обычно для скалярного произведения векторов и используется одно из следующих обозначений.

или просто

и второе обозначение применяется в квантовой механике для векторов состояния.

В простейшем случае, а именно в случае конечномерного вещественного евклидового пространства, иногда используют «геометрическое» определение скалярного произведения ненулевых векторов и как произведения длин этих векторов на косинус угла между ними:

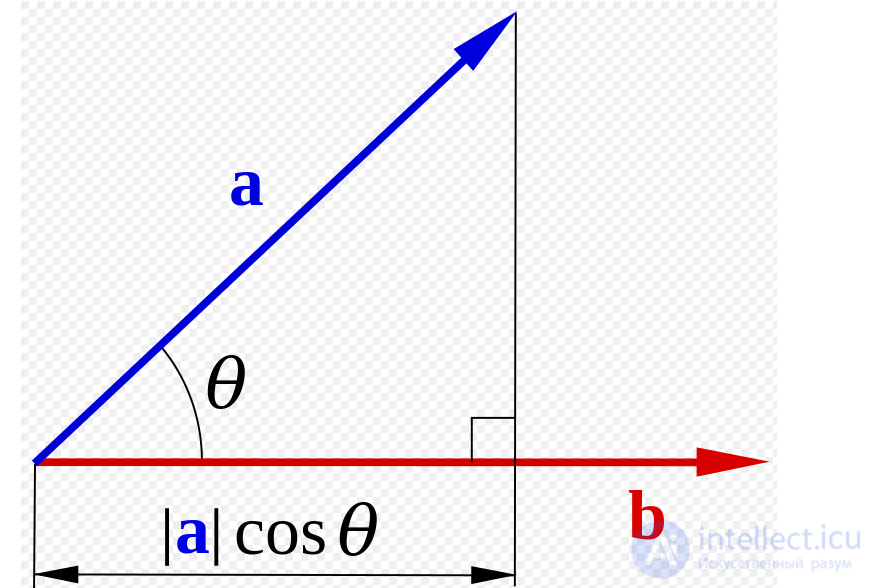
Равносильное определение: скалярное произведение есть произведение длины проекции первого вектора на второй и длины второго вектора (см. рисунок). Если хотя бы один из векторов нулевой, то произведение считается равным нулю.

У понятия скалярного произведения существует также большое количество обобщений для различных векторных пространств, то есть для множеств векторов с операциями сложения и умножения на скаляры. Данное выше геометрическое определение скалярного произведения предполагает предварительное определение понятий длины вектора и угла между ними. В современной математике используется обратный подход: аксиоматически определяется скалярное произведение, а уже через него — длины и углы. В частности, скалярное произведение определяется для комплексных векторов, многомерных и бесконечномерных пространств, в тензорной алгебре.

Скалярное произведение и его обобщения играют чрезвычайно большую роль в векторной алгебре, теории многообразий, механике и физике. Например, работа силы при механическом перемещении равна скалярному произведению вектора силы на вектор перемещения.

Определение и свойства

Будем говорить, что в вещественном или комплексном векторном пространстве определено скалярное произведение, если каждой паре векторов из поставлено в соответствие число из того числового поля, над которым задано �, удовлетворяющее следующим аксиомам.

1. Для любых трех элементов пространства и любых чисел справедливо равенство: (линейность скалярного произведения по первому аргументу).
2. Для любых справедливо равенство, где черта означает комплексное сопряжение.
3. Для любого имеем:, причем только при (положительная определенность и невырожденность скалярного произведения соответственно).

Заметим, что из аксиомы 2 следует, что — вещественное число. Поэтому аксиома 3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения. Если аксиома 3 не выполняется, то произведение называется индефинитным или неопределенным.

Если не только при , то произведение называется квазискалярным.

Из данных аксиом получаются следующие свойства:

1. коммутативность для вещественных векторов:

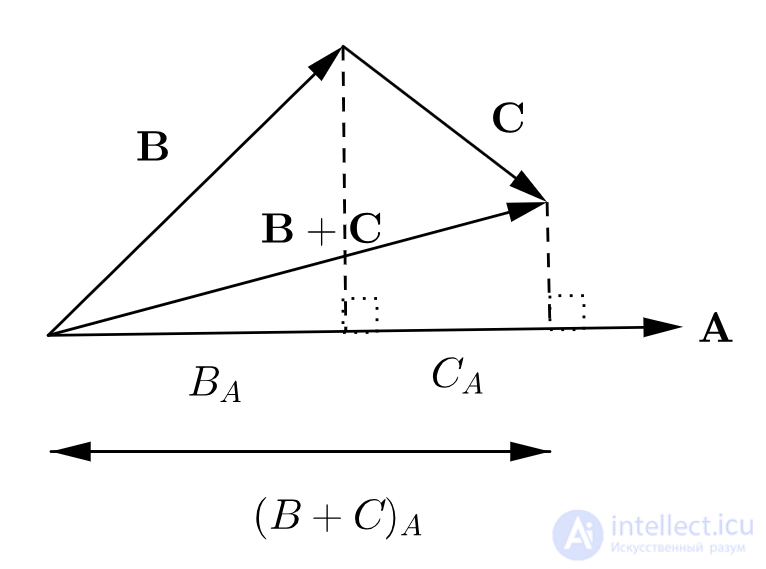
   Дистрибутивность скалярного произведения в случае вещественного евклидового пространства

2. дистрибутивность относительно сложения: и
3. инволюционная линейность относительно второго аргумента: (в случае вещественного — просто линейность по второму аргументу).
4. (что совпадает с для вещественного ).

Также есть свойства, связанные не с данными аксиомами:

1. неассоциативность относительно умножения на вектор': ;
2. ортогональность: два ненулевых вектора a и b ортогональны тогда и только тогда, когда (a, b) = 0 (определения ниже).

Замечание. В квантовой физике скалярное произведение (волновых функций, которые комплекснозначны) принято определять как линейное по второму аргументу (а не по первому), соответственно, по первому аргументу оно будет инволюционо линейным. Путаницы обычно не возникает, поскольку традиционное обозначение для скалярного произведения в квантовой физике также отличается: , т.е. аргументы отделяются вертикальной чертой, а не запятой, и скобки всегда угловые.

Определение и свойства в евклидовом пространстве

Вещественные векторы

В -мерном вещественном евклидовом пространстве векторы определяются своими координатами — наборами вещественных чисел в ортонормированном базисе. Определить скалярное произведение векторов можно так:

Проверка показывает, что все три аксиомы выполнены.

Например, скалярное произведение векторов (1,3,−5) и (4,−2,−1) будет вычислено так:

(

Можно доказать, что эта формула равносильна определению через проекции или через косинус:

Комплексные векторы

Для комплексных векторов определим аналогично:

Пример (для): (

Свойства

Помимо общих свойств скалярного произведения, для многомерных евклидовых векторов верно следующее:

1. в отличие от обычного умножения скаляров, где если ab = ac и a ≠ 0, то b равняется c, для скалярного умножения векторов это неверно: если a · b = a · c, то есть a · (b − c) = 0, то в общем случае a и b − c лишь ортогональны; но вектор b − c в общем случае не равен 0, то есть b ≠ c;
2. правило произведения: для дифференцируемых вектор-функций a(t) и b(t) верно соотношение (a(t), b(t))′ = a′(t) ⋅ b(t) + a(t) ⋅ b′(t);
3. оценка угла между векторами:

   в формуле знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение больше 0, если угол между векторами острый, и меньше 0, если угол между векторами тупой;

4. проекция вектора на направление, определяемое единичным вектором :

   , так как

5. площадь параллелограмма, натянутого на два вектора и , равна

Теорема косинусов в вещественном пространстве

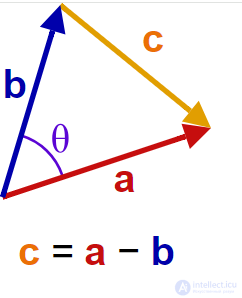
Теорема косинусов легко выводится с использованием скалярного произведения. Пусть на сторонах треугольника находятся векторы a, b и c, первые два из которых образуют угол θ, как показано в изображении справа. Тогда, следуя свойствам и определению скалярного произведения через косинус:

Связанные определения

В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия^[11]:

Длина вектора, под которой обычно понимается его евклидова норма:

(термин «длина» обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).

Углом между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):

Данные определения позволяют сохранить формулу: и в общем случае. Корректность формулы для косинуса гарантирует неравенство Коши — Буняковского^[12]:

Для любых элементов векторного пространства со скалярным произведением выполняется неравенство:

В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):

• Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определенным скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
• Пространство (вещественное или комплексное) с положительно определенным скалярным произведением называется предгильбертовым пространством.
  • При этом конечномерное вещественное пространство с положительно определенным скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
• Случай, когда скалярное произведение не является знакоопределенным, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.

История

Скалярное произведение было введено У. Гамильтоном в 1846 году одновременно с векторным произведением в связи с кватернионами — соответственно, как скалярная и векторная часть произведения двух кватернионов, скалярная часть которых равна нулю.

Вариации и обобщения

В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных или комплексных функций можно ввести положительно определенное скалярное произведение:

При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора:

При этом сама метрика (говоря точнее, ее представление в данном базисе) так связана со скалярными произведениями базисных векторов :

Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:

(

где К — положительно определенная, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определенное скалярное произведение).

Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свертка по повторяющимся индексам.

Применение

Скалярное произведение векторов находит широкое применение в различных областях математики, физики и инженерии. Вот несколько примеров его использования:

1. Геометрия:

   • Угол между векторами: Скалярное произведение используется для определения угла между двумя векторами. Формула a⋅b=∣a∣⋅∣b∣⋅cos(θ) позволяет найти косинус угла между векторами.

2. Физика:

   • Работа и энергия: В механике скалярное произведение применяется для определения работы приложенной силы по перемещению объекта. Работа равна скалярному произведению силы на смещение объекта.
   • Поток векторного поля: В электродинамике и гидродинамике скалярное произведение используется для определения потока векторного поля через поверхность.

3. Инженерия:

   • Сила и момент: В механике материалов скалярное произведение вектора силы и вектора радиуса применяется для определения момента силы относительно определенной точки.
   • Сигнальная обработка: В области обработки сигналов скалярное произведение может использоваться для измерения схожести или корреляции между двумя сигналами.

4. Графика и компьютерная графика:

   • Освещение и тени: В трехмерной графике скалярное произведение может использоваться для расчета освещения поверхности объектов, а также для создания эффектов теней.

5. Машинное обучение:

   • Анализ признаков: В машинном обучении скалярное произведение может применяться для анализа признаков и измерения схожести между векторами признаков.

6. Теория сигналов:

   • Кросс-корреляция: Скалярное произведение используется в кросс-корреляции сигналов для определения степени их схожести.

Эти примеры демонстрируют разнообразные области, в которых скалярное произведение векторов широко применяется для анализа и решения различных задач.

Вау!! 😲 Ты еще не читал? Это зря!

• Гильбертово пространство
• Векторное произведение
• Внешнее произведение
• Псевдоскалярное произведение
• Смешанное произведение