2.9. Векторное произведение векторов и его свойства

Привет, мой друг, тебе интересно узнать все про векторное произведение векторов, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое векторное произведение векторов, его свойства , настоятельно рекомендую прочитать все из категории Линейная алгебра и аналитическая геометрия.

Вектор c , удовлетворяющий условиям: 
  1)    
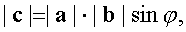
  2)    
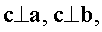
  3)   векторы a, b, c образуют правую тройку векторов - называется векторным произведением векторов и обозначается: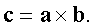   

Векторное произведение обладает свойствами:
  1)   ; 
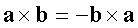  2)    ; 
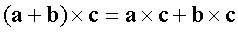  3) 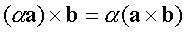  ;   α - вещественное число; 
  4) 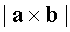    равен площади параллелограмма, построенного на векторах a, b ;
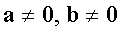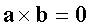  5)   если   ,   и   ,    то   .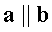 

Тебе нравиться векторное произведение векторов? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое векторное произведение векторов, его свойства и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Линейная алгебра и аналитическая геометрия