Прямое или декартово произведение двух множеств

Привет, сегодня поговорим про прямое или декартово произведение двух множеств, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое прямое или декартово произведение двух множеств , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Прямое или декартово произведение двух множеств — это множество, элементами которого являются всевозможные упорядоченные пары элементов исходных множеств.

Понятие прямого произведения естественно обобщается на произведение множеств с дополнительной структурой (алгебраической, топологическиой, и т. д.) поскольку произведение множеств часто наследует структуры, имевшиеся на исходных множествах.

 

 

Прямое произведение в теории множеств[править ]

Произведение двух множеств[править ]

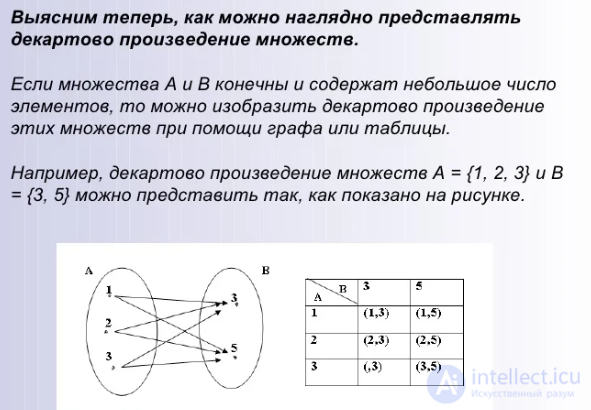
в	в	в	в	в	в	в	в
и	и	и	и	и	и	и	и
к	к	к	к	к	к	к	к
Произведение множества {в, и, к} на множество цветов радуги

Пусть даны два множества 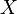 и 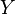. Прямое произведение множества  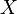и множества  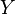есть такое множество 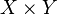, элементами которого являются упорядоченные пары  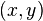для всевозможных  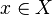и .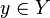

Отображения произведения множеств в его множител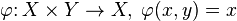и —  и 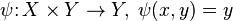 — называют координатными функциями.

Аналогично определяется произведение конечного семейства множеств.

Danger dungeon quest

Game: Perform tasks and rest cool.3 people play!

Play game

Комментарии[править ]

Строго говоря, тождество ассоциативности 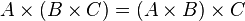 не имеет места, но в силу существования естественного взаимно однозначного соответствия между множествам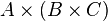и  и 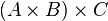 этим различием можно зачастую пренебречь.

Декартова степень[править ]

000	001	002	010	011	012	020	021	022
100	101	102	110	111	112	120	121	122
200	201	202	210	211	212	220	221	222
{0, 1, 2}3, 33 = 27 элементов

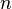-я Декартова степень множества  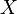определяется для целых неотрицательных 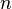, как 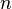-кратное Декартово произведение  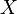на себя:

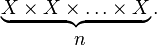
Обычно обозначается как 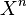 или .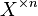

При положительных 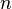 Декартова степень  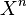состоит из всех упорядоченных наборов (кортежей) элементов из  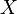длины 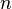. Так вещественное пространство 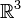(множество кортежей из трех вещественных чисел), есть 3 степень множества вещественных чисел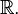 

При 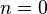, Декартова степень  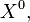по определению, содержит единственный элемент — пустой кортеж .

Прямое произведение семейства множеств[править ]

В общем случае, для произвольного семейства множеств (не обязательно различных) 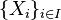 (множество индексов может быть бесконечным) прямое произведение  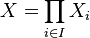определяется как множество функций, сопоставляющих каждому элементу  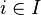элемент множества :

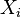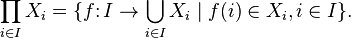
Отображения 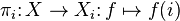  называются проекциями.

В частности, для конечного семейства множеств 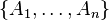 любая функция  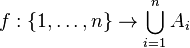 с условием  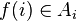эквивалентна некоторому кортежудлины 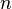, составленному из элементов множеств 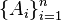, так, что на 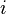-ом месте кортежа стоит элемент множества 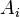. Об этом говорит сайт https://intellect.icu . Поэтому декартово (прямое) произведение конечного числа множеств  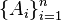может быть записано так:

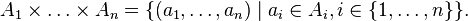
Проекции определяются следующим образом: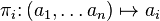 

Прямое произведение отображений[править ]

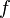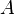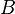Пусть  — отображение из  в , а 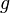 — отображение из  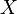в 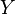. Их прямым произведением  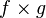называется отображение из  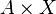в : .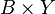

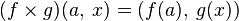Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.

Воздействие на математические структуры[править ]

Прямое произведение групп[править ]

Прямое (декартово) произведение двух групп 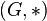 и 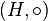 — это группа из всех пар элементов  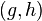с операцией покомпонентного умножения: 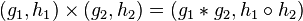. Эта группа обозначается как 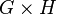. Ассоциативность операции умножения в группе  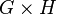следует из ассоциативности операций перемножаемых групп. Сомножител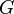и  и 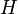 изоморфны двум нормальным подгруппам своего произведения,  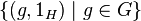и 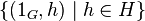 соответственно. Пересечение этих подгрупп состоит из одного элемента 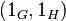, который является единицей группы-произведения. Координатные функции произведения групп являются гомоморфизмами.

Это определение распространяется на произвольное число перемножаемых групп. В случае конечного числа прямое произведение изоморфно прямой сумме. Отличие возникает при бесконечном числе множителей.

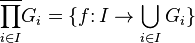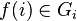В общем случае, , где  и 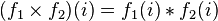. (Операция в правой части — это операция группы 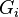.) Единицей группы-произведения будет последовательность, составленная из единиц всех перемножаемых групп: 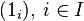. Например, для счетного числа групп: 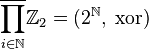, где в правой части стоит множество всех бесконечных двоичных последовательностей.

Подгруппа на множестве всех 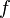, носитель которых (то есть множество 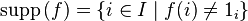) конечен, называется прямой суммой. Например, прямая сумма того же самого набора множеств  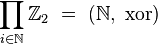содержит все двоичные последовательности с конечным числом единиц, а их можно трактовать какдвоичные  представления натуральных чисел.

Прямое произведение других алгебраических структур[править ]

Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причем в определении прямого произведения 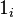(см. выше) следует заменить нулем. Определение произведения двух (или конечного числа) объектов совпадает с определением  прямой суммы. Однако, вообще говоря, прямая сумма отличается от прямого произведения: например, прямое произведение счетного множества копий  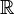суть пространство всехпоследовательностей действительных чисел, тогда как прямая сумма — пространство тех последовательностей, у которых только конечное число членов ненулевые (т. н. финитных последовательностей).

Прямое произведение топологических пространств[править ]

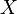Пусть  и 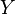 — два топологических пространства. Топология произведения  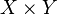задается базой, состоящей из всевозможных произведений 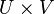, где 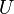 —открытое подмножество  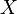и 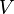 — открытое подмножество .

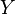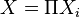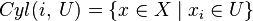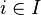Определение легко обобщается на случай произведения нескольких пространств. Для бесконечного произведения  определение усложняется. Определим открытый цилиндр , где  и 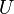 — открытое подмножество .

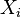Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество 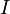 имеющим дискретную топологию).

Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений ее не удается доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).

Также, теорема  Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена  аксиома Колмогорова.

Прямое произведение графов[править ]

	—	
	—	
		
	—	

Множество вершин прямого произведения двух графов 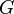 и 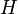 задается как произведение вершин графов сомножителей. Ребрами будут соединены следующие па́ры вершин:

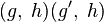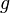• , где  и 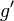 — соединенные ребром вершины граф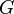а , а 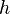 — произвольная вершина графа ;
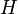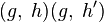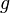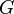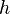• , где  — произвольная вершина графа , а  и 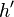 — соединенные ребром вершины графа .

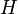Иначе говоря, множество ребер произведения графов является объединением двух произведений: ребер первого на вершины второго, и вершин первого на ребра второго.

Вариации и обобщения [править ]

Идея прямого произведения получила дальнейшее развитие в теории категорий, где она послужила основой для понятия произведения объектов. Неформально, произведение двух объектов 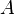 и 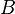 — это наиболее общий объект в данной категории, для которого существуют проекции на  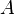и 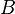. Во многих категориях (множеств, групп, графов, …) произведением объектов является именно их прямое произведение. Важно, что в большинстве случаев важно не столько конкретное определение прямого произведения, сколько указанное выше свойство универсальности. Различные определения будут давать при этом изоморфные  объекты .

Вау!! 😲 Ты еще не читал? Это зря![править ]

• Дизъюнктное объединение
• Полупрямое произведение
• Прямая сумма
• Тензорное произведение
• Декартовы координаты
• Операции над множествами
• Комбинаторика

 

 

//C#
using System;
using System.Collections.Generic;
using System.Text;

namespace mz
{
    class Program
    {
        static void Main(string[] args)
        {
            Console.WriteLine("Введите количество элементов в первом и втором множествах соответственно:");
            int xcount = Convert.ToInt32(Console.ReadLine());
            int ycount = Convert.ToInt32(Console.ReadLine());
            string[] X = new string[xcount];
            string[] Y = new string[ycount];
            Console.WriteLine("ВВедите элементы первого множества:");
            for (int i = 0; i < xcount; i++)
                X = Console.ReadLine();
            Console.WriteLine("ВВедите элементы второго множества:");
            for (int i = 0; i < ycount; i++)
                Y = Console.ReadLine();
            XY xy = new XY();
            string[] s = xy.MulXY(X, Y);
            Console.WriteLine("Результат:");
            xy.PrintMulXY(s);
            Console.ReadLine();
        }
    }
    public class XY
    {
        public string[] MulXY(string[] X, string[] Y)
        {
            string[] res = new string[X.Length * Y.Length];
            int k = 0;
            foreach (string i in X)
                foreach (string j in Y)
                {
                    res[k] = "(" + i + "," + j + ")";
                    k++;
                }
            return res;
        }
        public void PrintMulXY(string[] strMulXY)
        {
            foreach (string s in strMulXY)
                Console.WriteLine(" {0}", s);
            return;
        }
    }
}

 

 

На С++,с использованием STL.

Надеюсь, эта статья про прямое или декартово произведение двух множеств, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое прямое или декартово произведение двух множеств и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.