Лекция
Привет, сегодня поговорим про двоичное дерево, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое двоичное дерево , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Двои́чное де́рево — иерархическая структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.
Для практических целей обычно используют два подвида бинарных деревьев — двоичное дерево поиска и двоичная куча.
Существует следующее рекурсивное определение двоичного дерева (см. БНФ):
<дерево> ::= ( <данные> <дерево> <дерево> ) | nil .
То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). Об этом говорит сайт https://intellect.icu . Очевидным, но важным для понимания фактом является то, что каждое поддерево в свою очередь тоже является деревом. Если у некоторого узла оба поддерева пустые, то он называется листовым узлом (листовой вершиной) или терминальным элементом.
Например, показанное справа на рис. 1 дерево, согласно этой грамматике можно было бы записать так:
(m
(e
(c
(a nil nil)
nil
)
(g
nil
(k nil nil)
)
)
(s
(p (o nil nil) (s nil nil) )
(y nil nil)
)
)
|
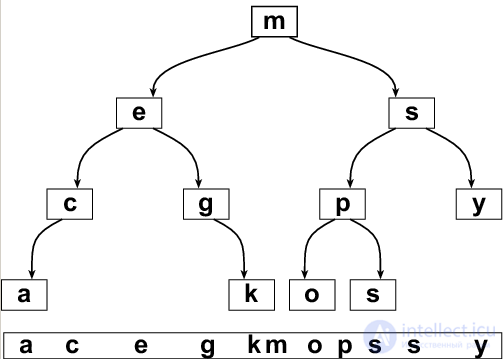
Рис. 1. Двоичное дерево поиска, в котором ключами являются латинские символы упорядоченные по алфавиту. |
Каждый узел в дереве задает поддерево, корнем которого он является. У вершины m=(data, left, right) есть два потомка (левый и правый) left и right и, соответственно, два поддерева (левое и правое) с корнями left и right.
Многие полезные структуры данных основаны на двоичном дереве:
Надеюсь, эта статья про двоичное дерево, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое двоичное дерево и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про двоичное дерево
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.