Лекция
Привет, сегодня поговорим про турнир теория графов , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое турнир теория графов , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
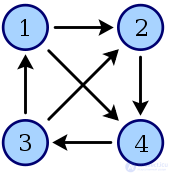
Турнир с 4 вершинами
вершин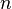 
ребер: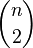 
Турнир – это ориентированный граф, полученный из неориентированного полного графа путем назначения направления каждому ребру. Таким образом, турнир – это орграф, в котором каждая пара вершин соединена одной направленной дугой.
Много важных свойств турниров были рассмотрены Ландау (Landau) [1] для того, чтобы исследовать модель доминирования цыплят в стае. Текущие приложения турниров включают исследования в области голосования и коллективного выбора[en] среди других прочих вещей. Имя турнир исходит из графической интерпретации исходов кругового турнира, в котором каждый игрок встречается в схватке с каждым другим игроком ровно раз, и в котором не может быть ничьих. В орграфе турнира вершины соответствуют игрокам. Дуга между каждой парой игроков ориентирована от выигравшего к проигравшему. Если игрок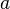 
побеждает игрока 
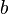, то говорят, что 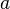доминирует над .
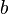Любой турнир с конечным числом 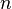вершин содержит гамильтонов путь, то есть ориентированный путь, содержащий все 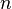вершин [2]. Это легко показать с помощьюматематической индукции по 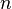: пусть утверждение верно для 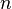, и пусть имеется некий турнир 
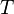с 
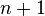вершинами. Выберем вершину 
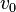в 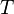и пусть 
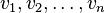– направленный путь в 
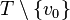. Пусть 
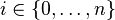- максимальное число, такое что для любого 
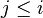имеется дуга из 
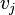в 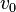. Путь
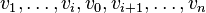
– искомый ориентированный путь. Это доказательство дает также алгоритм поиска гамильтонова пути. Известен более эффективный алгоритм, требующий перебора всего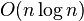 
дуг [3].
Это означает, что строго связный турнир имеет гамильтонов цикл [4] . Более строго: любой сильно связанный турнир является вершинно панциклическим[en] – для любой вершины v и для любого k от трех до числа вершин в турнире имеется цикл длины k, содержаший v.[5]. Более того, если турнир 4-связен, любая пара вершин может быть соединена гамильтоновым путем [6].
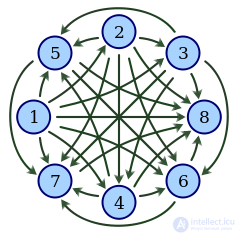
Транзитивный турнир с 8 вершинами.
Турнир, в котором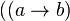 
и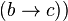 
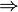
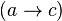, называется транзитивным. Об этом говорит сайт https://intellect.icu . В транзитивном турнире вершины могут быть полностью упорядочены в порядке достижимости[en].
Следующие утверждения для турнира с n вершинами эквивалентны:
Транзитивные турниры играют существенную роль в теории Рамсея, аналогичную роли, которую играют клики в неориентированных графах. В частности, любой турнир с n вершинами содержит транзитивный подтурнир с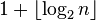 
вершинами.[7] Доказательство просто: выберем любую вершину v как часть этого подтурнира и построим подтурнир рекурсивно на множестве либо входящих соседей вершины v, либо на множестве исходящих соседей, в зависимости от того, какое множество больше. Например, любой турнир с семью вершинами содержит транзитивный турнир с тремя вершинами. Турнир Пейли с семью вершинами показывает, что это максимум, что можно гарантировать [7]. Однако Рейд и Паркер [8]показали, что эта граница не строга для некоторых больших значений числа n.
Эрдеш и Мозер [7] доказали, что существуют турниры с n вершинами без транзитивных подтурниров размера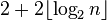 
. Их доказательство использует подсчет[en]: число вариантов в которых транзитивный турнир с k вершинами может содержаться в большем турнире с n помеченными вершинами, равно
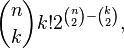
и при k превосходящем 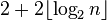это число слишком мало, чтобы транзитивный турнир оказался в каждом из 
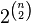различных турниров одного и того же множества из n помеченных вершин.
Игрок, выигравший все игры, естественно, будет победителем турнира. Однако, как показывает существование нетранзитивных турниров, такого игрока может не оказаться. Турнир, в котором каждый игрок проигрывает хотя бы одну игру называется 1-парадоксальным турниром. Обобщая, Турнир T=(V,E) называется k-парадоксальным, если для любого k-элементного подмножества S множества V существует вершина v0 в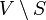 
, такая что 
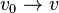для всех 
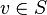. Посредствомвероятностного метода[en] Эрдеш показал, что для любого фиксированного k при условии |V| ≥ k22kln(2 + o(1)) почти любой турнир на V является k-парадоксальным.[9] С другой стороны, простой аргумент показывает, что любой k-парадоксальный турнир должен иметь по меньшей мере 2k+1 − 1 игроков, что было улучшено до(k + 2)2k−1 − 1 Эстер и Дьердьем Секерешами (1965) [10]. Существует явный метод построения k-парадоксальных турниров с k24k−1(1 + o(1)) игроками, разработанный Грэмом и Спенсером, а именно, турнир Пейли [11].
Конденсация любого турнира является транзитивным турниром. Таким образом, даже если турнир не является транзитивным, сильно связанные компоненты турнира могут быть полностью упорядочены.[12]
Последовательность счета турнира – это неубывающая последовательность полустепеней исхода вершин турнира. Множество счета турнира – это множество целых чисел, являющихся полустепенями исхода вершин турнира.
Теорема Ландау (1953) Неубывающая последовательность целых чисел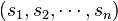 
является последовательностью счета тогда и только тогда, когда:
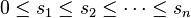
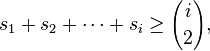для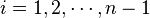 
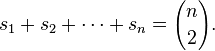
Пусть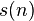 
– число различных последовательностей счета размера 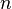. Последовательность 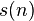начинается с:
1, 1, 1, 2, 4, 9, 22, 59, 167, 490, 1486, 4639, 14805, 48107, ...
(последовательность A000571 в OEIS)
Уинстон и Клейтман доказали, что для достаточно больших n
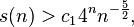
где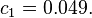 
Такач позже показал [13], используя некоторое правдоподобое, но недоказанное предположение, что
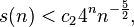
где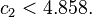 
Вместе это свидетельствует о том, что
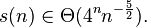
Здесь 
отражает асимптотически строгую границу.
Яо показал [14], что любое непустое множество неотрицательных целых чисел является множеством счета для некоторого турнира.
Надеюсь, эта статья про турнир теория графов , была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое турнир теория графов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.