Лекция
Привет, сегодня поговорим про отношение толерантности, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое отношение толерантности , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
Отношением толерантности (или просто толерантностью) на множестве 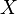 называется бинарное отношение, удовлетворяющее свойствам рефлексивности исимметричности, но не обязательно являющееся транзитивным. Таким образом, отношение эквивалентности является частным случаем толерантности.
называется бинарное отношение, удовлетворяющее свойствам рефлексивности исимметричности, но не обязательно являющееся транзитивным. Таким образом, отношение эквивалентности является частным случаем толерантности.
В отличие от отношения эквивалентности, дающего разбиение множества элементов, на котором оно определено, на непересекающиеся подмножества, отношение толерантности дает покрытие этого множества. Отношение толерантности используется, например, также при классификациях информации в базах знаний.
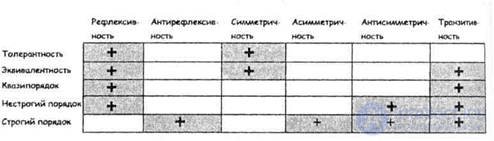
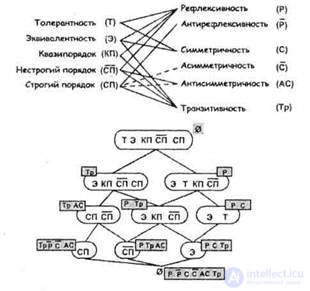
На содержательном уровне толерантность означает следующее. Любой объект неразличим сам с собой (свойство рефлексивности), а сходство двух объектов не зависит от того, в каком порядке они сравниваются (свойство симметричности). Однако, если один объект сходен с другим, а этот другой — с третьим, то это вовсе не значит, что все три объекта схожи между собой (таким образом, свойство транзитивности может не выполняться).
Отношение толерантности часто используется для описания отношения сходства между реальными объектами, отношений знакомства или дружбы между людьми. Об этом говорит сайт https://intellect.icu . Во всех этих случаях свойство транзитивности не предполагается обязательно быть выполненным. В самом деле, Иванов может быть знаком с Петровым, Петров — с Сидоровым, но при этом Иванов и Сидоров могут быть не знакомы между собой.
Толерантным также будет и отношение на множестве слов, при котором оно задается как наличие хотя бы одной общей буквы. В этом случае, например, в отношении находятся пересекающиеся слова кроссворда.
Рассмотрим примеры, где толерантность задается разными способами.
Пример1: Множество M состоит из четырехбуквенных русских слов - нарицательных существительных в именительном падеже. Будем называть такие слова сходными, если они отличаются не более чем на одну букву. Известная задача "Превращение мухи в слона" в точных терминах формулируется так. Найти последовательность слов, начинающуюся словом "муха" и кончающуюся словом "слон", любые два соседних слова в которой сходны в смысле только что данного определения. Решение этой задачи:
муха - мура - тура - тара - кара - каре - кафе - кафр - каюр - каюк - крюк - крок - срок - сток - стон - слон.
Пример. Множество M состоит из четырехбуквенных русских слов – нарицательных существительных в именительном падеже. Будем называть такие слова сходными, если они отличаются не более чем на одну букву. Известная задача "Превращение мухи в слона" в точных терминах формулируется так:
Найти такую последовательность слов, начинающуюся словом "муха" и кончающуюся словом "слон", любые два соседних слова в которой сходны (в смысле только что данного определения).
Приведем решение этой задачи: Муха – мура – тура – тара – кара – каре – кафе – кафр – каюр – каюк – крюк – крок – срок – сток – стон – слон.
На содержательном уровне толерантность означает следующее.Любой объект неразличим сам с собой (свойство рефлексивности), а сходство двух объектов не зависит от того, в каком порядке они сравниваются (свойство симметричности). Однако, если один объект сходен с другим, а этот другой — с третьим, то это вовсе не значит, что все три объекта схожи между собой (таким образом, свойство транзитивности может не выполняться).
Отношение толерантности часто используется для описания отношения сходства между реальными объектами, отношений знакомства или дружбы между людьми. Во всех этих случаях свойство транзитивности не предполагается обязательно быть выполненным. В самом деле, Иванов может быть знаком с Петровым, Петров — с Сидоровым, но при этом Иванов и Сидоров могут быть не знакомы между собой.
Надеюсь, эта статья про отношение толерантности, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое отношение толерантности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про отношение толерантности
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.