Общие свойства отношений кратко

Привет, сегодня поговорим про общие свойства отношений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое общие свойства отношений , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

Пусть А – бинарное отношение в множестве Х. Определим общие свойства таких отношений, которые должны выполняться для всех пар (Xi, Xj) Î A.

· Рефлексивность.

Отношение А рефлексивно, если А É Е (Е – тождественное отношение), т. е. оно всегда выполняется между объектом и им самим: Х А Х.

· Антирефлексивность.

Отношение А антирефлексивно, если А Е = 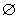, т. е. оно выполняется только для несовпадающих объектов: изXi А Xj следует, что Xi ¹ Xj (строгое неравенство; «быть старше»).

· Симметричность.

Отношение А симметрично, если А = А-1, т. Об этом говорит сайт https://intellect.icu . е. при выполнении соотношения Xi А Xj выполняется соотношениеXj А Xi («быть братом»).

· Асимметричность.

Отношение А асимметрично, если А А-1 = Æ, т. е. из двух соотношений Xi А Xj и Xj А Xi одно неверно («быть отцом»). Если отношение А асимметрично, то оно и антирефлексивно.

· Антисимметричность.

Отношение А антисимметрично, если А А-1 Ì Е, т. е. оба соотношения Xi А Xj и Xj А Xi выполняются одновременно только тогда, когда Xi = Xj.

· Транзитивность.

Отношение А транзитивно, если из соотношений Xi А Xj и Xj А Xk следует соотношение Xi А Xk («быть делителем»).

Для Рефлексивного Отношения все элементы матрицы на главной диагонали равны 1; для АнтирефлексивногоОтношения – это нули.

Симметричность отношения влечет за собой и симметричность матрицы; Асимметричность Отношения – несимметричность матрицы с нулевыми элементами на главной диагонали; Антисимметричность – только несимметричность матрицы.

В матрице Транзитивного отношения для каждой пары единичных элементов, один из которых расположен в I-м столбце и J-й строке, а другой – в J-м столбце и K-Й строке, обязательно существует единичный элемент, расположенный в I-м столбце и K-Й строке. Наличие единичных элементов на главной диагонали не нарушает транзитивности.

Надеюсь, эта статья про общие свойства отношений, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое общие свойства отношений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.