Функция SSCG Фридмана кратко

Привет, Вы узнаете о том , что такое sscg , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое sscg , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

В математике простой субкубический граф ( SSCG ) — это конечный простой граф, в котором каждая вершина имеет степень не более трех. Предположим, у нас есть последовательность простых субкубических графов. , , ... такой, что каждый графи имеет максимум вершины (для некоторого целого числа k) и для нет является гомеоморфно вкладывается в (т.е. является минором графа ) .

Теорема Робертсона –Сеймура доказывает, что субкубические графы (простые или нет) являются хорошо обоснованными в силу гомеоморфной вложимости, что подразумевает, что такая последовательность не может быть бесконечной. Затем, применяя лемму Кенига к дереву таких последовательностей при расширении, для каждого значения Существует последовательность максимальной длины. Функция SSCG(k) обозначает эту длину для простых субкубических графов. Функция SCG(k) обозначает эту длину для (общих) субкубических графов.

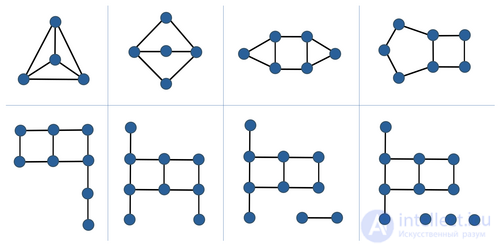
Последовательность субкубических графов.n -й граф в последовательности содержит не более n+3 вершин, и ни один граф не может быть гомеоморфно вложен в какой-либо более поздний граф в последовательности.SSCG⁡(3) определяется как максимально возможная длина такой последовательности.

Харви Фридман определил две функции: SSCG и SCG. Об этом говорит сайт https://intellect.icu . Он определил SSCG(к) как наибольшее целое число удовлетворяющий следующим условиям:

Есть последовательность G1,…,Gn простых субкубических графов, таких, что каждый имеет максимум вершины и для нет является гомеоморфно вкладывается в .

Первые несколько членов последовательности:

SSCG⁡(0)=2,

SSCG⁡(1)=5, и

SSCG⁡(2)=

[ 2 ]

Было показано, что следующий член SSCG(3) больше, чем TREE(3) .

Фридман показал, что SSCG(13) больше, чем время остановки любой машины Тьюринга , для которой можно доказать остановку за Π1
1-CA 0 с максимумом 2↑↑2000 символы, где↑↑ обозначает тетрацию . Он делает это, используя ту же идею, что и в случае .

Он также отмечает, что совершенно незаметен по сравнению с SSCG(13) .

Позже Фридман понял, что нет никаких оснований для требования «простоты» для субкубических графов. Он ослабляет это условие и определяет SCG(к) как самый большойнудовлетворяющий:

Есть последовательность субкубических графов, таких, что каждый имеет максимум вершины и для нет гомеоморфно вкладывается вГдж.

Первый член последовательности равен SCG(0)=6 , в то время как следующий срок SCG(1)больше числа Грэма . Более того,СКГ(3)больше, чем .

Адам П. Гаучер утверждает, что качественной разницы между асимптотическими темпами роста SSCG и SCG нет. Он пишет: «Очевидно, что SCG(n)≥SSCG(n) , но я также могу доказать SSCG(4n+3)≥SCG(n) ".

• Теорема Гудстейна
• Теорема Париса–Харрингтона
• Теорема Канамори–МакЭлуна
• Теорема Краскала о дереве , которая приводит к аналогичной функции TREE

Исследование, описанное в статье про sscg , подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое sscg и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.