Лекция
Привет, мой друг, тебе интересно узнать все про геометрический смысл определенного интеграла, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое геометрический смысл определенного интеграла , настоятельно рекомендую прочитать все из категории Математический анализ. Интегральное исчисление.
Пусть функция y = f(x) ≥ 0 непрерывна (и значит, интегрируема) на отрезке [a,b] (рис. 13). Интегральная сумма Sn при f(x) ≥ 0 равна площади фигуры, составленной из прямоугольников со сторонами f(ξi) · hi . Об этом говорит сайт https://intellect.icu . Следовательно, предел последовательности Sn при h → 0 равен площади S криволинейной трапеции, т.е. фигуры, ограниченной линией y = f(x) , осью ОХ и прямыми x = a, x = b : 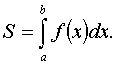
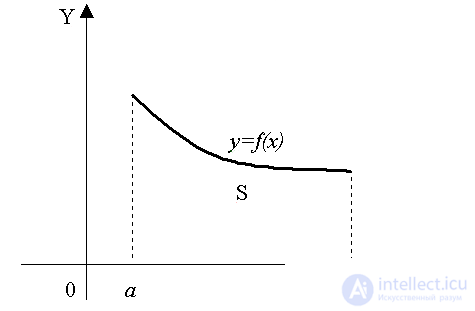
Рис. 13
Тебе нравиться геометрический смысл определенного интеграла? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое геометрический смысл определенного интеграла и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Интегральное исчисление
Из статьи мы узнали кратко, но содержательно про геометрический смысл определенного интеграла
Комментарии
Оставить комментарий
Математический анализ. Интегральное исчисление
Термины: Математический анализ. Интегральное исчисление