Интегралы. Историческая справка. Применение интегралов на практике примеры решения задач кратко

Привет, Вы узнаете о том , что такое интегралы, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое интегралы, применение интегралов , настоятельно рекомендую прочитать все из категории Математический анализ. Интегральное исчисление.

Имеется несколько типов интегралов: неопределенный и определенный интегралы , интеграл Римана и Римана-Стилтьеса, интеграл Лебега и Лебега-Стилтьеса, интеграл Даниэля. По области интегрирования интегралы подразделяются на кратные, криволинейные и поверхностные интегралы.Интеграл — одно из важнейших понятий математического анализа, которое возникает при решении задач о нахождении площади под кривой, пройденного пути при неравномерном движении, массы неоднородного тела, и тому подобных, а также в задаче о восстановлении функции по ее производной (неопределенный интеграл). Упрощенно интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых.

Историческая справка

Многие значительные достижения математиков Древней Греции в решении задач на нахождение площадей, атакже объемов тел связаны с именем Архимеда(287-212 до н. э.) Развивая идеи предшественников Архимед определил длину окружности и площадь круга, объем и поверхность шара. В работах «О шаре и цилиндре», «О спиралях», «О коноидах и сферах», он показал, что определение объемов шара, эллипсоида, гиперболоида и параболоида вращения сводится к определению объема конуса и цилиндра. Архимед разработал и применил методы, предвосхитившие созданное в XVII в. интегральное исчисление.

Потребовалось более полутора тысяч лет, прежде чем идеи Архимеда нашли четкое выражение и были доведены до уровня исчисления. В XVII в. математики
уже умели вычислять площади многих фигур с кривыми границами и объемы многих тел. А общая теория была создана во второй половине XVII в. в трудах великого английского математика Иссака Ньютона(1643-1716) и
великого немецкого математика Готфрида Лейбница(1646-1716). Ньютон и Лейбниц являются основателями интегрального исчисления. Они открыли важную теорему, носящую их имя: где f(x) – функция, интегрируемая на
отрезке [a;b], F(x) – одна из ее первообразных. Рассуждения, которые приводили Ньютон и Лейбниц, несовершенны с точки зрения современного математического анализа. В XVIII в. крупнейший представитель
математического анализа Леонард Эйлер эти понятия обобщил в своих трудах. Только в начале XIX в. были окончательно созданы понятия интегрального исчисления. Обычно при этом отмечают заслуги французского
математика Огюстена Коши и немецкого математика Георга Римана. Само слово интеграл придумал Я.Бернулли(1690г.). Оно происходит от латинского integro, которое переводится как приводить в прежнее
состояние, восстанавливать. В1696г. появилось и название новой ветви математики – интегральное исчисление, которое ввел И.Бернулли. Употребляющееся сейчас название первообразная функция заменило более раннее
«примитивная функция», которое ввел Лагранж (1797 г.). Обозначение определенного интеграла ввел Иосиф Бернулли, а нижние и верхние пределы Леонард Эйлер.

Основные понятия интегрального исчисления введены в работах Ньютона и Лейбница в конце XVII века. Лейбницу принадлежит обозначение интеграла 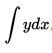, напоминающее об интегральной сумме, как и сам символ , от буквы 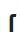(«длинная s») — первой буквы в латинском слове summa (тогда ſumma, сумма) . Сам термин «интеграл» предложен Иоганном Бернулли, учеником Лейбница. Обозначение пределов интегрирования в виде 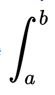введено Фурье в 1820 году.

Строгое определение интеграла для случая непрерывных функций сформулировано Коши в 1823 году, а для произвольных функций — Риманом в 1853 году. Определение интеграла в смысле Лебега впервые дано Лебегом в 1902 году (для случая функции одной переменной и меры Лебега).

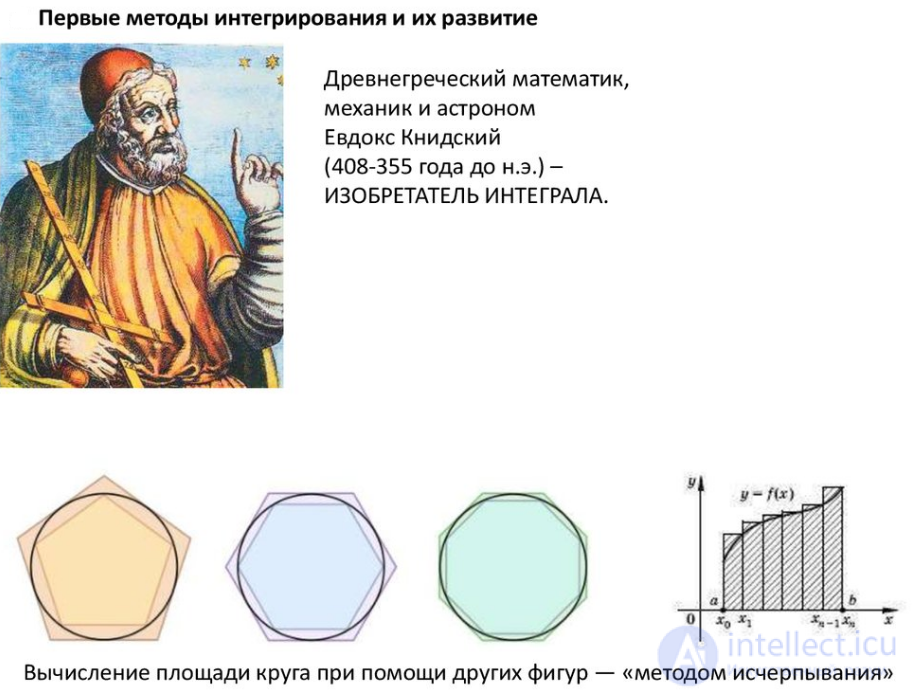
Интегрирование берет свое начало еще в древнем Египте примерно с 1800 года до н. э., о чем свидетельствует Московский математический папирус (или математический папирус Голенищева). Первым известным методом для расчета интегралов является метод для исследования площади или объема криволинейных фигур - метод исчерпывания Евдокса (Евдокс Книдский (ок. 408 г. до н.э. - ок. 355 г. до н.э.) - древнегреческий математик, механик и астроном), который был предложен примерно в 370 до н. э. Суть этого метода заключается в следующем: фигура, площадь или объем которой пытались найти, разбивалась на бесконечное множество частей, для которых площадь или объем уже известны. Об этом говорит сайт https://intellect.icu . Этот метод получил свое дальнейшее развитие в работах древнегреческого математика, физика и инженера Архимеда (287 до н.э. - 212 до н.э.) для расчета площадей парабол и приближенного расчета площади круга. Аналогичные методы были разработаны в Китае в третьем веке нашей эры китайским математиком Лю Хуэйем (ок. 220 - ок. 280), который с их помощью находил площадь круга. Для нахождения объема шара этот метод использовали китайский математик, астроном, механик, писатель Цзу Чунчжи (429 - 500) вместе со своим сыном, также математиком и астрономом, правителем области и государственным казначеем, Цзу Гэном.

Далее большой шаг вперед в развитии интегрального исчисления был предпринят в 11 веке в Ираке арабским ученым-универсалом, математиком, механиком, физиком и астрономом Абу Али аль-Хасан ибн аль-Хасан ибн аль-Хайсам аль-Басри (965-1039) (или Ибн ал-Хайсамом, в Европе известном как Alhazen), который в своей работе "Об измерении параболического тела" приводит формулы для суммы последовательных квадратов, кубов и четвертых степеней, и ряд других формул для сумм рядов. С помощью этих формул он проводит вычисление, равносильное вычислению определенного интеграла:

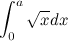
Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвертой степени. Таким образом, он был близок к поиску общей формулы для интегралов от полиномов не выше четвертой степени.

Следующий значительный толчок в исчислении интегралов состоялся лишь в 16 веке в работах итальянского математика Бонавентура Франческо Кавальери (1598 - 1647), в которых описывался предложенный им метод неделимых, а также в работах французского математика Пьера де Ферма (1601 - 1665). Этими учеными были заложены основы современного интегрального исчисления. Дальнейшее развитие связано с деятельностью английского математика, физика и богослова Исаака Барроу (1630 - 1677) и итальянского математика и физика, ученика Галилея Эванджелиста Торричелли (1608 - 1647), которые представили первые намеки на связь между интегрированием и дифференцированием.

За время становления интегрального исчисления менялось и обозначение интеграла. Английский физик, механик, математик и астроном Исаак Ньютон (1643 - 1727) использовал, правда не во всех своих работах, в качестве символа интегрирования значок квадрата перед обозначением функции или вокруг него, а также вертикальную черту над функцией, но эти обозначения не получили широкого распространения. Современное обозначение неопределенного интеграла было введено немецким философом, логиком, математиком, механиком, физиком, юристом, историком, дипломатом, изобретателем и языковедом Готфридом Вильгельмом Лейбницем (1646 - 1716) в 1675 году. Он образовал символ интеграла из буквы "длинная s" (от первой буквы слова Summa - сумма) Современное обозначение определенного интеграла, с указанием пределов интегрирования, было впервые предложено французским математиком и физиком Жаном Батистом Жозефом Фурье (1768 - 1830) в 1819-20 годах. Сам термин "интеграл" придумал швейцарский математик Якоб Бернулли (1654 - 1705) в 1690 году.

применение интегралов на практике

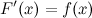Основной задачей дифференциального исчисления является определение для заданной функции ее производной или ее дифференциала 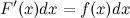. Обратная задача, состоящая в определении функции по ее известным производной 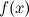или дифференциалу 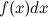, представляет собой основную задачу интегрального исчисления.

Применение определенного интеграла математике

1. Вычисление площади плоской фигуры в прямоугольных координатах.
2. Вычисление площади плоской фигуры в полярных координатах.
3. Вычисление объема тела вращения.
4. Вычисление длины дуги кривой.
5. Вычисление площади поверхности тела вращения. и т.д.

Применение определенного интеграла в физике

1. Работа А переменной силы.
2. S – (путь) перемещения пройденные телом.
3. Вычисление массы.
4. Вычисление момента инерции линии, круга, цилиндра.
5. Вычисление координаты центра тяжести.
6. Количество теплоты
7. Давление жидкости на вертикальную пластинку и т.д.

Применение определенного интеграла в биологии

1. Численность популяции.
2. Биомасса популяции.
3. Средняя длина пролета(пробега) животного и т.д.

Применение определенного интеграла в экономике

1. дисконтированной стоимости денежного потока
2. определение функции издержек
3. прогнозирование материальных затрат,
4. нахождение потребительского излишка
5. определение объема выпуска продукции,
6. определение экономической эффективности капитальных вложений (задача дисконтирования) и т.д.

л

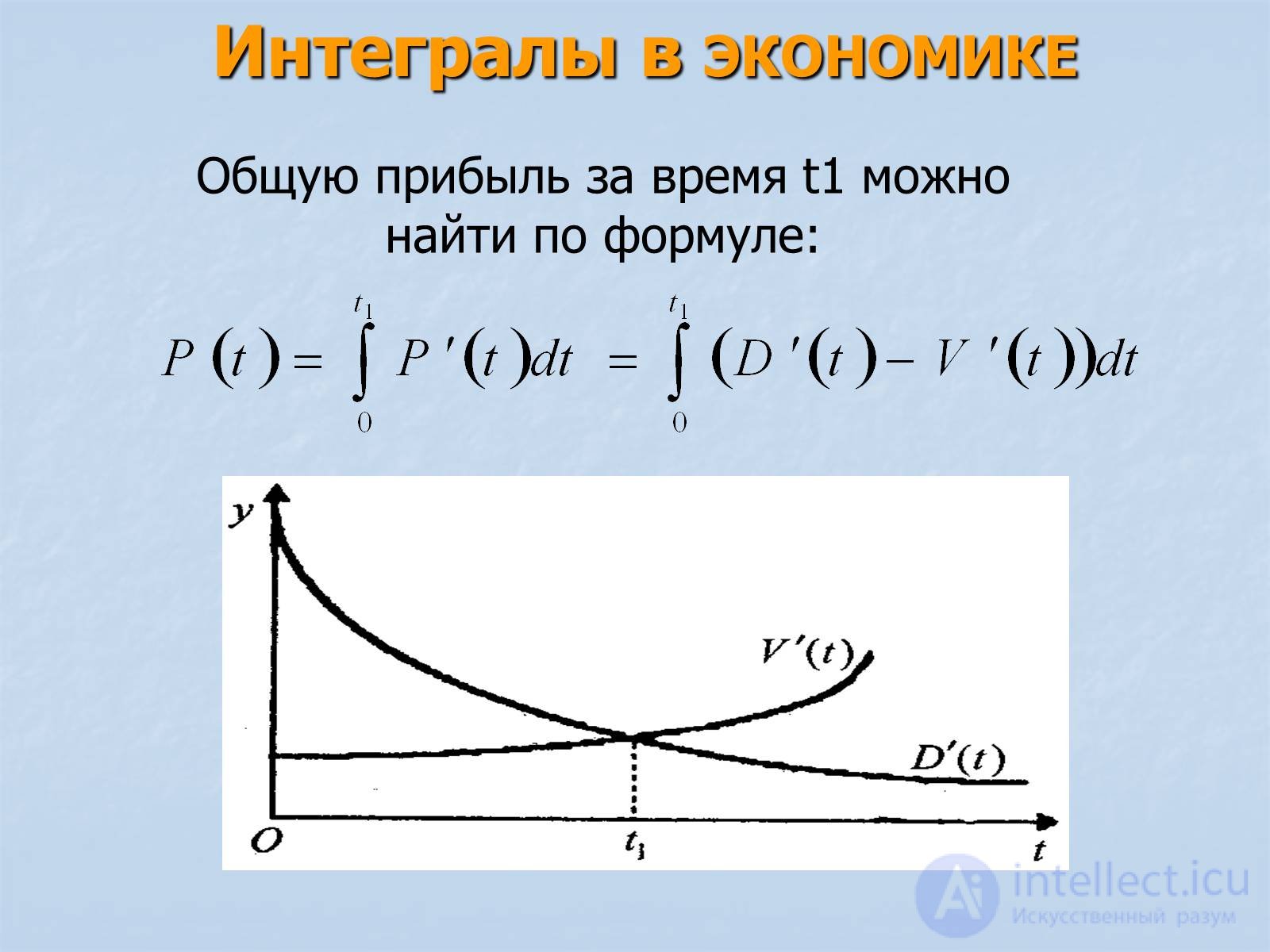
Интегралы в ЭКОНОМИКЕ
Общую прибыль за время t1 можно найти по формуле:

---

Интегралы в геометрии

Интегралы в геометрии

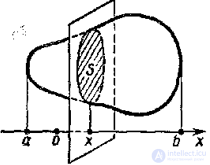
Пусть задано тело объемом V, причем имеется такая прямая, что, какую бы плоскость, перпендикулярную этой прямой, мы ни взяли, нам известна площадь S сечения тела этой плоскостью. Но плоскость, перпендикулярная оси Ох, пересекает ее в некоторой точке х. Следовательно, каждому числу х (из отрезка [а; b]) поставлено в соответствие единственное число S (х) — площадь сечения тела этой плоскостью. Тем самым на отрезке [а; b] задана функция S(x). Если функция S непрерывна на отрезке [а; b] то справедлива формула:

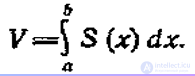
Интегралы в биологии
Средняя длина пути, который пролетают птицы, пересекая некоторую фиксированную область, вычисляется по формуле:

Интегралы в быту
Чтобы каша была вкусной, нужно такое отношение воды и круп:

1. Финансисты

---

Археологи

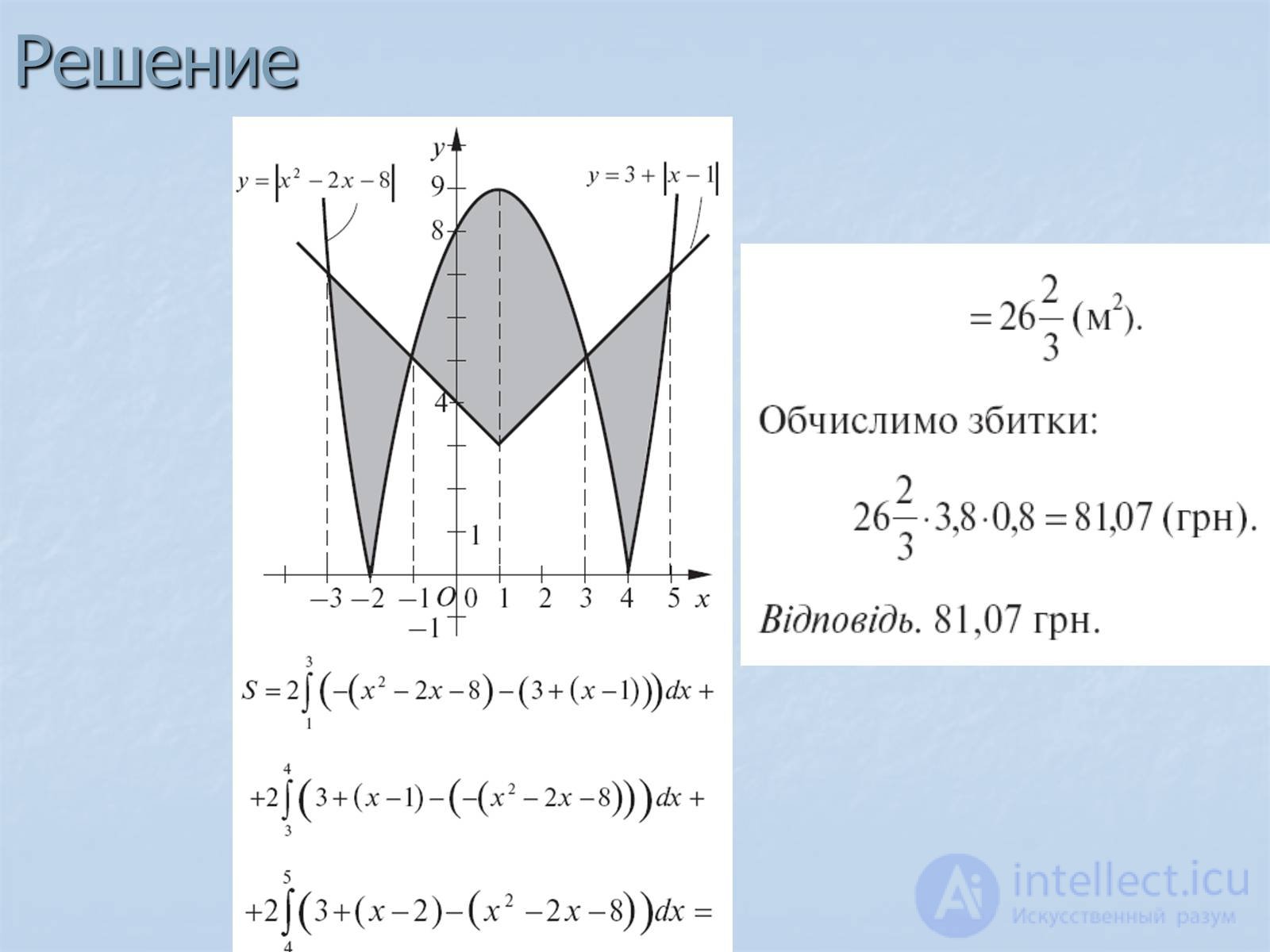
Решение

---

Физики

Решение

Биологи

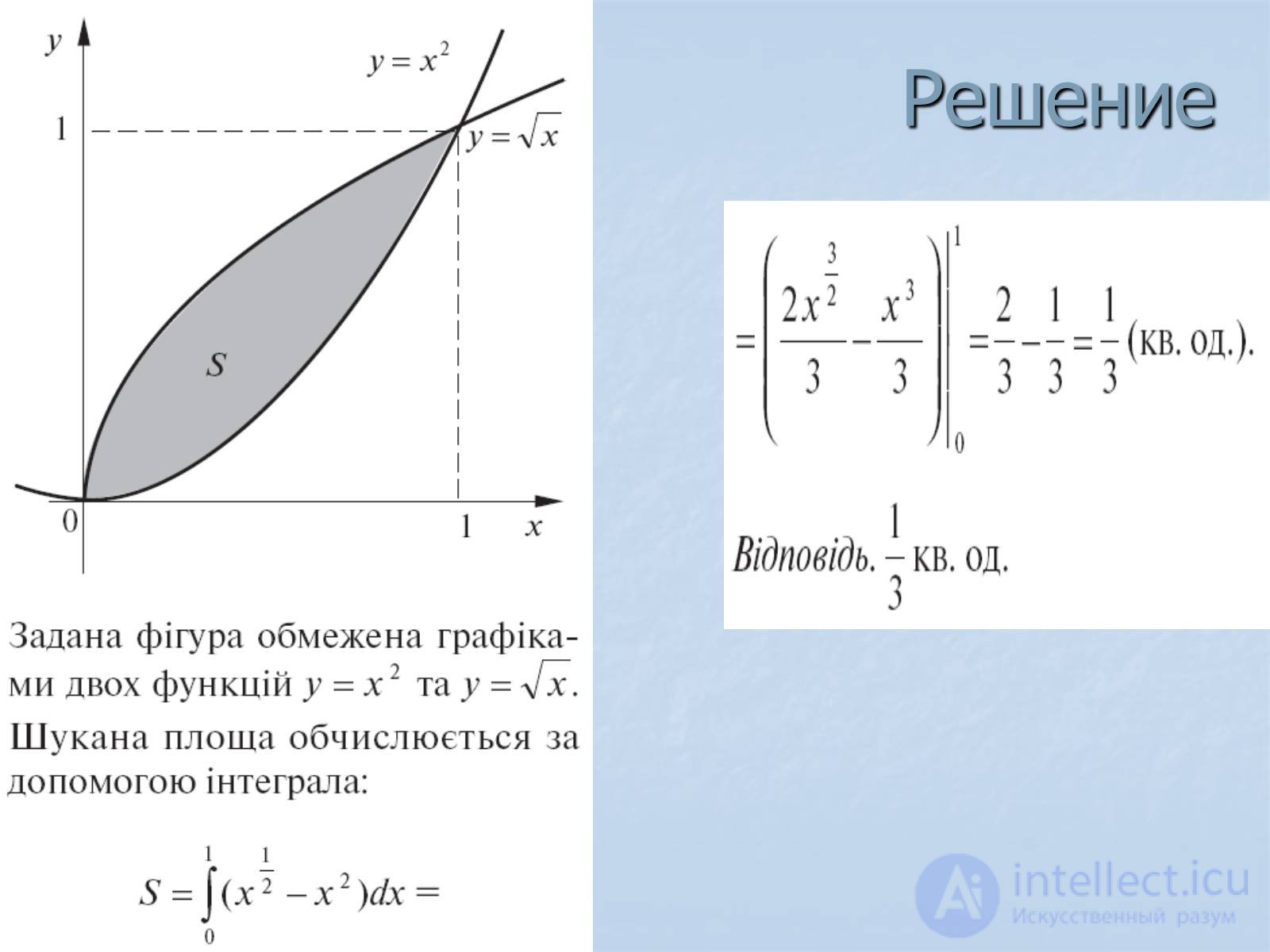
Решение

Энергетики

Анализ данных, представленных в статье про интегралы, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое интегралы, применение интегралов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Интегральное исчисление