3.4. Кратные интегралы и их приложения 3.4.1. Понятие двойного интеграла

Привет, мой друг, тебе интересно узнать все про кратные интегралы, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое кратные интегралы, их приложения понятие двойного интеграла , настоятельно рекомендую прочитать все из категории Математический анализ. Интегральное исчисление.

Пусть функция f(x,y) определена внутри некоторой области D и на ее границе. Разобьем область D на n частичных областей D₁, D₂, ..., D_n. Их площади обозначим черезσ₁, σ₂, ..., σ_n. Наибольшую хорду (отрезок, соединяющий две точки границы области) каждой из областей назовем ее диаметром. Через h обозначим диаметр, наибольший из всех n диаметров. В каждой частичной области возьмем по точке (P₁(x₁; y₁) в области D₁, P₂ (x₂; y₂) в области D₂ , и т.д.). Об этом говорит сайт https://intellect.icu . Составим интегральную сумму:

Устремим n к бесконечности так, чтобы h стремилось к нулю.

Конечный предел последовательности S_n (если он существует) при h → 0 , который не зависит ни от способа разбиения области D , ни от выбора точек P₁, P₂, ..., P_n, называется двойным интегралом функции f(x,y) и обозначается     .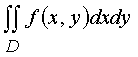

Функция f(x,y) называется интегрируемой функцией на области D . Область D называется областью интегрирования.

Непрерывная на замкнутой области функция является интегрируемой на этой области.

Тебе нравиться кратные интегралы? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое кратные интегралы, их приложения понятие двойного интеграла и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Интегральное исчисление