Лекция
Привет, сегодня поговорим про комплексный логарифм, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое комплексный логарифм , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).
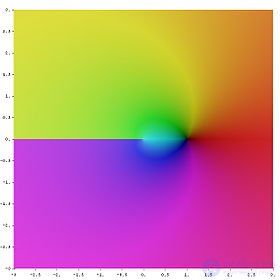
комплексный логарифм — аналитическая функция, получаемая распространением вещественного логарифма на всюкомплексную плоскость (кроме нуля). Существует несколько эквивалентных способов такого распространения. Данная функция имеет широкое применение в комплексном анализе. В отличие от вещественного случая, функция комплексного логарифма многозначна.
Для комплексных чисел логарифм можно определить так же, как для вещественных, то есть как обращениепоказательной функции. На практике используется практически только натуральный комплексный логарифм, основание которого — число Эйлера  : он обозначается обычно
: он обозначается обычно 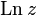 .
.
|
Натуральный логарифм комплексного числа |
Другие, эквивалентные данному, варианты определения приведены ниже.
В поле комплексных чисел решение этого уравнения, в отличие от вещественного случая, не определено однозначно. Например, согласно тождеству Эйлера, 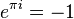 ; однако также
; однако также 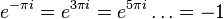 . Это связано с тем, что показательная функция вдоль мнимой оси является периодической (с периодом
. Это связано с тем, что показательная функция вдоль мнимой оси является периодической (с периодом 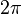 )[2], и одно и то же значение функция принимает бесконечно много раз. Таким образом, комплексная логарифмическая функция
)[2], и одно и то же значение функция принимает бесконечно много раз. Таким образом, комплексная логарифмическая функция 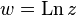 является многозначной.
является многозначной.
Комплексный нуль не имеет логарифма, поскольку комплексная экспонента не принимает нулевого значения. Ненулевое 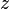 можно представить в показательной форме:
можно представить в показательной форме:
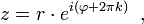 где
где 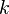 — произвольное целое число
— произвольное целое числоТогда 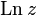 находится по формуле[3]:
находится по формуле[3]:
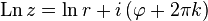
Здесь 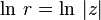 — вещественный логарифм. Отсюда вытекает:
— вещественный логарифм. Отсюда вытекает:
|
Комплексный логарифм |
Из формулы видно, что у одного и только одного из значений мнимая часть находится в интервале 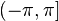 . Это значение называется главным значением комплексного натурального логарифма[1]. Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается
. Это значение называется главным значением комплексного натурального логарифма[1]. Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается 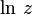 . Об этом говорит сайт https://intellect.icu . Иногда через
. Об этом говорит сайт https://intellect.icu . Иногда через 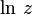 также обозначают значение логарифма, лежащее не на главной ветви. Если
также обозначают значение логарифма, лежащее не на главной ветви. Если 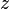 — вещественное число, то главное значение его логарифма совпадает с обычным вещественным логарифмом.
— вещественное число, то главное значение его логарифма совпадает с обычным вещественным логарифмом.
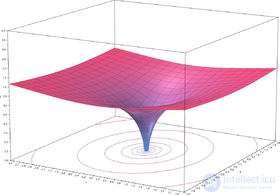
Из приведенной формулы также следует, что вещественная часть логарифма определяется следующим образом через компоненты аргумента:
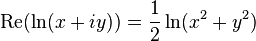
На рисунке показано, что вещественная часть как функция компонентов центрально-симметрична и зависит только от расстояния до начала координат. Она получается вращением графика вещественного логарифма вокруг вертикальной оси. С приближением к нулю функция стремится к 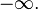
Логарифм отрицательного числа находится по формуле[3]:

Приведем главное значение логарифма (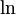 ) и общее его выражение (
) и общее его выражение (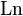 ) для некоторых аргументов:
) для некоторых аргументов:
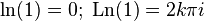

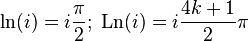
Следует быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:
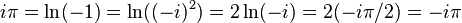 — явная ошибка.
— явная ошибка.Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви ( ). Причина ошибки — неосторожное использование свойства
). Причина ошибки — неосторожное использование свойства 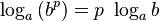 , которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.
, которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.
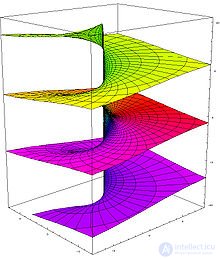
В комплексном анализе вместо рассмотрения многозначных функций на комплексной плоскости принято иное решение: рассматривать функцию как однозначную, но определенную не на плоскости, а на более сложном многообразии, которое называется римановой поверхностью[4]. Комплексная логарифмическая функция также относится к этой категории: ее образ (см. рисунок) состоит из бесконечного числа ветвей, закрученных в виде спирали. Эта поверхность непрерывна и односвязна. Единственный нуль у функции (первого порядка) получается при 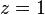 . Особые точки:
. Особые точки: 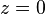 и
и 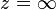 (точки разветвления бесконечного порядка)[5].
(точки разветвления бесконечного порядка)[5].
В силу односвязности риманова поверхность логарифма является универсальной накрывающей[6] для комплексной плоскости без точки 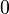 .
.
Логарифм комплексного числа также может быть определен как аналитическое продолжение вещественного логарифма на всюкомплексную плоскость. Пусть кривая 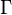 начинается в единице, не проходит через нуль и не пересекает отрицательную часть вещественной оси. Тогда главное значение логарифма в конечной точке
начинается в единице, не проходит через нуль и не пересекает отрицательную часть вещественной оси. Тогда главное значение логарифма в конечной точке 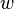 кривой
кривой 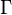 можно определить по формуле[5]:
можно определить по формуле[5]:
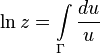
Если 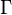 — простая кривая (без самопересечений), то для чисел, лежащих на ней, логарифмические тождества можно применять без опасений, например:
— простая кривая (без самопересечений), то для чисел, лежащих на ней, логарифмические тождества можно применять без опасений, например:
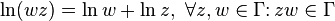
Главная ветвь логарифмической функции непрерывна и дифференцируема на всей комплексной плоскости, кроме отрицательной части вещественной оси, на которой мнимая часть скачком меняется на 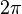 . Но этот факт есть следствие искусственного ограничения мнимой части главного значения интервалом
. Но этот факт есть следствие искусственного ограничения мнимой части главного значения интервалом 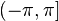 . Если рассмотреть все ветви функции, то непрерывность имеет место во всех точках, кроме нуля, где функция не определена. Если разрешить кривой
. Если рассмотреть все ветви функции, то непрерывность имеет место во всех точках, кроме нуля, где функция не определена. Если разрешить кривой 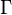 пересекать отрицательную часть вещественной оси, то первое такое пересечение переносит результат с ветви главного значения на соседнюю ветвь, а каждое следующее пересечение вызывает аналогичное смещение по ветвям логарифмической функции[5] (см. рисунок).
пересекать отрицательную часть вещественной оси, то первое такое пересечение переносит результат с ветви главного значения на соседнюю ветвь, а каждое следующее пересечение вызывает аналогичное смещение по ветвям логарифмической функции[5] (см. рисунок).
Из формулы аналитического продолжения следует, что на любой ветви логарифма[2]:
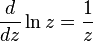
Для любой окружности 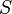 , охватывающей точку
, охватывающей точку 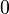 :
:
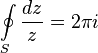
Интеграл берется в положительном направлении (против часовой стрелки). Это тождество лежит в основе теории вычетов.
Можно также определить аналитическое продолжение комплексного логарифма с помощью рядов, известных для вещественного случая:
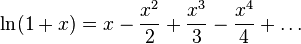 |
(Ряд 1) |
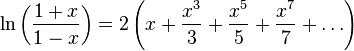 |
(Ряд 2) |
Однако из вида этих рядов следует, что в единице сумма ряда равна нулю, то есть ряд относится только к главной ветви многозначной функции комплексного логарифма. Радиус сходимости обоих рядов равен 1.
Поскольку комплексные тригонометрические функции связаны с экспонентой (формула Эйлера), то комплексный логарифм как обратная к экспоненте функция связан собратными тригонометрическими функциями[7] [8]:
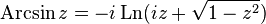
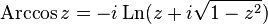
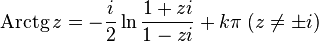

Гиперболические функции на комплексной плоскости можно рассматривать как тригонометрические функции мнимого аргумента, поэтому и здесь имеет место связь с логарифмом [8]:
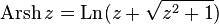 — обратный гиперболический синус
— обратный гиперболический синус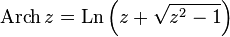 — обратный гиперболический косинус
— обратный гиперболический косинус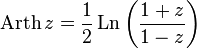 — обратный гиперболический тангенс
— обратный гиперболический тангенс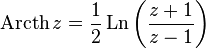 — обратный гиперболический котангенс
— обратный гиперболический котангенсПервые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда еще не было ясно определено само понятие логарифма[9]. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Д’Аламбером и Эйлером. Бернулли и Д’Аламбер считали, что следует определить 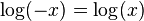 , в то время как Лейбниц доказывал, что логарифм отрицательного числа есть мнимое число[9]. Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной[10]. Хотя спор продолжался (Д’Аламбер отстаивал свою точку зрения и подробно аргументировал ее в статье своей «Энциклопедии» и в других трудах), подход Эйлера к концу XVIII века получил всеобщее признание.
, в то время как Лейбниц доказывал, что логарифм отрицательного числа есть мнимое число[9]. Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной[10]. Хотя спор продолжался (Д’Аламбер отстаивал свою точку зрения и подробно аргументировал ее в статье своей «Энциклопедии» и в других трудах), подход Эйлера к концу XVIII века получил всеобщее признание.
В XIX веке, с развитием комплексного анализа, исследование комплексного логарифма стимулировало новые открытия. Гаусс в 1811 году разработал полную теорию многозначности логарифмической функции[11], определяемой как интеграл от  . Риман, опираясь на уже известные факты об этой и аналогичных функциях, построил общую теорию римановых поверхностей.
. Риман, опираясь на уже известные факты об этой и аналогичных функциях, построил общую теорию римановых поверхностей.
Разработка теории конформных отображений показала, что меркаторская проекция в картографии, возникшая еще до открытия логарифмов (1550), может быть описана как комплексный логарифм[12].
На этом все! Теперь вы знаете все про комплексный логарифм, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое комплексный логарифм и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Из статьи мы узнали кратко, но содержательно про комплексный логарифм
Комментарии
Оставить комментарий
Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Термины: Комплексный анализ и операционное исчисление (теория функций комплексного переменного)