Лекция
Привет, Вы узнаете о том , что такое эллиптическая функция, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое эллиптическая функция , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).
эллиптическая функция — в комплексном анализе периодическая в двух направлениях функция, заданная на комплексной плоскости. Эллиптические функции можно рассматривать как аналоги тригонометрических (имеющих только один период). Исторически, эллиптические функции были открыты как функции, обратные эллиптическим интегралам.
Эллиптической функцией называют такую мероморфную функцию f , определенную на области , для которой существуют два ненулевых комплексных числа a и b , таких что
а также частное не является действительным числом.
Из этого следует, что для любых целых m и n
.
Любое комплексное число ω, такое что
называют периодом функции f. Если периоды a
и b
таковы, что любое ω
может быть записано как
то a и b называют фундаментальными периодами. Каждая эллиптическая функция обладает парой фундаментальных периодов.
Параллелограмм с вершинами в 0 , a , b , a+b называется фундаментальным параллелограммом.
где h, g — рациональные функции, — функция Вейерштрасса с теми же периодами, что и у f(z) . Если при этом f(z) является четной функцией, то ее можно представить в виде
, где h рациональна.
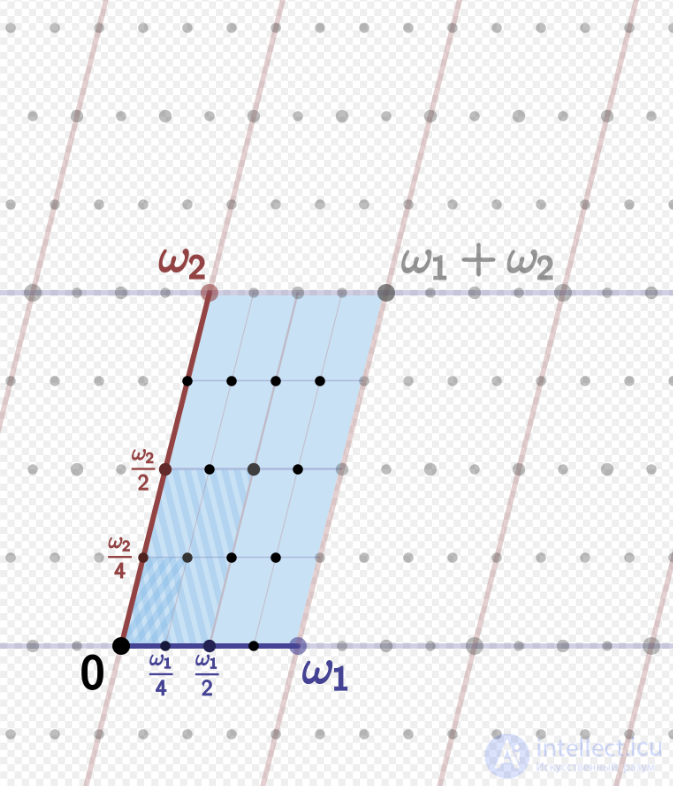
Фундаментальная область эллиптической функции как элементарная ячейка ее решетки периодов.

Параллелограмм, в котором определены противоположные стороны
Если является эллиптической функцией с периодамиω1,ω2 он также считает, что
для каждой линейной комбинации см,н∈З
.
Абелева группа
называется решеткой периодов .
Параллелограмм , созданный и
является фундаментальной областьюΛ действуя наС
.
Геометрически комплексная плоскость замощена параллелограммами. Все, что происходит в одной фундаментальной области, повторяется во всех остальных. Поэтому мы можем рассматривать эллиптические функции как функции с факторгруппой. С/Λкак их область определения. Эта факторгруппа, называемая эллиптической кривой , может быть представлена как параллелограмм, в котором противоположные стороны отождествлены, что топологически является тором .
Следующие три теоремы известны как теоремы Лиувилля (1847) .
Голоморфная эллиптическая функция постоянна.
Это исходная форма теоремы Лиувилля , которая может быть выведена из нее. Голоморфная эллиптическая функция ограничена, поскольку принимает все свои значения в фундаментальной области определения, которая компактна. Поэтому она постоянна по теореме Лиувилля.
Каждая эллиптическая функция имеет конечное число полюсов в и сумма его остатков равна нулю.
Из этой теоремы следует, что не существует эллиптической функции, не равной нулю и имеющей ровно один полюс первого порядка или ровно один нуль первого порядка в фундаментальной области.
Неконстантная эллиптическая функция принимает каждое значение одинаковое количество раз в подсчитано с кратностью.
Одной из важнейших эллиптических функций является функция Вейерштрасса -функция. Для заданного периода решетки
это определяется
Он построен таким образом, что в каждой точке решетки имеется полюс второго порядка. Член есть ли способ сделать ряд сходящимся.
℘является четной эллиптической функцией; то есть,
. Об этом говорит сайт https://intellect.icu .
Его производная
является нечетной функцией, т.е.℘′(−з)=−℘′(з).
Один из основных результатов теории эллиптических функций заключается в следующем: каждая эллиптическая функция относительно заданной решетки периодовΛможет быть выражена как рациональная функция в терминах
и ′
.
The℘-функция удовлетворяет дифференциальному уравнению
где и
константы, которые зависят отΛ
. Точнее,
и
, где
и
так называемые серии Эйзенштейна .
На алгебраическом языке поле эллиптических функций изоморфно полю
,
где изоморфизм отображает к
и
к
.


Связь с эллиптическими интегралами имеет преимущественно историческую подоплеку. Эллиптические интегралы изучались Лежандром , чьи работы были продолжены Нильсом Хенриком Абелем и Карлом Густавом Якоби .
Абель открыл эллиптические функции, взяв обратную функциюφэллиптической интегральной функции
.
Кроме того, он определил функции
и
.
После продолжения на комплексную плоскость они оказались двоякопериодическими и известны как эллиптические функции Абеля .
Эллиптические функции Якоби аналогичным образом получаются как обратные функции эллиптических интегралов.
Якоби рассмотрел интегральную функцию
и перевернул его:х=сн(ξ).сн
означает sinus amplitudinis и является названием новой функции. [ 11 ] Затем он ввел функции cosinus amplitudinis и delta amplitudinis , которые определяются следующим образом:
.
Только сделав этот шаг, Якоби смог доказать свою общую формулу преобразования эллиптических интегралов в 1827 году.
Вскоре после развития исчисления бесконечно малых итальянский математик Джулио ди Фаньяно и швейцарский математик Леонард Эйлер начали разрабатывать теорию эллиптических функций . При попытке вычислить длину дуги лемнискаты они столкнулись с задачами, связанными с интегралами, содержащими квадратный корень многочленов 3-й и 4-й степени. Было ясно, что эти так называемые эллиптические интегралы невозможно решить с помощью элементарных функций. Фаньяно обнаружил алгебраическую связь между эллиптическими интегралами, которую он опубликовал в 1750 году. Эйлер немедленно обобщил результаты Фаньяно и сформулировал свою алгебраическую теорему сложения для эллиптических интегралов.
За исключением комментария Ландена его идеи не были развиты до 1786 года, когда Лежандр опубликовал свою работу Mémoires sur les intégrations par arcs d'ellipse . Впоследствии Лежандр изучал эллиптические интегралы и назвал их эллиптическими функциями . Лежандр ввел тройную классификацию – три вида, – что было существенным упрощением довольно сложной теории того времени. Другие важные работы Лежандра: Mémoire sur les transcendantes elliptiques (1792), Exercices de calcul intégral (1811–1817), Traité des fonctions elliptiques (1825–1832). Работа Лежандра в основном оставалась нетронутой математиками до 1826 года.
Впоследствии Нильс Хенрик Абель и Карл Густав Якоби возобновили исследования и быстро получили новые результаты. Сначала они обратили эллиптическую интегральную функцию. По предложению Якоби в 1829 году эти обратные функции теперь называются эллиптическими функциями . Одной из важнейших работ Якоби является Fundamenta nova theoriae functionum ellipticarum , опубликованная в 1829 году Теорема сложения, найденная Эйлером, была сформулирована и доказана в общем виде Абелем в 1829 году. В те времена теория эллиптических функций и теория двоякопериодических функций считались разными теориями. Их объединили Брио и Буке в 1856 году. Гаусс открыл многие свойства эллиптических функций 30 годами ранее, но никогда ничего не публиковал по этой теме
Эллиптические функции — это важный раздел анализа, который имеет широкие практические применения в науке и технике. Ниже приведен обзор по основным направлениям, где они реально используются
а) Колебания и маятники
Реальное движение математического маятника описывается не синусом, а эллиптической функцией.
При больших амплитудах уравнение движения интегрируется через эллиптический интеграл первого рода.
б) Электричество и магнетизм
Поля токов в кольцевых и тороидальных системах (катушки, токовые петли) выражаются через эллиптические интегралы.
Расчет индуктивности колец, магнитных полей токовых петель и токов на поверхности проводников.
в) Оптика и волны
Распространение света в нелинейных средах и солитоны (стационарные волновые пакеты) описываются через функции Якоби — разновидность эллиптических функций.
В оптических решетках и кристаллах эллиптические функции описывают модуляцию интенсивности и фазы.
а) Решение нелинейных дифференциальных уравнений
Многие нелинейные уравнения (Кортевега — де Фриза, Дюффинга, Шредингера) допускают решения в виде эллиптических функций Якоби или Вейерштрасса.
б) Теория чисел и комплексный анализ
Эллиптические функции лежат в основе модульных форм, эллиптических кривых и теоремы Ферма (через доказательство Уайлса).
Используются в построении функций распределения и в криптографии.
Эллиптические кривые — это геометрические объекты, определяемые уравнениями вида
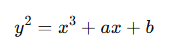
Их свойства напрямую связаны с эллиптическими функциями.
Применения:
Эллиптическая криптография (ECC) — современный стандарт шифрования (в TLS, биткойне, Ethereum и др.).
Электронная подпись, обмен ключами (ECDH), аутентификация.
Движение тела в центральном поле (например, планеты) при отклонении от круговой орбиты часто выражается через эллиптические интегралы.
Расчет орбит при возмущениях, траекторий космических аппаратов, прецессий.
Эллиптические функции позволяют аналитически описывать орбитальные параметры, где обычные тригонометрические приближения не подходят.
Фильтры Чебышева и эллиптические фильтры (в аналоговой и цифровой обработке сигналов) используют эллиптические функции для формирования нужных частотных характеристик.
Расчет переходных процессов в цепях с нелинейными элементами.
В описании поверхностей волны, вихрей и стоячих волн часто появляются решения через эллиптические функции (например, сверхтекучесть, поверхностные волны).
В графике и моделировании — для генерации периодических узоров с контролируемыми формами (в отличие от синуса).
В квантовых вычислениях и теории суперструн эллиптические функции описывают поведение волновых функций на торе.
| Область | Применение |
|---|---|
| Физика | Маятники, волны, поля, солитоны |
| Математика | Дифференциальные уравнения, теория чисел |
| Криптография | Шифрование на эллиптических кривых |
| Астрономия | Орбиты и гравитационные задачи |
| Электроника | Эллиптические фильтры |
| Гидродинамика | Поверхностные волны |
| Компьютерная графика | Генерация сложных периодических структур |
Исследование, описанное в статье про эллиптическая функция, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое эллиптическая функция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Комментарии
Оставить комментарий
Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Термины: Комплексный анализ и операционное исчисление (теория функций комплексного переменного)