Лекция
Привет, Вы узнаете о том , что такое сигнал, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое сигнал, аналоговый сигнал, цифровой сигнал, характеристики сигнала , настоятельно рекомендую прочитать все из категории МЕТРОЛОГИЯ И ЭЛЕКТРОРАДИОИЗМЕРЕНИЯ.
сигнал — материальное воплощение сообщения для использования при передаче, переработке и хранении информации.
Сигнал — код (символ, знак), созданный и переданный в пространство (по каналу связи) одной системой, либо возникший в процессе взаимодействия нескольких систем. Смысл и значение сигнала проявляются после регистрации и интерпретации в принимающей системе.
Сигнал (в теории информации и связи) — носитель информации, используемый для передачи сообщений в системе связи.
Любой сигнал может быть представлен в виде функции, которая описывает изменения его характеристик. Такое представление удобно для изучения устройств и систем радиотехники. Помимо сигнала в радиотехнике есть еще шум, который является его альтернативой. Шум не несет полезной информации и искажает сигнал, взаимодействуя с ним.
Существует немалое количество попыток сформулировать достаточно удобное определение этого термина и в специальной литературе , и в формальных нормативных актах.
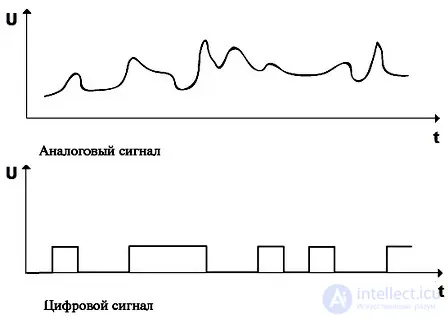
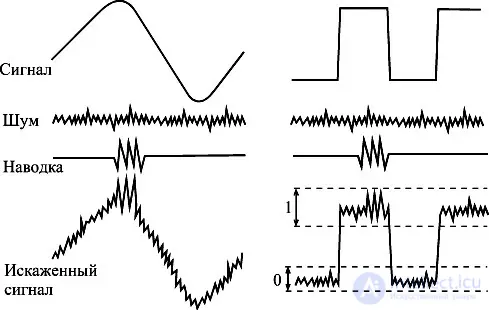
Рис идеальный и искаженный (реальный) цифровой и аналоговый сигнал
Помимо приведенного выше энциклопедического определения существует в классической литературе и множество иных вариантов определения термина «сигнал».
«Обычно под сигналом понимают величину, отражающую каким-либо образом состояние физической системы. В этом смысле естественно рассматривать сигнал как результат некоторых измерений, проводимых над физической системой в процессе ее наблюдения».
«Сигнал может быть определен как функция, переносящая информацию о состоянии или поведении физической системы. (...) Математически сигналы представляются в виде функций одной или нескольких независимых переменных».
«Сигнал — это изменяющаяся во времени физическая величина, описываемая функцией времени. Один из параметров этой функции содержит информацию о другой физической величине. Такой параметр сигнала (функции) называют информативным, а физическую величину, которой представлен сигнал, — носителем сигнала (несущей сигнала); сигнал имеет размерность этой величины».
«Сигналом обычно называют то, что несет в себе какие-то данные».
Сигнал может генерироваться, но его прием не обязателен, в отличие от сообщения, которое рассчитано на принятие принимающей стороной, иначе оно не является сообщением. Сигналом может быть любой физический процесс, параметры которого изменяются (или находятся) в соответствии с передаваемым сообщением.
Сигнал, детерминированный или случайный, описывают математической моделью, функцией, характеризующей изменение параметров сигнала. Математическая модель представления сигнала, как функции времени, является основополагающей концепцией теоретической радиотехники, оказавшейся плодотворной как для анализа, так и для синтеза радиотехнических устройств и систем. В радиотехнике альтернативой сигналу, который несет полезную информацию, является шум — обычно случайная функция времени, взаимодействующая (например, путем сложения) с сигналом и искажающая его. Основной задачей теоретической радиотехники является извлечение полезной информации из сигнала с обязательным учетом шума.
Понятие сигнал позволяет абстрагироваться от конкретной физической величины, например тока, напряжения, акустической волны и рассматривать вне физического контекста явления связанные кодированием информации и извлечением ее из сигналов, которые обычно искажены шумами. В исследованиях сигнал часто представляется функцией времени, параметры которой могут нести нужную информацию. Способ записи этой функции, а также способ записи мешающих шумов называют математической моделью сигнала.
В связи с понятием сигнала формулируются такие базовые принципы кибернетики, как понятие о пропускной способности канала связи, разработанное Клодом Шенноном и об оптимальном приеме, разработанная В. А. Котельниковым.
По физической природе носителя информации:
и другие;
По способу задания сигнала:
В зависимости от функции, описывающей параметры сигнала, выделяют :
Аналоговый сигнал
Аналоговый сигнал — сигнал данных, у которого каждый из представляющих параметров описывается функцией времени и непрерывным множеством возможных значений.
Большинство сигналов имеют непрерывную зависимость от независимой переменной (например, изменяются непрерывно во времени) и могут принимать любые значения на некотором интервале. «Сигналы в непрерывном времени и с непрерывным диапазоном амплитуд также называются аналоговыми сигналами». Аналоговые сигналы (АС) оказывается возможным описать некоторой непрерывной математической функцией времени.
Пример АС — гармонический сигнал: s(t) = A·cos(ω·t + φ).
Аналоговые сигналы используются в телефонии, радиовещании, телевидении. Ввести такой сигнал в цифровую систему для обработки невозможно, так как на любом интервале времени он может иметь бесконечное множество значений, и для точного (без погрешности) представления его значения требуются числа бесконечной разрядности. Поэтому очень часто необходимо преобразовывать аналоговый сигнал так, чтобы можно было представить его последовательностью чисел заданной разрядности.
Среди экспертов существует мнение, что термин «аналоговый сигнал» следует считать неудачным и устаревшим, а вместо него следует использовать термин «непрерывный сигнал».
Различают два пространства сигналов — пространство L (непрерывные сигналы), и пространство l (L малое) — пространство последовательностей.
Пространство l (L малое) есть пространство коэффициентов Фурье (счетного набора чисел, определяющих непрерывную функцию на конечном интервале области определения), пространство L — есть пространство непрерывных по области определения (аналоговых) сигналов.
При некоторых условиях, пространство L однозначно отображается в пространство l (например, первые две теоремы дискретизации Котельникова).
Аналоговые сигналы описываются непрерывными функциями времени, поэтому аналоговый сигнал иногда называют континуальным сигналом. Аналоговым сигналам противопоставляются дискретные (квантованные, цифровые). Примеры непрерывных пространств и соответствующих физических величин:
Свойства аналоговых сигналов в значительной мере являются противоположностью свойств квантованных или цифровых сигналов.
Аналоговые сигналы часто используют для представления непрерывно изменяющихся физических величин. Например, аналоговый электрический сигнал, снимаемый с термопары, несет информацию об изменении температуры, сигнал с микрофона — о быстрых изменениях давления в звуковой волне, и т. п.
Аналоговое телевидение — один из видов телевещания. В некоторых странах, например, в России [комм 1], эфирное аналоговое телевидение заменяется цифровым.
Дискретный сигнал
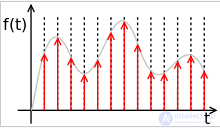
«Дискретные сигналы (сигналы в дискретном времени) определяются в дискретные моменты времени и представляются последовательностью чисел».
Дискретизация аналогового сигнала состоит в том, что сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени ti (где i — индекс). Об этом говорит сайт https://intellect.icu . Обычно промежутки времени между последовательными отсчетами (Δti = ti − ti−1) постоянны; в таком случае, Δt называется интервалом дискретизации. Сами же значения сигнала x(t) в моменты измерения, то есть xi = x(ti), называются отсчетами.
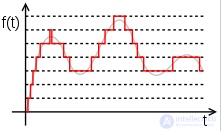
Квантованный сигнал
При квантовании вся область значений сигнала разбивается на уровни, количество которых должно быть представлено в числах заданной разрядности. Расстояния между этими уровнями называется шагом квантования Δ. Число этих уровней равно N (от 0 до N−1). Каждому уровню присваивается некоторое число. Отсчеты сигнала сравниваются с уровнями квантования и в качестве сигнала выбирается число, соответствующее некоторому уровню квантования. Каждый уровень квантования кодируется двоичным числом с n разрядами. Число уровней квантования N и число разрядов n двоичных чисел, кодирующих эти уровни, связаны соотношением n ≥ log2(N).
В соответствии с ГОСТ 26.013-81 , такие сигналы обозначены термином «многоуровневый сигнал».
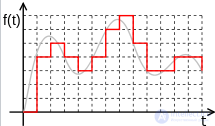
цифровой сигнал
К цифровым сигналам относят те, у которых дискретны как независимая переменная (например, время), так и уровень. Цифровой сигнал — сигнал, который можно представить в виде последовательности дискретных (цифровых) значений. В наше время наиболее распространены двоичные цифровые сигналы (битовый поток) в связи с простотой кодирования и используемостью в двоичной электронике. Для передачи цифрового сигнала по аналоговым каналам (например, электрическим или радиоканалам) используются различные виды манипуляции (модуляции).
Для того, чтобы представить аналоговый сигнал последовательностью чисел конечной разрядности, его следует сначала превратить в дискретный сигнал, а затем подвергнуть квантованию. Квантование является частным случаем дискретизации, когда дискретизация происходит по одинаковой величине, называемой квантом. В результате сигнал будет представлен таким образом, что на каждом заданном промежутке времени известно приближенное (квантованное) значение сигнала, которое можно записать целым числом. Последовательность таких чисел и будет являться цифровым сигналом.
Важным свойством цифрового сигнала, определившего его доминирование в современных системах связи, является его способность к полной регенерации в ретрансляторе (до некоторого порогового отношения сигнал/шум). Когда в ретранслятор приходит сигнал с небольшими помехами, он преобразуется в цифровую форму, и ретранслятор заново формирует сигнал, полностью убирая искажения. Аналоговый же сигнал удается усилить лишь вместе с наложившимися на него шумами.
С другой стороны, если цифровой сигнал приходит с большими помехами, восстановить его невозможно (эффект крутой скалы (англ.)), в то время как из искаженного аналогового сигнала можно извлечь часть информации, хотя и с трудом. Если сравнивать сотовую связь аналогового формата (AMPS, NMT) с цифровой связью (GSM, CDMA), то при помехах на цифровой линии из разговора выпадают порой целые слова, а на аналоговой можно вести разговор, хотя и с помехами.
Выход из данной ситуации — чаще регенерировать цифровой сигнал, вставляя регенераторы в разрыв линии связи, или уменьшать длину линии связи (например, уменьшать расстояние от сотового телефона до базовой станции, что достигается более частым расположением базовых станций на местности).
Использование в цифровых системах алгоритмов проверки и восстановления цифровой информации позволяет существенно увеличить надежность передачи информации.
определяет интервал времени, в течение которого сигнал существует (отличен от нуля);
— полоса частот, в пределах которой сосредоточена основная энергия сигнала;
. Необходимо отметить, что между шириной спектра и длительностью сигнала существует обратно пропорциональная зависимость: чем короче спектр, тем больше длительность сигнала. Таким образом, величина базы остается практически неизменной;
Параметры периодического импульсного сигнала:
амплитуда Uт – наибольшее из мгновенных значений (за период повторения Т);
период повторения Т – временной интервал от любого мгновенного значения сигнала до следующего мгновенного значения сигнала того же уровня (при одном значении производной);
частота повторения f – количество периодов колебаний за 1с;
длительность импульса и – временной интервал на уровне 0.5Um;
передний фронт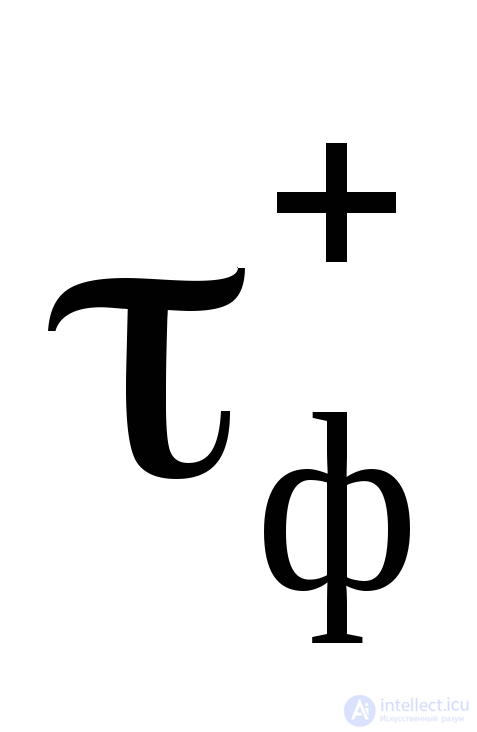 
– временной интервал, в течение которого сигнал увеличивается от уровня 0,1Um до уровня 0,9 Um;
задний фронт (срез)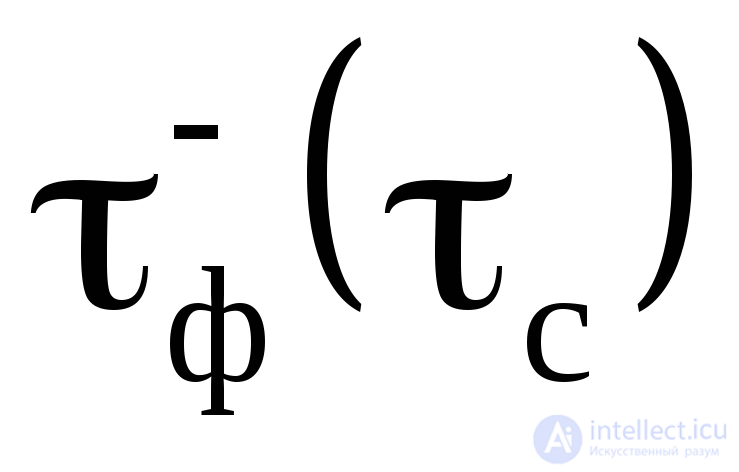 
– временной интервал, в течение которого сигнал уменьшается от уровня 0,9Um до уровня 0,1 Um;
Иногда длительность импульса указывают на некотором заданном уровне, например, на уровне 0,1Um –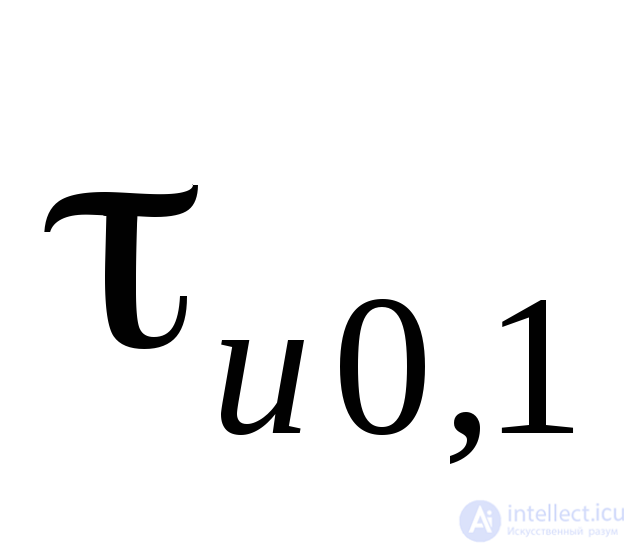 
.
Импульсный сигнал считают прямоугольным, если длительность плоской части на уровне Um составляет более трех длительностей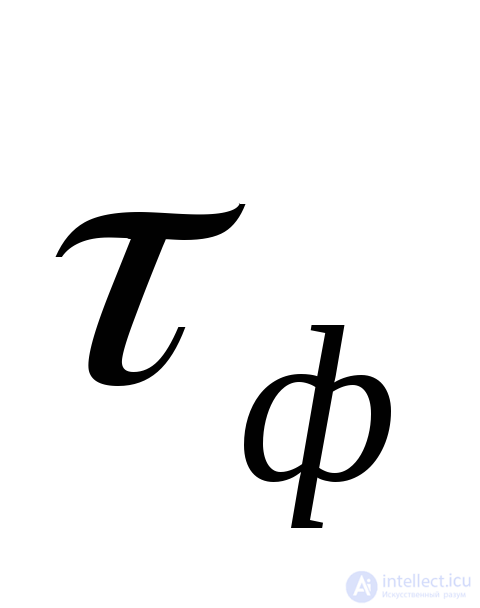 
.
На рис. 1.14 изображен периодически повторяющийся импульсный сигнал положительной полярности.
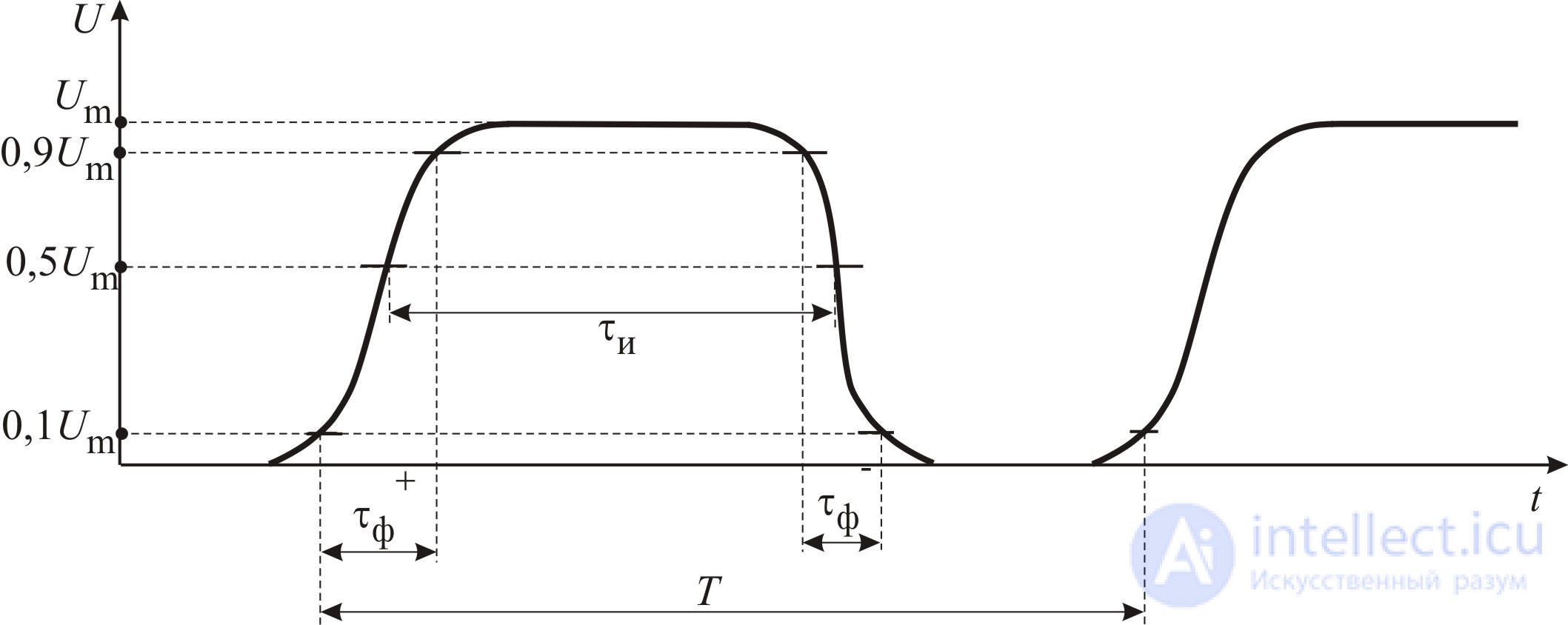
Рисунок 1.14 – Параметры периодического импульсного сигнала
Измерение периода и частоты сигнала
По определению (см. рис.1) период T – это наименьший временной интервал, через который периодический сигнал повторяет свои значения. Частота f равна количеству периодов в единицу времени. Частота связана с периодов простым обратным соотношением f = 1/Т, поэтому измерив период, легко рассчитать и обратную величину – частоту, и наоборот.
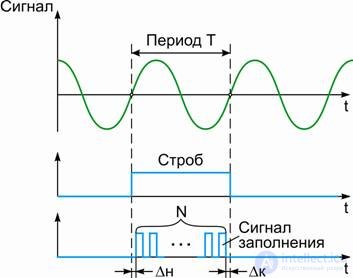
Рисунок 1 – Метод стробирования для измерения периода сигнала
Формально прописанными в ГОСТ характеристиками сигналов являются ниже следующие.
По силе сигналов практические сигналы можно разделить на две категории: энергетические сигналы и мощные сигналы. [14]
Сигналы энергии: эти сигналы энергия равна конечное положительное значение, но их средние мощности равны 0;
Сигналы мощности: средняя мощность этих сигналов равна конечному положительному значению, но их энергия бесконечна .
t}
Детерминированные сигналы - это те, значения которых в любой момент предсказуемы и могут быть вычислены с помощью математического уравнения.
Случайные сигналы - это сигналы, которые принимают случайные значения в любой данный момент времени и должны моделироваться стохастически . [15
Событие (получение записки, наблюдение сигнальной ракеты, прием символа по телеграфу) является сигналом только в той системе отношений, в которой сообщение опознается значимым (например, в условиях боевых действий сигнальная ракета — событие, значимое только для того наблюдателя, которому оно адресовано). Очевидно, что сигнал, заданный аналитически, событием не является и не несет информацию, если функция сигнала и ее параметры известны наблюдателю.
В технике сигнал всегда является событием Другими словами, событие — изменение состояния любого компонента технической системы, опознаваемое логикой системы как значимое, является сигналом. Событие, неопознаваемое данной системой логических или технических отношений как значимое, сигналом не является.
Есть два способа представления сигнала в зависимости от области определения: временной и частотный. В первом случае сигнал представляется функцией времени {\displaystyle s(t)}
характеризующей изменение его параметра.
Кроме привычного временного представления сигналов и функций при анализе и обработке данных широко используется описание сигналов функциями частоты. Действительно, любой сколь угодно сложный по своей форме сигнал можно представить в виде суммы более простых сигналов, и, в частности, в виде суммы простейших гармонических колебаний, совокупность которых называется частотным спектром сигнала.
Для перехода к частотному способу представления используется преобразование Фурье:
.
Функция 
называется спектральной функцией или спектральной плотностью. Поскольку спектральная функция является комплексной, то можно говорить о спектре амплитуд 
и спектре фаз 
.
Физический смысл спектральной функции: сигнал представляется в виде суммы бесконечного ряда гармонических составляющих (синусоид) с амплитудами 
, непрерывно заполняющими интервал частот от 
до 
, и начальными фазами 
.
Размерность спектральной функции есть размерность сигнала, умноженная на время.
В радиотехнике основным элементом кодирования является модуляция сигнала. При этом обычно рассматривается близкий к гармоническому сигнал вида s(t) = A sin(2πf·t + φ), где амплитуда A, частота f или фаза φ медленно (относительно скорости изменения синуса) изменяются в зависимости от передаваемой информации (амплитудная, частотная или фазовая модуляция, соответственно).
Стохастические модели сигнала, предполагают случайным или сам сигнал, или переносимую им информацию. Стохастическая модель сигнала часто формулируется как уравнение, связывающее сигнал с шумом, который в данном случае имитирует множество возможных информационных сообщений и называется формирующим шумом, в отличие от мешающего шума наблюдения.
Обобщением скалярной модели сигнала являются, например, векторные модели сигналов, представляющие собой упорядоченные наборы отдельных скалярных функций, с определенной взаимосвязью компонентов вектора друг с другом. На практике векторная модель соответствует, в частности, одновременному приему сигнала несколькими приемниками с последующей совместной обработкой. Еще одним расширением понятия сигнала является его обобщение на случай полей.
Сигналы в природе могут быть преобразованы в электронные сигналы с помощью различных датчиков . Примеры включают:
Другими примерами сигналов являются выход термопары , которая передает информацию о температуре, и выход pH-метра, который передает информацию о кислотности.
Исследование, описанное в статье про сигнал, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое сигнал, аналоговый сигнал, цифровой сигнал, характеристики сигнала и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории МЕТРОЛОГИЯ И ЭЛЕКТРОРАДИОИЗМЕРЕНИЯ
Комментарии
Оставить комментарий
МЕТРОЛОГИЯ И ЭЛЕКТРОРАДИОИЗМЕРЕНИЯ
Термины: МЕТРОЛОГИЯ И ЭЛЕКТРОРАДИОИЗМЕРЕНИЯ