Лекция
Привет, Вы узнаете о том , что такое погрешность измерения, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое погрешность измерения, погрешности как характеристики средств измерений , настоятельно рекомендую прочитать все из категории МЕТРОЛОГИЯ И ЭЛЕКТРОРАДИОИЗМЕРЕНИЯ.
Измерение можно считать законченным, если найден не только результат измерения, но и проведена оценка его погрешности. В метрологии определение «погрешность» является одним из центральных, причем в нем отражены понятия «погрешность результата измерения» и «погрешность средства измерения». Эти два понятия близки друг к другу и обычно их классифицируют по одинаковым признакам.
погрешность измерения — отклонение измеренного значения величины от ее истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного. Это отклонение принято называть ошибкой измерения. (В ряде источников, например в Большой советской энциклопедии, термины ошибка измерения и погрешность измерения используются как синонимы, но согласно рекомендации РМГ 29-99 термин ошибка измерения не рекомендуется применять как менее удачный, а РМГ 29-2013 его вообще не упоминает ). Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. На практике вместо истинного значения используют действительное значение величины хд, то есть значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него . Такое значение, обычно, вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому при записи результатов измерений необходимо указывать, какова их точность. Например, запись T = 2,8 ± 0,1 с; P=0,95 означает, что истинное значение величины T лежит в интервале от 2,7 с до 2,9 с с доверительной вероятностью 95%.
В конце XX века в международную метрологию была введена концепция неопределенности результата измерения, в которой не рассматриваются истинное, действительное значения измеряемой величины и погрешность измерения. Вместо этого количественно оценивается «сомнение в измеряемой величине». Неопределенность, так же как и погрешность, указывается вместе с результатом измерения. Наиболее полная запись может выглядеть следующим образом: «100,02147±0,00079 г., где число, стоящее после знака "±", — расширенная неопределенность U = kuc, полученная для uc = 35 мг и k = 2,26, соответствующего уровню доверия 95% для t-распределения c 9 степенями свободы».
Погрешностью результата измерения называют отклонение найденного значения от истинного значения измеряемой величины. Так как истинное значение измеряемой величины неизвестно, то при количественной оценке погрешности пользуются действительным значением физической величины. Это значение находится экспериментально и настолько близко к истинному значению, что для поставленной измерительной задачи может быть использовано вместо него.
Погрешность средства измерения представляет собой разность между показаниями средства измерения и истинным (действительным) значением измеряемой физической величины. Она характеризует точность результатов измерений, проводимых используемым средством.
По форме количественного выражения погрешности делят на абсолютные, относительные и приведенные.
Абсолютной погрешностью Δ, выражаемой в единицах измеряемой величины, называют отклонение результата измерения А от истинного значения Х.
Δ = А - Х, (1.7)
Разновидностью абсолютной погрешности является предельная погрешность Δт - погрешность, больше которой в данном измерительном эксперименте не может быть.
Абсолютная погрешность характеризует значение и знак полученной погрешности, но не определяет качество самого измерения. Характеристикой качества измерения является точность измерения, отражающая меру близости результата измерения к истинному значению измеряемой величины. Высокой точности измерений соответствует малая погрешность. Например, измерение силы тока в 10 и 100 А может быть выполнено с идентичной абсолютной погрешностью А = ± 1 А. Однако качество первого измерения хуже второго. Поэтому для сравнения качества измерений, используют относительную погрешность.
Относительной погрешностью δ называют отношение абсолютной погрешности измерения к истинному значению измеряемой величины:
δ = Δ / Х, (1.8)
Мерой точности измерений служит показатель, обратный модулю относительной погрешности: КТ - 1/ | δ |. Относительную погрешность δ часто выражают в процентах:
δ = 100Δ / Х %
Так как обычно Δ << Х то относительная погрешность может быть определена как δ << Δ / А или δ ≈ 100Δ / А %.
Приведенной погрешностью γ, выражающей потенциальную точность измерений, называют отношение абсолютной погрешности Δ к некоторому нормирующему значению XN (например, к конечному значению шкалы):
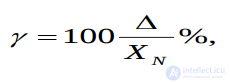
(1.9)
По характеру (закономерности) проявления погрешности делят на три основных класса: систематические, случайные и грубые (промахи).
Систематические погрешности Δс - составляющие погрешности измерений, сохраняющиеся постоянными или закономерно изменяющиеся при многократных измерениях величины в одних и тех же условиях. Об этом говорит сайт https://intellect.icu . Такие погрешности выявляют детальным анализом их возможных источников и уменьшают введением соответствующей поправки, применением более точных приборов, калибровкой приборов с помощью рабочих мер и т.п.
Случайные погрешности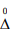 
- составляющие погрешности измерений, изменяющиеся случайным образом по значению и знаку при повторных измерениях одной и той же физической величины в одних и тех же условиях. Данные погрешности проявляются при повторных измерениях одной и той же физической величины в виде некоторого разброса получаемых результатов. Описание и оценка случайных погрешностей возможны только на основе теории вероятностей и математической статистики.
Грубые погрешности (промахи) - погрешности, существенно превышающие ожидаемые при данных условиях измерения. Они возникают из-за ошибок оператора или неучтенных внешних воздействий. В случае однократного измерения обнаружить промах нельзя. При многократных наблюдениях промахи выявляют и исключают в процессе обработки результатов наблюдений.
Итак, если не учитывать промахи, абсолютная погрешность измерения Δ определяемая выражением (2.1), представляют суммой систематической и случайной составляющих:
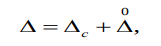(1.10)
Значит абсолютная погрешность, как и результат измерения - случайная величина.
По причинам возникновения погрешности измерения подразделяют на методические, инструментальные, внешние и субъективные (личные).
Методические погрешности возникают из-за несовершенства метода измерений, некорректности алгоритмов или формул, по которым производят вычисления результатов измерений, из-за влияния выбранного средства измерения на измеряемые параметры сигналов и т.д.
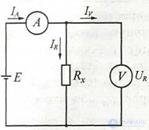
Рисунок 1.3 К примеру 2.1
Пример 2.1 Проанализируем появление методической погрешности при измерении сопротивления методом вольтметра-амперметра (рис. 2.1). Для определения значения сопротивления Rx резистора необходимо измерить ток 1R, протекающий через резистор и падение напряжения на нем UR. В приведенной схеме, реализующей этот метод, падение напряжения на резисторе измеряется вольтметром непосредственно, в то время как амперметр измеряет суммарный ток, одна часть которого протекает через резистор, другая часть через вольтметр. В результате измеренное значение сопротивления будет не RX = UR/IR а R' = URI(IR + Iy), и появится методическая погрешность ΔR = R' – RХ,. Методическая погрешность уменьшается и стремится к нулю При токе IV → 0, т.е. при внутреннем сопротивлении вольтметра RV → ∞.
Инструментальные (аппаратурные) погрешности возникают из-за несовершенства средств измерения, т.е. от их погрешностей. Уменьшают инструментальные погрешности применением более точного прибора.
Внешние погрешности связаны с отклонением одной или нескольких влияющих величин от нормальных значений или выходом их за пределы нормальной области.
Субъективные погрешности вызваны ошибками оператора при отсчете показаний (погрешности от небрежности и невнимания оператора).
По характеру поведения измеряемой величины в процессе измерений различают статические и динамические погрешности.
Статические погрешности возникают при измерении установившегося во времени значения измеряемой величины.
Динамические погрешности имеют место при динамических измерениях, когда измеряемая физическая величина изменяется во времени. Причина появления динамических погрешностей состоит в несоответствии скоростных (временных) характеристик прибора и скорости изменения измеряемой величины.
По условиям эксплуатации средства измерений различают основную и дополнительную погрешности.
Основная погрешность средств измерений имеет место при нормальных условиях эксплуатации, оговоренных в регламентирующих документах.
Дополнительная погрешность средств измерений возникает из-за выхода какой-либо из влияющих величин за пределы нормальной области значений.
При измерениях в повседневной жизни повышенная точность не всегда нужна. Однако определенная информация о возможной инструментальной составляющей погрешности измерения необходима и поэтому она должна быть каким-либо образом отражена. Такая информация содержится в указании класса точности средства измерения.
Класс точности - обобщенная характеристика средства измерения, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значения которых устанавливают в соответствующих стандартах. Можно отметить такое примечание: «Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполненных с помощью этих средств».
Классы точности присваивают средствам измерений при разработке на основании исследований и испытаний представительной партии таких устройств. Обычно их устанавливают в технических условиях на средство измерения. Пределы допускаемых погрешностей нормируют и выражают в форме абсолютной (∆си = ∆), относительной (δси = δ) или приведенной (γси = γ) погрешностей (далее индекс «си» для упрощения опущен). Форма выражения зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средства измерения.
Абсолютная погрешность средств измерений ∆СИ = ∆ состоит из аддитивной (суммируемой с измеряемой величиной) и мультипликативной(умножаемой на измеряемую величину) составляющих. Аддитивная составляющая образуется, например, из-за неточности установки на нуль перед измерением и т.д. Мультипликативные погрешности появляются вследствие изменения коэффициента усиления усилителя, коэффициента передачи цепи.
Из-за влияния многочисленных и принципиально неустранимых факторов, обусловливающих случайные погрешности, результат каждого измерения Ai будет отличаться от истинного значения X измеряемой величины: Аi - X = Δ Xi. Эту разность называют случайной погрешностью отдельного измерения.
Истинное значение X нам неизвестно. Однако, проведя большое количество измерений исследуемой величины X, можно выявить следующие статистические закономерности:
1) Если проводить серию измерений исследуемой величины и определить среднее значение, то положительные и отрицательные отклонения отдельных результатов измерений от среднего значения имеют приблизительно равную вероятность. Это является причиной того, что имеется равная вероятность (частота) отклонения результатов измерений от истинного значения величины в сторону уменьшения и увеличения, в том случае, когда систематическая погрешность равна нулю.
Среднее арифметическое значение, вычисленное на основании ряда измерений, является наиболее достоверным значением, которое можно приписать измеряемой величине. При вычислении среднего арифметического большого числа измерений погрешности отдельных измерений, имеющие разный знак, взаимно компенсируются.
2) Вероятность (частота) появления больших отклонений от полученного результата значительно меньше вероятности (частоты) появления малых отклонений. Эти статистические закономерности справедливы лишь при многократном повторении измерений.
После обработки результатов измерений, получается не абсолютно достоверный, а наиболее вероятный результат и этим результатом будет среднее арифметическое значение ряда измерений:
(1.11)
где n - число измерений.
Указанные статистические закономерности большого числа измерений позволяют поставить вопрос о законе, по которому происходит распределение случайных погрешностей. В практике электрорадиоизмерений наиболее распространенным законом распределения погрешностей является гауссовский закон распределения. Аналитически он описывается выражением:
(1.12)
где р(ΔХ) - плотность вероятности случайной погрешности ΔХ = А-X; σ - параметр, характеризующий степень случайного разброса результатов отдельных измерений относительного истинного значения X.
По своему смыслу плотность вероятности равна отношению вероятности попадания случайной величины внутрь интервала ΔХ к длине этого интервала в предположении, что последняя стремится к нулю.
Величину σ называют средним кнадратическим отклонением случайной погрешности измерения и определяют из соотношения:
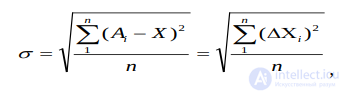
(1.13)
где Аi- численный результат отдельного измерения, n - число измерений.
Характер кривых, описываемых (1.13), показан на рис. 1.4, а для трех значений σ. Функция (1.4) графически изображается колоколообразной кривой, симметричной относительно ординат, асимптотически
Рисунок 1.4
приближающейся к оси абсцисс. Максимум этой кривой получается в точке
ΔХ = 0, а величина этого максимума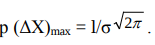 
. Как видно из рис. 1.4, чем меньше σ, тем уже кривая и, следовательно, тем реже встречаются большие отклонения, т. е. тем точнее выполняются измерения.
Как отмечалось ранее, среднее арифметическое ряда измерений А является лишь наиболее достоверным значением измеряемой величины. Представляет интерес определение погрешности вычисления среднего арифметического значения. Оценивается эта погрешность с помощью величин, аналогичных тем, при посредстве которых производится оценка погрешности отдельного измерения. Если выполнить k серий измерений, в каждом из которых производится п отдельных измерений, и вычислить среднее арифметическое значение для каждой серии, то полученные средние
арифметические значения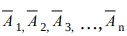 
будут несколько различаться между собой. Эти средние значения будут отличаться от истинного значения X измеряемой величины на случайные величины и, следовательно, будут распределяться около X по Гауссовскому закону (1.4). Для получения представления о случайном разбросе среднего арифметического относительно точного значения X измеряемой величины нужно вычислить среднее квадратическое отклонение от среднего арифметического. В теории погрешностей доказывается, что это отклонение в n раз меньше средней квадратической погрешности отдельного измерения, т. е.
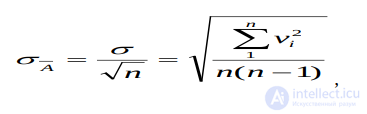, (1.14)
σA - средняя квадратическая погрешность среднего
где
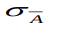арифметического из ряда измерений;
σ - средняя квадратическая погрешность отдельного измерения;
n - число измерений в серии.
Из данного выражения видно, что увеличение числа повторных измерений n приводит к уменьшению σA результата измерений. средней квадратической погрешности
На практике (особенно при малом значении n) необходимо оценить точность и надежность полученных результатов для среднего значения и среднего квадратического отклонения. Для этой цели пользуются доверительной вероятностью и доверительным интервалом. Под доверительной вероятностью понимают вероятность появления погрешности, не выходящей за некоторые принятые границы. Этот интервал называют доверительным интервалом, а характеризующую его вероятность - доверительной вероятностью.
На практике приходится оценивать погрешности по результатам сравнительно небольшого количества измерения. Применение формулы (1.14) в этом случае дает заниженное значение доверительного интервала, т. е. оценка точности измерения оказывается неоправданно завышенной. В этом случае уточнить доверительный интервал можно с помощью коэффициентов Стьюдента tn, которые зависят от задаваемой доверительной вероятности р и числа измерений n.
Для определения доверительного интервала среднюю квадратическую погрешность надо умножить на коэффициент Стьюдента. Окончательный результат можно записать так:
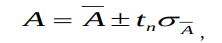(1.15)
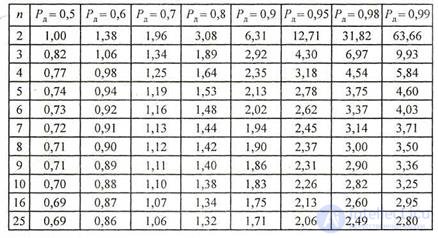
Значения коэффициентов tn, необходимых при расчетах приведены в табл. 1.1.
Общие сведения об обработке результатов измерений
Таблица 1.1 Коэффициенты Стьюдента t (Pд, n)
Информация, изложенная в данной статье про погрешность измерения , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое погрешность измерения, погрешности как характеристики средств измерений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории МЕТРОЛОГИЯ И ЭЛЕКТРОРАДИОИЗМЕРЕНИЯ
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
МЕТРОЛОГИЯ И ЭЛЕКТРОРАДИОИЗМЕРЕНИЯ
Термины: МЕТРОЛОГИЯ И ЭЛЕКТРОРАДИОИЗМЕРЕНИЯ