Лекция
Привет, Вы узнаете о том , что такое энтропия, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое энтропия, информация для систем с непрерывным множеством состояний , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.
До сих пор мы рассматривали физические системы, различные состояния которых 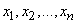 можно было все перечислить; вероятности этих состояний были какие-то отличные от нуля величины
можно было все перечислить; вероятности этих состояний были какие-то отличные от нуля величины 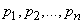 . Такие системы аналогичны прерывным (дискретным) случайным величинам, принимающим значения
. Такие системы аналогичны прерывным (дискретным) случайным величинам, принимающим значения 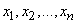 с вероятностями
с вероятностями 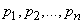 . На практике часто встречаются физические системы другого типа, аналогичные непрерывным случайным величинам. Состояния таких систем нельзя перенумеровать: они непрерывно переходят одно в другое, причем каждое отдельное состояние имеет вероятность, равную нулю, а распределение вероятностей характеризуется некоторой плотностью. Такие системы, по аналогии с непрерывными случайными величинами, мы будем называть «непрерывными», в отличие от ранее рассмотренных, которые мы будем называть «дискретными». Наиболее простой пример непрерывной системы - это система, состояние которой описывается одной непрерывной случайной величиной
. На практике часто встречаются физические системы другого типа, аналогичные непрерывным случайным величинам. Состояния таких систем нельзя перенумеровать: они непрерывно переходят одно в другое, причем каждое отдельное состояние имеет вероятность, равную нулю, а распределение вероятностей характеризуется некоторой плотностью. Такие системы, по аналогии с непрерывными случайными величинами, мы будем называть «непрерывными», в отличие от ранее рассмотренных, которые мы будем называть «дискретными». Наиболее простой пример непрерывной системы - это система, состояние которой описывается одной непрерывной случайной величиной  с плотностью распределения
с плотностью распределения 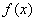 . В более сложных случаях состояние системы описывается несколькими случайными величинами
. В более сложных случаях состояние системы описывается несколькими случайными величинами 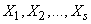 с плотностью распределения
с плотностью распределения 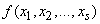 . Тогда ее можно рассматривать как объединение
. Тогда ее можно рассматривать как объединение 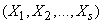 простых систем
простых систем 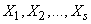 .
.
Рассмотрим простую систему  , определяемую одной непрерывной случайной величиной
, определяемую одной непрерывной случайной величиной  с плотностью распределения
с плотностью распределения 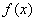 (рис. 18.7.1). Попытаемся распространить на эту систему введенное в
(рис. 18.7.1). Попытаемся распространить на эту систему введенное в 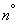 18.1 понятие энтропии.
18.1 понятие энтропии.
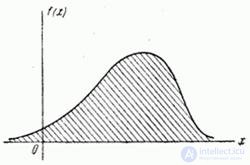
Рис. 18.7.1.
Прежде всего отметим, что понятие «непрерывной системы», как и понятие «непрерывной случайной величины», является некоторой идеализацией. Например, когда мы считаем величину  - рост наугад взятого человека - непрерывной случайной величиной, мы отвлекаемся от того, что фактически никто не измеряет рост точнее, чем до 1 см, и что различить между собой два значения роста, разнящиеся, скажем, на 1 мм, практически невозможно. Тем не менее, данную случайную величину естественно описывать как непрерывную, хотя можно было бы описать ее и как дискретную, считая совпадающими те значения роста, которые различаются менее чем на 1 см.
- рост наугад взятого человека - непрерывной случайной величиной, мы отвлекаемся от того, что фактически никто не измеряет рост точнее, чем до 1 см, и что различить между собой два значения роста, разнящиеся, скажем, на 1 мм, практически невозможно. Тем не менее, данную случайную величину естественно описывать как непрерывную, хотя можно было бы описать ее и как дискретную, считая совпадающими те значения роста, которые различаются менее чем на 1 см.
Точно таким образом, установив предел точности измерений, т. е. некоторый отрезок 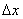 , в пределах которого состояния системы
, в пределах которого состояния системы  практически неразличимы, можно приближенно свести непрерывную систему
практически неразличимы, можно приближенно свести непрерывную систему  к дискретной. Это равносильно замене плавной кривой
к дискретной. Это равносильно замене плавной кривой 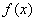 ступенчатой, типа гистограммы (рис. 18.7.2); при этом каждый участок (разряд) длины
ступенчатой, типа гистограммы (рис. 18.7.2); при этом каждый участок (разряд) длины 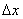 заменяется одной точкой-представителем.
заменяется одной точкой-представителем.
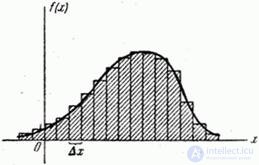
Рис. 18.7.2.
Площади прямоугольников изображают вероятности попадания в соответствующие разряды: 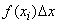 . Если условиться считать неразличимыми состояния системы, относящиеся к одному разряду, и объединить их все в одно состояние, то можно приближенно определить энтропию системы
. Если условиться считать неразличимыми состояния системы, относящиеся к одному разряду, и объединить их все в одно состояние, то можно приближенно определить энтропию системы  , рассматриваемой с точностью до
, рассматриваемой с точностью до 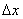 :
:
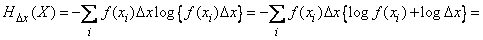
 . (18.7.1)
. (18.7.1)
При достаточно малом 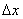 :
:
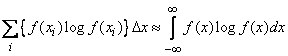 ,
,
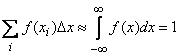
и формула (18.7.1) принимает вид:
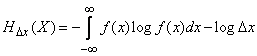 . (18.7.2)
. (18.7.2)
Заметим, что в выражении (18.7.2) первый член получился совсем не зависящим от 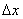 - степени точности определения состояний системы. Зависит от
- степени точности определения состояний системы. Зависит от 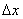 только второй член
только второй член 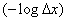 , который стремится к бесконечности при
, который стремится к бесконечности при 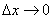 . Это и естественно, так как чем точнее мы хотим задать состояние системы
. Это и естественно, так как чем точнее мы хотим задать состояние системы  , тем большую степень неопределенности мы должны устранить, и при неограниченном уменьшении
, тем большую степень неопределенности мы должны устранить, и при неограниченном уменьшении 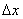 эта неопределенность растет тоже неограниченно.
эта неопределенность растет тоже неограниченно.
Итак, задаваясь произвольно малым «участком нечувствительности» 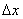 наших измерительных приборов, с помощью которых определяется состояние физической системы
наших измерительных приборов, с помощью которых определяется состояние физической системы  , можно найти энтропию
, можно найти энтропию 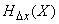 по формуле (18.7.2), в которой второй член неограниченно растет с уменьшением
по формуле (18.7.2), в которой второй член неограниченно растет с уменьшением 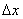 . Сама
энтропия
. Сама
энтропия 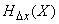 отличается от этого неограниченно растущего члена на независимую от
отличается от этого неограниченно растущего члена на независимую от 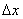 величину
величину
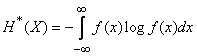 . (18.7.3)
. (18.7.3)
Эту величину можно назвать «приведенной энтропией» непрерывной системы  . Энтропия
. Энтропия 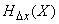 выражается через приведенную энтропию
выражается через приведенную энтропию 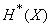 формулой
формулой
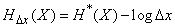 . (18.7.4)
. (18.7.4)
Соотношение (18.7.4) можно истолковать следующим образом: от точности измерения 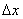 зависит только начало отсчета, при котором вычисляется энтропия.
зависит только начало отсчета, при котором вычисляется энтропия.
В дальнейшем для упрощения записи мы будем опускать индекс 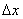 в обозначении энтропии и писать просто
в обозначении энтропии и писать просто 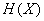 ; наличие
; наличие 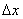 в правой части всегда укажет, о какой точности идет речь.
в правой части всегда укажет, о какой точности идет речь.
Формуле (18.7.2) для энтропии можно придать более компактный вид, если, как мы это делали для прерывных величин, записать ее в виде математического ожидания функции. Прежде всего перепишем (18.7.2) в виде
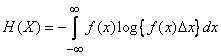 . (18.7.5)
. (18.7.5)
Это есть не что иное, как математическое ожидание функции 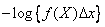 от случайной величины
от случайной величины  с плотностью
с плотностью 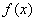 :
:
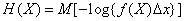 . (18.7.6)
. (18.7.6)
Аналогичную форму можно придать величине 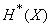 :
:
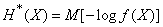 . (18.7.7)
. (18.7.7)
Перейдем к определению условной энтропии. Об этом говорит сайт https://intellect.icu . Пусть имеются две непрерывные системы:  и
и 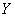 . В общем случае эти системы зависимы. Обозначим
. В общем случае эти системы зависимы. Обозначим 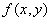 плотность распределения для состояний объединенной системы
плотность распределения для состояний объединенной системы 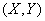 ;
; 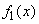 - плотность распределения системы
- плотность распределения системы  ;
; 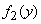 - плотность распределения системы
- плотность распределения системы 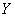 ;
; 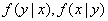 - условные плотности распределения.
- условные плотности распределения.
Прежде всего определим частную условную энтропию 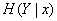 , т. е. энтропию системы
, т. е. энтропию системы 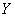 при условии, что система
при условии, что система  приняла определенное состояние
приняла определенное состояние 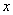 . Формула для нее будет аналогична (18.4.2), только вместо условных вероятностей
. Формула для нее будет аналогична (18.4.2), только вместо условных вероятностей 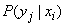 будут стоять условные законы распределения
будут стоять условные законы распределения 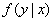 и появится слагаемое
и появится слагаемое 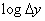 :
:
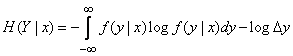 . (18.7.8)
. (18.7.8)
Перейдем теперь к полной (средней) условной энтропии 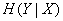 , для этого нужно осреднить частную условную энтропию
, для этого нужно осреднить частную условную энтропию 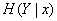 по всем состояниям
по всем состояниям 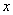 с учетом их вероятностей, характеризуемых плотностью
с учетом их вероятностей, характеризуемых плотностью 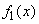 :
:
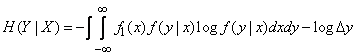 (18.7.9)
(18.7.9)
или, учитывая, что
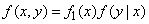 ,
,
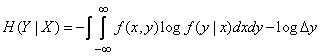 . (18.7.10)
. (18.7.10)
Иначе эта формула может быть записана в виде
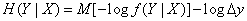 (18.7.11)
(18.7.11)
или
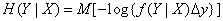 . (18.7.12)
. (18.7.12)
Определив таким образом условную энтропию, покажем, как она применяется при определении энтропии объединенной системы.
Найдем сначала энтропию объединенной системы непосредственно. Если «участками нечувствительности» для систем  и
и 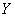 будут
будут 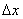 и
и 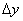 , то для объединенной системы
, то для объединенной системы 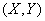 роль их будет играть элементарный прямоугольник
роль их будет играть элементарный прямоугольник 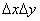 . Энтропия системы
. Энтропия системы 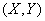 будет
будет
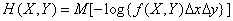 . (18.7.13)
. (18.7.13)
Так как
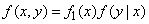 ,
,
то и
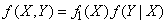 . (18.7.14)
. (18.7.14)
Подставим (18.7.14) в (18.7.13):
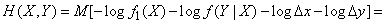
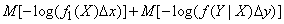 ,
,
или, по формулам (18.7.6) и (18.7.12)
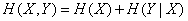 , (18.7.15)
, (18.7.15)
т. е. теорема об энтропии сложной системы остается в силе и для непрерывных систем.
Если  и
и 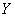 независимы, то энтропия объединенной системы равна сумме энтропий составных частей:
независимы, то энтропия объединенной системы равна сумме энтропий составных частей:
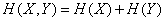 . (18.7.16)
. (18.7.16)
Пример 1. Найти энтропию непрерывной системы  , все состояния которой на каком-то участке
, все состояния которой на каком-то участке 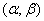 одинаково вероятны:
одинаково вероятны:
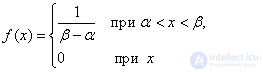
Решение.
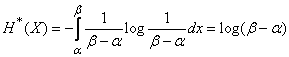 ;
;
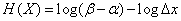
или
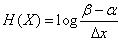 . (18.7.17)
. (18.7.17)
Пример 2. Найти энтропию системы  , состояния которой распределены по нормальному закону:
, состояния которой распределены по нормальному закону:
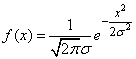 .
.
Решение.
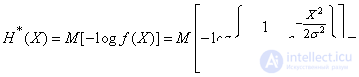
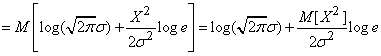 .
.
Но
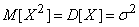 ,
,
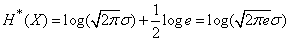
и
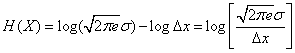 . (18.7.18)
. (18.7.18)
Пример 3. Состояние самолета характеризуется тремя случайными величинами: высотой 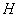 , модулем скорости
, модулем скорости 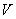 и углом
и углом 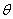 , определяющим направление полета. Высота самолета распределена с равномерной плотностью на участке
, определяющим направление полета. Высота самолета распределена с равномерной плотностью на участке 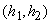 ; скорость
; скорость 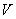 - по нормальному закону с м.о.
- по нормальному закону с м.о. 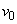 и с.к.о.
и с.к.о. 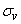 ; угол
; угол 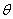 - с равномерной плотностью на участке
- с равномерной плотностью на участке 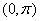 . Величины
. Величины 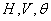 независимы. Найти энтропию объединенной системы.
независимы. Найти энтропию объединенной системы.
Решение.
Из примера 1 (формула (18.7.17)) имеем
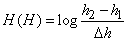 ,
,
где 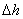 - «участок нечувствительности» при определении высоты.
- «участок нечувствительности» при определении высоты.
Так как энтропия случайной величины не зависит от ее математического ожидания, то для определения энтропии величины 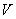 воспользуемся формулой (18.7.18):
воспользуемся формулой (18.7.18):
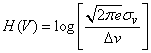 .
.
Энтропия величины 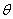 :
:
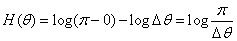 .
.
Окончательно имеем:
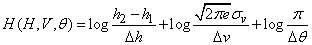
или
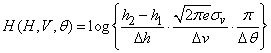 . (18.7.19)
. (18.7.19)
Заметим, что каждый из сомножителей под знаком фигурной скобки имеет один и тот же смысл: он показывает, сколько «участков нечувствительности» укладывается в некотором характерном для данной случайной величины отрезке. В случае распределения с равномерной плотностью этот участок представляет собой просто участок возможных значений случайной величины; в случае нормального распределения этот участок равен 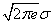 , где
, где 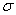 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Таким образом, мы распространили понятие энтропии на случай непрерывных систем. Аналогично может быть распространено и понятие информации. При этом неопределенность, связанная с наличием в выражении энтропии неограниченно возрастающего слагаемого, отпадает: при вычислении информации, как разности двух энтропий, эти члены взаимно уничтожаются. Поэтому все виды информации, связанные с непрерывными величинами, оказываются не зависящими от «участка нечувствительности» 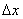 .
.
Выражение для полной взаимной информации, содержащейся в двух непрерывных системах  и
и 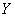 , будет аналогично выражению (18.5.4), но с заменой вероятностей законами распределения, а сумм - интегралами:
, будет аналогично выражению (18.5.4), но с заменой вероятностей законами распределения, а сумм - интегралами:
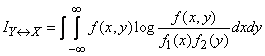 (18.7.20)
(18.7.20)
или, применяя знак математического ожидания,
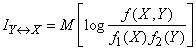 . (18.7.21)
. (18.7.21)
Полная взаимная информация 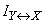 как и в случае дискретных систем, есть неотрицательная величина, обращающаяся в нуль только тогда, когда системы
как и в случае дискретных систем, есть неотрицательная величина, обращающаяся в нуль только тогда, когда системы  и
и 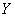 независимы.
независимы.
Пример 4. На отрезке 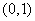 выбираются случайным образом, независимо друг от друга, две точки
выбираются случайным образом, независимо друг от друга, две точки 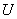 и
и 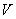 , каждая из них распределена на этом отрезке с равномерной плотностью. В результате опыта одна из точек легла правее, другая - левее. Сколько информации о положении правой точки дает значение положения левой?
, каждая из них распределена на этом отрезке с равномерной плотностью. В результате опыта одна из точек легла правее, другая - левее. Сколько информации о положении правой точки дает значение положения левой?
Решение. Рассмотрим две случайные точки 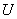 и
и 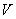 на оси абсцисс
на оси абсцисс 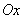 (рис. 18.7.3).
(рис. 18.7.3).
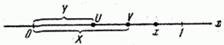
Рис. 18.7.3.
Обозначим 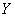 абсциссу той из них, которая оказалась слева, а
абсциссу той из них, которая оказалась слева, а  - абсциссу той, которая оказалась справа (на рис. 18.7.3 слева оказалась точка
- абсциссу той, которая оказалась справа (на рис. 18.7.3 слева оказалась точка 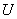 , но могло быть и наоборот). Величины
, но могло быть и наоборот). Величины  и
и 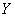 определяются через
определяются через 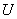 и
и 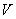 следующим образом
следующим образом
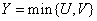 ;
; 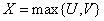 .
.
Найдем закон распределения системы 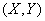 . Так как
. Так как 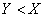 , то он будет существовать только в области
, то он будет существовать только в области 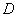 , заштрихованной на рис. 18.7.4.
, заштрихованной на рис. 18.7.4.
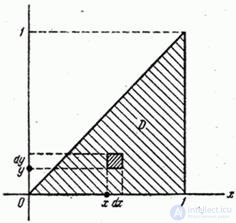
Рис. 18.7.4.
Обозначим 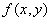 плотность распределения системы
плотность распределения системы 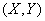 и найдем элемент вероятности
и найдем элемент вероятности 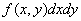 , т. е. вероятность того, что случайная точка
, т. е. вероятность того, что случайная точка 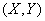 попадет в элементарный прямоугольник
попадет в элементарный прямоугольник 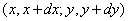 . Это событие может произойти двумя способами: либо слева окажется точка
. Это событие может произойти двумя способами: либо слева окажется точка 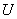 , а справа
, а справа 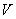 , либо наоборот. Следовательно,
, либо наоборот. Следовательно,
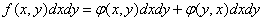 ,
,
где 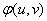 обозначена плотность распределения системы величин
обозначена плотность распределения системы величин 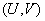 .
.
В данном случае
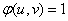
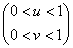 ,
,
следовательно,
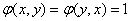 ;
;
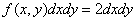
и

Найдем теперь законы распределения отдельных величин, входящих в систему:
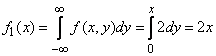 при
при 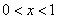 ;
;
аналогично
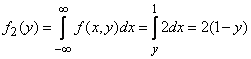 при
при 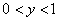 .
.
Графики плотностей 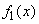 и
и 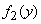 изображены на рис. 18.7.5.
изображены на рис. 18.7.5.
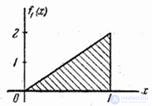
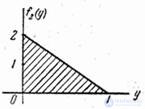
Рис 18.7.5.
Подставляя 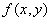 ,
, 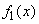 и
и 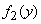 в формулу (18.7.20), получим
в формулу (18.7.20), получим
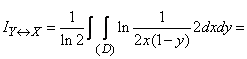
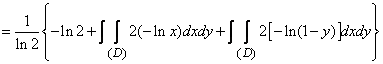 .
.
В силу симметрии задачи последние два интеграла равны, и
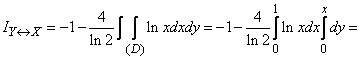
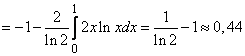 (дв. ед.).
(дв. ед.).
Пример 5. Имеется случайная величина  , распределенная по нормальному закону с параметрами
, распределенная по нормальному закону с параметрами 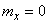 ,
, 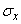 . Величина
. Величина  измеряется с ошибкой
измеряется с ошибкой 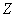 , тоже распределенной по нормальному закону с параметрами
, тоже распределенной по нормальному закону с параметрами 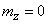 ,
, 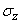 . Ошибка
. Ошибка 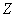 не зависит от
не зависит от  . В нашем распоряжении - результат измерения, т. е. случайная величина
. В нашем распоряжении - результат измерения, т. е. случайная величина
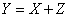
Определить, сколько информации о величине  содержит величина
содержит величина 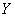 .
.
Решение. Воспользуемся для вычисления информации формулой (18.7.21), т. е. найдем ее как математическое ожидание случайной величины
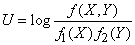 . (18.7.22)
. (18.7.22)
Для этого сначала преобразуем выражение
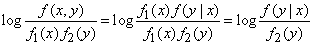 .
.
В нашем случае
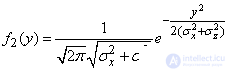 ,
,
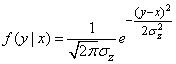 (см. главу 9).
(см. главу 9).
Выражение (18.7.22) равно:
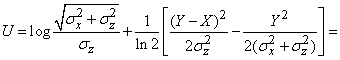
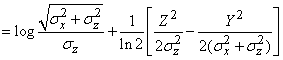 .
.
Отсюда
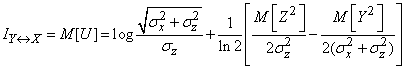 . (18.7.23)
. (18.7.23)
Ho 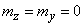 , следовательно,
, следовательно,
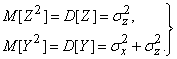 (18.7.24)
(18.7.24)
Подставляя (18.7.24) в (18.7.23), получим
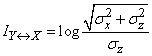 (дв. ед.).
(дв. ед.).
Например, при 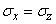
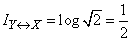 (дв. ед.).
(дв. ед.).
Если 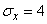 ;
; 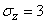 , то
, то 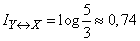 (дв. ед.).
(дв. ед.).
Информация, изложенная в данной статье про энтропия , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое энтропия, информация для систем с непрерывным множеством состояний и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования
Комментарии
Оставить комментарий
Теория информации и кодирования
Термины: Теория информации и кодирования