18.4. Условная энтропия. Объединение зависимых систем кратко

Привет, Вы узнаете о том , что такое условная энтропия объединение зависимых систем, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое условная энтропия объединение зависимых систем , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

Пусть имеются две системы 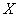 и 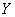, в общем случае зависимые. Предположим, что система  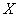приняла состояние 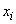. Обозначим  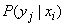условную вероятность того, что система  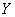примет состояние  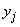при условии, что система  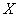находится в состоянии :

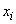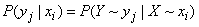.                    (18.4.1)

 

Определим теперь условную энтропию системы 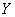 при условии, что система  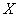находится в состоянии 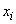. Обозначим ее 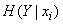. По общему определению, имеем:

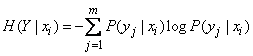                   (18.4.2)

или

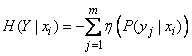.                      (18.4.2')

Формулу (18.4.2) можно также записать в форме математического ожидания:

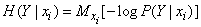,                   (18.4.3)

где знаком 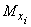 обозначено условное математическое ожидание величины, стоящей в скобках, при условии .

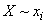Условная энтропия зависит от того, какое состояние 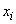 приняла система 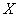; для одних состояний она будет больше, для других - меньше. Определим среднюю, или полную, энтропию системы  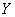с учетом того, что система может принимать разные состояния. Для этого нужно каждую условную энтропию (18.4.2) умножить на вероятность соответствующего состояния  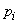и все такие произведения сложить. Обозначим полную условную энтропию :

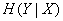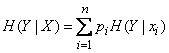                 (18.4.4)

или, пользуясь формулой (18.4.2),

.

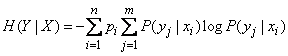Внося 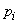 под знак второй суммы, получим:

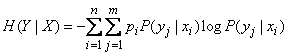           (18.4.5)

или

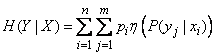.                (18.4.5')

Но по теореме умножения вероятностей 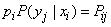, следовательно,

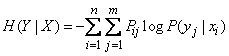.            (18.4.6)

Выражению (18.4.6) тоже можно придать форму математического ожидания:

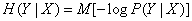.                                  (18.4.7)

Величина 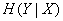 характеризует степень неопределенности системы 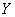, остающуюся после того, как состояние системы  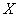полностью определилось. Будем называть ее полной условной энтропией системы  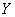относительно .

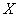Пример 1. Имеются две системы 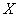 и 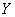, объединяемые в одну 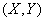; вероятности состояний системы  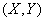заданы таблицей

	0,1	0,2	0	0,3
	0	0,3	0	0,3
	0	0,2	0,2	0,4
	0,1	0,7	0,2

Определить полные условные энтропи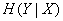и  и .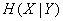

Решение. Об этом говорит сайт https://intellect.icu . Складывая вероятности 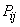 по столбцам, получим вероятности :

; ; .

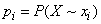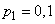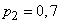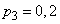Записываем их в нижней, добавочной строке таблицы. Аналогично, складывая 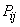 по строкам, найдем:

; ;    

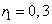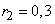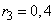
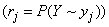
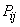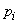и запишем справа дополнительным столбцом. Деля  на , получим таблицу условных вероятностей :

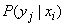По формуле (18.4.5') находим 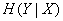. Так как условные энтропии пр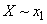и  и 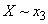 равны нулю, то

.

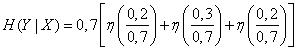Пользуясь таблицей 7 приложения, находим

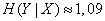 (дв. ед.).

Аналогично определим 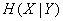. Из формулы (18.4.5'), меняя местам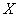и  и 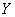, получим:

.

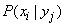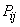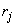Составим таблицу условных вероятностей . Деля  на  получим:

Отсюда

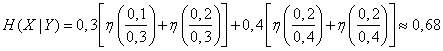 (дв. сл.).

Пользуясь понятием условной энтропии, можно определить энтропию объединенной системы через энтропию ее составных частей.

Докажем следующую теорему:

Если две системы 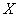 и 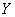 объединяется в одну, то энтропия объединенной системы равна энтропии одной из ее составных частей плюс условная энтропия второй части относительно первой:

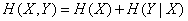.                       (18.4.8)

Для доказательства запишем 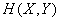 в форме математического ожидания (18.3.3):

.

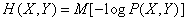По теореме умножения вероятностей

,

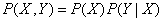следовательно,

,

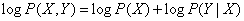откуда

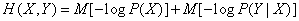
или, по формулам (18.2.11), (18.3.3)

,

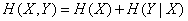что и требовалось доказать.

В частном случае, когда системы 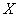 и 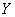 независимы, 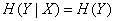, и мы получаем уже доказанную в предыдущем  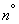теорему сложения энтропий:

.

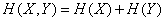В общем случае

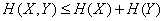.                 (18.4.9)

Соотношение (18.4.9) следует из того, что полная условная энтропия 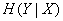 не может превосходить безусловной:

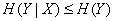.                             (18.4.10)

Неравенство (18.4.10) будет доказано в 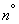 18.6. Интуитивно оно представляется довольно очевидным: ясно, что степень неопределенности системы не может увеличиться оттого, что состояние какой-то другой системы стало известным.

Из соотношения (18.4.9) следует, что энтропия сложной системы достигает максимума в крайнем случае, когда ее составные части независимы.

Рассмотрим другой крайний случай, когда состояние одной из систем (например 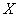) полностью определяет собой состояние другой (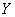). В этом случае  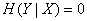и формула (18.4.7) дает

.

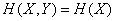Если состояние каждой из систем 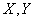 однозначно определяет состояние другой (или, как говорят, системы  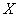и 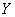 эквивалентны), то

.

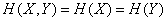Теорему об энтропии сложной системы легко можно распространить на любое число объединяемых систем:

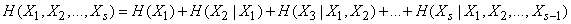,         (18.4.11)

где энтропия каждой последующей системы вычисляется при условии, что состояние всех предыдущих известно.

 

Информация, изложенная в данной статье про условная энтропия объединение зависимых систем , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое условная энтропия объединение зависимых систем и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования

Из статьи мы узнали кратко, но содержательно про условная энтропия объединение зависимых систем