7.1 Линейные коды. Общие методы построения

Привет, сегодня поговорим про линейные коды общие методы построения, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое линейные коды общие методы построения , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

Тема 5. Регулярные методы построения двоичных помехоустойчивых кодов.

Лекция 7.

7.1 Линейные коды. Общие методы построения.

 

Рассмотрим класс помехоустойчивых алгебраических кодов, называемых линейными или часто линейными групповыми.

Определение: Линейными называют блоковые коды, дополнительные разряды которых образуются путем линейных операций над информационными разрядами.

Здесь используется понятие линейная операция. В теории кодирования в качестве линейной операции сложения используется сложение по модулю 2 (+).

 

7.2 Определение числа добавочных разрядов r.

Для определения числа добавочных разрядов можно воспользоваться уже нам известной формулой границы Хэмминга:

 

_{<![if !vml]>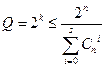<![endif]>}

 

Если s=l, то есть строится код, исправляющий максимум однократные ошибки, то :

_{<![if !vml]><![endif]>},

откуда получаем

 

2^r≥r+k

 

С учетом последней формулы ищется наименьшее r при котором удовлетворяется это неравенство.

Пример: n=7, тогда путем простого перебора легко найти, что r=3. И соответствующий код имеет вид n(7,4).

 

7.3 Построение образующей(порождающей) матрицы |OM|.

 

Линейные коды обладают следующим свойством:

- из всего множества 2^k разрешенных кодовых слов, образующих линейную группу, можно выделить подмножества из k слов, обладающих свойством линейной независимости.

Линейная независимость означает, что никакое из слов, входящих в подмножество линейно-независимых кодовых слов, нельзя получить путем суммирования (с помощью линейного выражения) любых других слов, входящих в это подмножество.

В то же время любое из разрешенных кодовых слов можно получить путем суммирования определенных линейно-независимых слов.

Таким образом, построение кодовых комбинаций линейного кода связано с линейными операциями. Для выполнения таких операций удобно пользоваться хорошо разработанным аппаратом матричных вычислений.

Для образования n -разрядных кодовых слов из k- разрядных кодируемых слов (кодирования) используют матрицу, которая называется образующей(порождающей).

Образующая матрица получается путем записи в столбец k линейно-независимых слов.

Обозначим кодируемую информационную последовательность X и будем записывать ее в виде матрицы-строки ||X|| размерностью 1*k, например:

||X||=||11001||, где k=5.

 

Один из способов построения образующей (порождающей) матрицы следующий: Она строится из единичной матрицы ||I||размерностью k*k и приписанной к ней справа матрицы добавочных (избыточных) разрядов ||МДР|| размерности k*r.

 

<![if !vml]>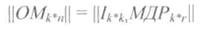<![endif]>

 

где при k=4

 

<![if !vml]><![endif]>

 

Такая структура ОМ обеспечивает получение систематического кода.

Порядок построения матрицы МДР будет рассмотрен ниже.

 

7.4 Порядок кодирования.

 

Кодовое слово КС получается путем умножения матрицы информационной последовательности ||Х|| на образующую матрицу ||ОМ||:

<![if !vml]>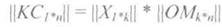<![endif]>

Умножение выполняется по правилам матричного умножения: (ТАК натек)

 

<![if !vml]>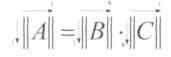<![endif]>

 

Надо только помнить, что сложение здесь ведется по модулю 2.

Пример:

допустим, образующая матрица

 

1000 110

0100 111

||ОМ||= 0010 011

0001 101

 

и вектор-строка информационной последовательности

 

<![if !vml]>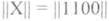<![endif]>.

Так как множимая матрица имеет всего одну строку, умножение упрощается. Об этом говорит сайт https://intellect.icu . В этом случае следует поставить в соответствие строкам образующей(порождающей) матрицы ||ОМ|| разряды матрицы информационной последовательности ||X|| и сложить те строки образующей(порождающей) матрицы, которые соответствуют единичным разрядам матрицы ||Х||.

 

<![if !vml]><![endif]>

 

Заметим, что ||KC|| = ||X, ДР||,

где ||X||- информационная последовательность (т.к. умножается на единичную матрицу ||I||),

а ||ДР|| - добавочные разряды, зависящие от матрицы добавочных разрядов ||МДР||:

|| ДР ||= || Х || * || МДР||

 

7.5 Порядок декодирования.

В результате передачи кодового слова через канал оно может быть искажено помехой. Это приведет к тому, что принятое кодовое слово ||ПКС|| может не совпасть с исходным ||КС||.

Искажение можно описать с помощью следующей формулы:

|| ПКС || = ||КС || + ||ВО ||,

 

где ||ВО|| - вектор ошибки - матрица-строка размерностью 1*n, с 1 в тех позициях, в которых произошли искажения.

Декодирование основано на нахождении так называемого опознавателя или синдрома ошибки -матрицы-строки ||ОП|| длиной r разрядов (r- количество добавочных или избыточных разрядов в кодовом слове).

Опознаватель используется для нахождения предполагаемого вектора ошибки.

Опознаватель находят по следующей формуле:

 

||ОП|| = ||ПКС||* ||ТПМ||,

 

где ||ПКС||- принятое и, возможно, искаженное кодовое слово;

||ТПМ||,- транспонированная проверочная матрица, которая получается из матрицы добавочных разрядов ||МДР|| путем приписывания к ней снизу единичной матрицы:

 

<![if !vml]><![endif]>

 

Пример ||ТПМ||:

 

<![if !vml]><![endif]>

 

Поскольку ||ПКС|| = ||КС|| + ||BO||, последнюю формулу можно записать в виде:

 

||ОП|| = ||КС|| * ||ТПМ||+||ВО|| * ||ТПМ||.

 

Рассмотрим первое слагаемое.

 

||КC|| - матрица-строка, причем первые k разрядов - информационные.

Докажем теперь, что произведение кодового слова ||КС|| на ||ТПМ|| приводит к получению нулевой матрицы ||0||.

Поскольку ||КС|| - матрица-строка, возможен упрощенный порядок умножения матриц, рассмотренных выше.

 

<![if !vml]>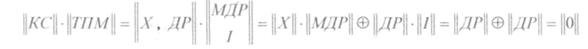<![endif]>

 

Следовательно, первое слагаемое в

 

||ОП|| = ||КС|| * ||ТПМ|| + ||ВО|| * ||ТПМ||

 

всегда равно нулю и опознаватель полностью зависит от вектора ошибки ||ВО||.

Если теперь подобрать такую проверочную матрицу ТПМ, а значит и МДР, чтобы разным векторам ошибки соответствовали разные опознаватели ОП, то по этим опознавателям можно будет находить вектор ошибки ВО, а значит и исправлять эти ошибки.

Соответствие опознавателей векторам ошибки находится заранее путем перемножения векторов исправляемых ошибок на ТПМ;

 

<![if !vml]>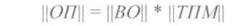<![endif]>

 

Таким образом, способность кода исправлять ошибки целиком определяется ||МДР||. Для построения МДР для кодов, исправляющих однократные ошибки нужно в каждой строке МДР иметь не менее 2-х единиц. При этом также необходимо иметь хотя бы одно различие между двумя любыми строчками МДР.

Полученный нами код неудобен тем, что опознаватель, хотя и связан однозначно с номером искаженного разряда, как число не равен ему. Для поиска искаженного разряда нужно использовать дополнительную таблицу соответствия между опознавателем и этим номером. Коды, в которых опознаватель как число определяет позицию искаженного разряда, были найдены и получили название кодов Хэмминга.

Построение МДР для случая исправления многократных ошибок значительно усложняется. Разными авторами были найдены различные алгоритмы построения ||МДР || для этого случая, а соответствующие коды называются именами их авторов.

 

7.6 Систематические коды. Код Хэмминга.

 

Систематические коды представляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях .

Систематические коды являются равномерными, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Систематические коды могут строиться, как линейные на основе производящей матрицы, как это уже было рассмотрено.

Обычно производящая матрица строится при помощи двух матриц:

Единичной, ранг которой определяется числом информационных разрядов, и добавочной, число столбцов которой определяется числом контрольных разрядов кода. Каждая строка добавочной матрицы должна содержать не менее d₀ -1 единиц, а сумма по модулю для любых строк не менее d₀-2 единиц (где d₀-минимальное кодовое расстояние).

Производящая матрица позволяет находить все остальные кодовые комбинации.

Код Хэмминга является типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Он настолько хорошо изучен, что уже выработался четкий алгоритм его построения :

Код Хэмминга представляет собой один из важнейших классов линейных кодов, нашедших широкое применение на практике и имеющих простой и удобный для технической реализации алгоритм обнаружения и исправления ошибок.

Соотношения между n, r, k для кода Хэмминга представлены в таблице. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие - контрольными. Практика показала, что номера контрольных символов удобно выбирать по закону

2ⁱ, где i = 0, 1, 2, 3, ... - натуральный ряд чисел.

Номера контрольных символов в этом случае равны 1, 2, 4, 16, 32... Затем определяют значения контрольных коэффициентов (0 или 1), руководствуясь следующим правилом:

сумма единиц на проверочных позициях должна быть четной. Если эта сумма четна -значение контрольного коэффициента нуль, в противном случае - единица.

 

Соотношения между количеством информационных и контрольных символов в коде Хэмминга

Табл.7.1

<![if !vml]>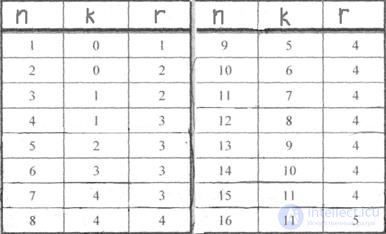<![endif]>

Проверочные позиции выбирают следующим образом. Составляют табличку для ряда натуральных чисел в двоичном коде. Число ее строк n=r+k. Первой строке соответствует проверочный коэффициент a₁, второй а₂ и т. д.:

 

<![if !vml]><![endif]>

 

Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу:

в первую проверку входят коэффициенты, которые содержат единицу в младшем разряде (a₁, а₃, a₅, a₇, a₉, a₁₁ и т. д.);

во вторую - во втором разряде (а₂, а₃, а₅, а₇, а₉, a₁₁ и т. д.);

в третью - в третьем разряде и т. д.

Номера проверочных коэффициентов соответствуют номерам проверочных позиций, что позволяет составить общую таблицу проверок.

Номера проверочных позиций кода Хэмминга

Табл.7.2

<![if !vml]><![endif]>

 

Построение кода Хэмминга

 

Пример: Построить макет кода Хемминга и определить значения корректирующих разрядов для кодовой комбинации k=4, X=0101.

Табл.7.3

<![if !vml]>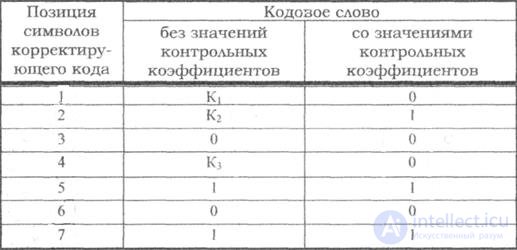<![endif]>

 

Решение:

Согласно таблице минимальное число контрольных символов r=3, при этом n = 7. Контрольный коэффициенты будут расположены на позициях 1, 2, 4. Составим макет корректирующего кода и запишем его во вторую колонку таблицы. Пользуясь таблицей для номеров проверочных коэффициентов, определим значения коэффициентов К1 К2 и К3.

Первая проверка: сумма П1+П3+П5+П7 должна быть четной, а сумма К1+0+1+1 будет четной при К =0.

Вторая проверка: сумма П2+П3+П6+П7 должна быть четной, а сумма К2+0+0+1 будет четной при К2=1.

Третья проверка: сумма П4+П5+П6+П7 должна быть четной, а сумма К3+1+0+1 будет четной при К3=0.

Окончательное значение искомой комбинации корректирующего кода записываем в третью колонку таблицы макета кода.

 

7.7 Обнаружение и исправление ошибок в коде Хэмминга.

 

Пример . Предположим, в канале связи под действием помех произошло искажение и вместо 0100101 было принято 01001(1)1.

Решение: Для обнаружения ошибки производят уже знакомые нам проверки на четность.

Первая проверка: сумма П1+П3+П5+П7 = 0+0+1+1 четна. В младший разряд номера ошибочной позиции запишем 0.

Вторая проверка: сумма П2+П3+П6+П7 = 1+0+1+1 нечетна. Во второй разряд номера ошибочной позиции запишем 1

Третья проверка: сумма П4+П5+П6+П7 = 0+1+1+1 нечетна. В третий разряд номера ошибочной позиции запишем 1. Номер ошибочной позиции 110= 6. Следовательно, символ шестой позиции следует изменить на обратный, и получим правильную кодовую комбинацию.

 

Код, исправляющий одиночную и обнаруживающий двойную ошибки

Табл.7.4

<![if !vml]>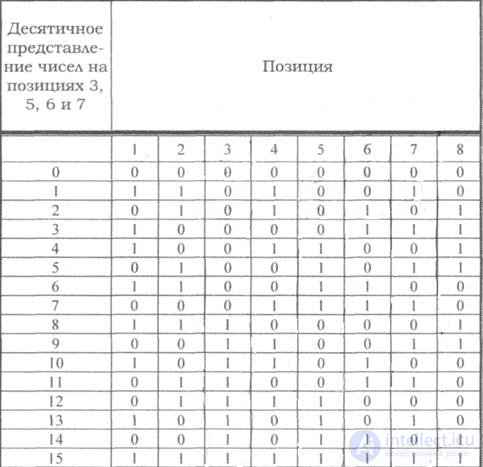<![endif]>

 

Если по изложенным выше правилам строить корректирующий код с обнаружением и исправлением одиночной ошибки для равномерного двоичного кода, то первые 16 кодовых комбинаций будут иметь вид, показанный в таблице. Такой код может быть использован для построения кода с исправлением одиночной ошибки и обнаружением двойной.

Для этого, кроме указанных выше проверок по контрольным позициям, следует провести еще одну проверку на четность для всей строки в целом. Чтобы осуществить такую проверку, следует к каждой строке кода добавить контрольные символы, записанные в дополнительной колонке (таблица, колонка 8). Тогда в случае одной ошибки проверки по позициям укажут номер ошибочной позиции, а проверка на четность - на наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ее, значит в кодовой комбинации две ошибки.

 

7.8 Контрольные вопросы.

1. Общий метод построения линейного кода.

2. Требования к образующей матрице.

3. Что такое проверочная матрица ТПМ?

4. В чем преимущество метода кодирования Хемминга?

5. Сколько ошибок может исправить код Хемминга

Надеюсь, эта статья про линейные коды общие методы построения, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое линейные коды общие методы построения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.