Лекция
Привет, сегодня поговорим про кодирование длин повторений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое кодирование длин повторений, дифференциальное кодирование , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.
Кодирование длин участков (или повторений) может быть достаточно эффективным при сжатии двоичных данных, например, черно-белых факсимильных изображений, черно-белых изображений, содержащих множество прямых линий и однородных участков, схем и т.п. Кодирование длин повторений является одним из элементов известного алгоритма сжатия изображений JPEG.
Идея сжатия данных на основе кодирования длин повторений состоит в том, что вместо кодирования собственно данных подвергаются кодированию числа, соответствующие длинам участков, на которых данные сохраняют неизменное значение.
Предположим, что нужно закодировать черно-белое(двухцветное) изображение размером 8 х 8 элементов, приведенное на рис. 14.1

Рис. 14.1
Просканируем это изображение по строкам (двум цветам на изображении будут соответствовать 0 и 1),в результате получим двоичный вектор данных
X= (0111000011110000000100000001000000010000000111100011110111101111)
длиной 64 бита (исходный код составляет 1 бит на элемент изображения).
Выделим в векторе X участки, на которых данные сохраняют неизменное значение, и определим их длины. Результирующая последовательность длин участков-положительных целых чисел, соответствующих исходному вектору данных X, -будет иметь видr = (1, 3, 4, 4, 7, 1, 7, 1, 7, 1, 7, 4, 3, 4, 1, 4, 1, 4).
Теперь эту последовательность, в которой заметна определенная повторяемость (единиц и четверок гораздо больше, чем других символов),можно закодировать каким-либо статистическим кодом, например, кодом Шеннона-Фано без памяти, имеющим таблицу кодирования (табл. 15.1)
Таблица 14.1
|
Кодер |
|
|
Длина участка |
Кодовое слово |
|
4 |
0 |
|
1 |
10 |
|
7 |
110 |
|
3 |
111 |
Для того, чтобы указать, что кодируемая последовательность начинается с нуля, добавим в начале кодового слова префиксный символ 0. Об этом говорит сайт https://intellect.icu . В результате получим кодовое слово B (r) = ( 0100011010110101101011001110100100 ) длиной в 34 бита, то есть результирующая скорость кода R составит 34/64, или немногим более 0,5 бита на элемент изображения. При сжатии изображений большего размера и содержащих множество повторяющихся элементов эффективность сжатия может оказаться существенно более высокой.
Существует еще один метод использования кодирования длин повторений, когда в цифровых данных встречаются участки с большим количеством нулевых значений. Всякий раз, когда в потоке данных встречается “ноль”, он кодируется двумя числами. Первое - 0, являющееся флагом начала кодирования длины потока нулей, и второе – количество нулей в очередной группе. Если среднее число нулей в группе больше двух, будет иметь место сжатие. С другой стороны, большое число отдельных нулей может привести даже к увеличению размера кодируемого файла:
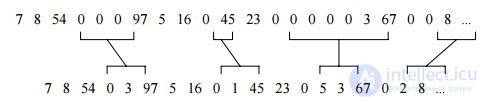
Еще одним простым и широко используемым для сжатия изображений и звуковых сигналов методом кодирования без потерь является метод дифференциального кодирования.
Работа дифференциального кодера основана на том факте, что для многих типов данных разница между соседними отсчетами относительно невелика, даже если сами данные имеют большие значения. Например, нельзя ожидать большой разницы между соседними пикселами цифрового изображения например для пейзажной, бытовой или жанровой фотографии. Другое дело, если мы фотографируем штрих-код или стадо зебр.
Следующий простой пример показывает, какое преимущество может дать дифференциальное кодирование (кодирование разности между соседними отсчетами) в сравнении с простым кодированием без памяти (кодированием отсчетов независимо друг от друга).
Просканируем 8-битовое (256-уровневое) цифровое изображение, и пусть при этом десять последовательных пикселов имеют уровни:
144, 147, 150, 146, 141, 142, 138, 143, 145, 142.
Если закодировать эти уровни пиксел за пикселом каким-либо кодом без памяти, использующим8 бит на пиксел изображения, получим кодовое слово, содержащее 80 бит.
Предположим теперь, что прежде чем подвергать отсчеты изображения кодированию, мы вычислим разности между соседними пикселами. Эта процедура даст нам последовательность следующего вида:
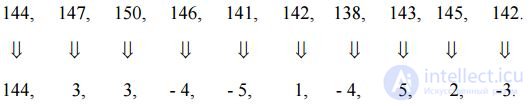
Исходная последовательность может быть легко восстановлена из разностной простым суммированием(дискретным интегрированием):

Для кодирования первого числа из полученной последовательности разностей отсчетов, как и ранее, понадобится 8 бит, все остальные числа можно закодировать 4-битовыми словами (один знаковый бит и 3 бита на кодирование модуля числа ).
Таким образом, в результате кодирования получим кодовое слово длиной 8+9*4=44 бита или почти вдвое более короткое, нежели при индивидуальном кодировании отсчетов.
Метод дифференциального кодирования очень широко используется в тех случаях, когда природа данных такова, что их соседние значения незначительно отличаются друг от друга, при том, что сами значения могут быть сколь угодно большими.
Это относится к звуковым сигналам, особенно к речи, изображениям, соседние пикселы которых имеют практически одинаковые яркости и цвет и т.п. В то же время этот метод совершенно не подходит для кодирования текстов, чертежей или каких-либо цифровых данных с независимыми соседними значениями.
Надеюсь, эта статья про кодирование длин повторений, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое кодирование длин повторений, дифференциальное кодирование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования
Из статьи мы узнали кратко, но содержательно про кодирование длин повторенийОтветы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Теория информации и кодирования
Термины: Теория информации и кодирования