Эффективное кодирование. кратко

Сразу хочу сказать, что здесь никакой воды про эффективное кодирование , и только нужная информация. Для того чтобы лучше понимать что такое эффективное кодирование , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

эффективное кодирование – это процедуры направленные на устранение избыточности. Основная задача эффективного кодирования – обеспечить, в среднем, минимальное число двоичных элементов на передачу сообщения источника. В этом случае, при заданной скорости модуляции обеспечивается передача максимального числа сообщений, а значит максимальная скорости передачи информации.

Пусть имеется источник дискретных сообщений, алфавит которого 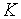. При кодировании сообщений данного источника двоичным, равномерным кодом, потребуется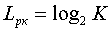двоичных элементов на кодирование каждого сообщения.

Если вероятности 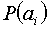появления всех сообщений источника равны, то энтропия источника (или среднее количество информации в одном сообщении) максимальна и равна.

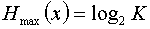В данном случае каждое сообщение источника имеет информационную емкость 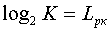бит, и очевидно, что для его кодирования (перевозки) требуется двоичная комбинация не менее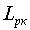элементов. Каждый двоичный элемент, в этом случае, будет переносить 1 бит информации.

Если при том же объеме алфавита сообщения не равновероятны, то, как известно, энтропия источника будет меньше

.

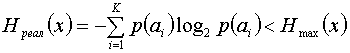Если и в этом случае использовать для перевозки сообщения -разрядные кодовые комбинации, то на каждый двоичный элемент кодовой комбинации будет приходиться меньше чем 1 бит.

Появляется избыточность, которая может быть определена по следующей формуле

.

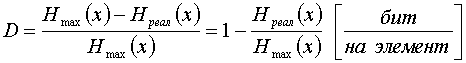+Среднее количество информации, приходящееся на один двоичный элемент комбинации при кодировании равномерным кодом

Под избыточностью понимают использование большого числа символов, чем минимально необходимо. Огромной избыточностью обладает язык. Возникает вопрос, как построить правило Г таким образом, чтобы избыточность была минимальной. Требования для построения неизбыточных (эффективных) кодов. Об этом говорит сайт https://intellect.icu . Чем больше вероятность появления сообщения, тем меньше должна быть его длина. Получим математическое соотношение, связывающее вероятность появления и длину соответствующей кодовой комбинации.

Пусть кодирующее отображение X={x₁,x₂,…,x_r}, это B, а |m| мощность.

Кодирующее отображение В каждому x_i ставит в соответствие некоторую кодовую комбинацию длительностью n_i из алфавита В. Задача: Оценить минимальную среднюю длину кодовой комбинации кода Г. Зная эту величину и сравнивая ее со средней длиной кодового слова реального кода, можно определить, насколько реально код близок к оптимальному. Известна вероятность P(x_i), и энтропия равна H(x)= -∑[i=1, k] P(x_i)*log₂P(x_i), Средняя длина n_ср=∑_i=1^rP_i*n_i. Максимальная энтропия, которую может иметь сообщение из символов алфавита В: H_max=n_ср*log₂m, т.к. H_max≥H(x), то n_ср*log₂m ≥ -∑_i=1^r P(x_i)*log₂P(x_i). Рассмотрим частный случай, при котором избыточность = 0. (H(x)=H_max), k_i — коэффициент избыточности.

k_i=(H_max — H(x))/H_max), k_i=(n_ср - n_min). ∑_i=1^r n_i*P(x_i)*log₂ m =-∑[i=1, r] P(x_i) log₂ P(x_i), ∑_i=1^r(P(x_i)*(n_ilog₂m+log₂P(x_i))=0, n_i log₂ m + log₂ P(x_i)=0, n_i= -log₂(P(x_i))/log₂m (*). Из (*) следует, что длина i-ой кодовой комбинации ~ (-log) вероятности появления i-го сообщения. Левая часть — целое число, правая часть — чаще всего нецелое. Полученное условие для реал. построения эффективного кода не может быть использовано, т.к. все равенство не выполняется. Но можно потребовать, чтобы n_i лежало в некотором диапазоне полученного значения, в котором обязательно найдется одно целое.

- log₂P(x_i)/log₂m ≤ n_i ≤ (- log₂P(x_i)/log₂(m)) +1, умножим обе части на P(x_i) …. - ∑_i=1^rP(x_i)log₂ P(x_i)/log₂m ≤ ∑_i=1^rP(x_i)n_i ≤ (-∑_i=1^rP(x_i)*log₂P(x_i)/log₂ m)+ ∑_i=1^rP(x_i),

H(x)/log₂m≤nср≤(H(x)/log₂ m)+1 (**).

Используя это неравенство можно численно оценить структурность построенного кода. Для получения эффективных кодов близких к нулю существует несколько методов (код Хаффмана, код Шеннона-Фано).

Пример: Для кодирования 32 букв русского алфавита, при условии равновероятности, нужна 5 разрядная кодовая комбинация. При учете ВСЕХ статистических связей реальная энтропия составляет около 1,5 бит на букву. Нетрудно показать, что избыточность в данном случае составит

,

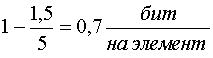Если средняя загрузка единичного элемента так мала, встает вопрос, нельзя ли уменьшить среднее количество элементов необходимых для переноса одного сообщения и как наиболее эффективно это сделать?

Для решения этой задачи используются неравномерные коды.

При этом, для передачи сообщения, содержащего большее количество информации, выбирают более длинную кодовую комбинацию, а для передачи сообщения с малым объемом информации используют короткие кодовые комбинации.

Учитывая, что объем информации, содержащейся в сообщении, определяется вероятностью появления

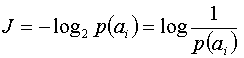, можно перефразировать данное высказывание.

Для сообщения, имеющего высокую вероятность появления, выбирается более короткая комбинация и наоборот, редко встречающееся сообщение кодируется длинной комбинацией.

Т.о. на одно сообщение будет затрачено в среднем меньшее единичных элементов 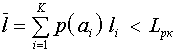, чем при равномерном.

Если скорость телеграфирования постоянна, то на передачу одного сообщения будет затрачено в среднем меньше времени

А значит, при той же скорости телеграфирования будет передаваться большее число сообщений в единицу времени, чем при равномерном кодировании, т.е. обеспечивается большая скорость передачи информации.

Каково же в среднем минимальное количество единичных элементов требуется для передачи сообщений данного источника? Ответ на этот вопрос дал Шеннон.

Шеннон показал, что

1. Нельзя закодировать сообщение двоичным кодом так, что бы средняя длина кодового слова была численно меньше величины энтропии источника сообщений., где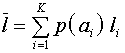

2. Существует способ кодирования, при котором средняя длина кодового слова немногим отличается от энтропии источника

Остается выбрать подходящий способ кодирования.

Эффективность применения оптимальных неравномерных кодов может быть оценена:

1. Коэффициентом статистического сжатия, который характеризует уменьшение числа двоичных элементов на сообщение, при применении методов эффективного кодирования в сравнении с равномерным 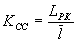. Учитывая, что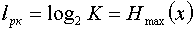, можно записать. Ксс лежит в пределах от 1 - при равномерном коде до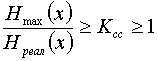, при наилучшем способе кодирования.

2. Коэффициент относительной эффективности

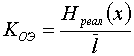- позволяет сравнить эффективность применения различных методов эффективного кодирования.

В неравномерных кодах возникает проблема разделения кодовых комбинаций. Решение данной проблемы обеспечивается применением префиксных кодов.

Вау!! 😲 Ты еще не читал? Это зря!

• Префиксный код
• Метод Хаффмена
• Арифметическое кодирование

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про эффективное кодирование Надеюсь, что теперь ты понял что такое эффективное кодирование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования

Из статьи мы узнали кратко, но содержательно про эффективное кодирование