6.1 Корректирующие свойства кодов с избыточностью.

Привет, сегодня поговорим про корректирующие свойства кодов с избыточностью , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое корректирующие свойства кодов с избыточностью , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

Лекция 6

6.1 корректирующие свойства кодов с избыточностью .

Рассмотрим сущность помехоустойчивого кодирования на уже рассмотренном на предыдущей лекции рисунке

<![if !vml]><![endif]>

Рис.6.1

На этом рисунке через Ai (N шт.)обозначенные разрешенные кодовые слова, Bj (L-N)шт.запрещенные слова, а Mi (Nшт.) некоторые подмножества, элементами которых являются те или другие запрещенные кодовые слова.

Из рисунка видно, что при передаче кодовой комбинации Ai она может под воздействием помех перейти в одну из комбинаций Bj, то есть ошибка может быть выявлена (L-N) случаях из общего количества L кодовых слов. Так происходит каждый раз, когда передается любая из N разрешенных кодовых комбинаций. Общее количество ошибочных комбинаций, которые обнаруживаются , равняется N(L-1)а общее количество возможных комбинаций L*N поэтому часть ошибочных комбинаций, которые обнаруживаются , равняется

µ=1-(N/L);

Аналогичный прием используется и для исправления ошибок. Для использования кода как корректирующего надо разбить множества Bj всего (L-N)шт.запрещенных кодовых комбинаций -на N непересекающихся подмножеств Mi. Каждое из подмножеств Mi приписывается одному из кодовых слов Ai . Способ корректировки или исправления ошибок заключается в том, что когда принятая комбинация Bj принадлежит Мi, тогда считается, что передана комбинация Аi. При таком способе декодирования существует возможность исправления ошибок.

Из рисунка видно, что при любом способе разбития ошибка может быть исправлена в L-N (для Bj) случаях и обнаружена в N(L-N)случаях. Отношение количества ошибочных комбинаций, которые исправляются, к количеству ошибочных комбинаций равно 1/N.

Наконец, определим, что количество -ошибок, которые не исправляются равняется N*(N-1) ,при этом часть некорректируемых ошибок по отношению к общему количеству последствий равняется (N-1)/L. Отмеченные результаты имеют общий характер и верныдля всех корректирующих кодов.

Мы говорили о корректирующих свойствах кодов с избыточностью.

Рассмотрим теперь простые примеры, которые связывают кодовое расстояние d с корректируюшими свойствами кода.

Очевидно, что при кодовом расстоянии d=1 все кодовые комбинации являются разрешенными.

Например, при n=3 разрешенные комбинации образуют следующее множество:

000,001,010,011, 100, 101, 110, 111 с кодовым расстоянием d=1.

Любая одиночная ошибка трансформирует данную комбинацию в другую разрешенную комбинацию. Это случай безызбыточного кода, не обладающего корректирующей способностью.

Если d = 2, то ни одна из разрешенных кодовых комбинаций при одиночной ошибке не переходит в другую разрешенную комбинацию. Например, подмножество разрешенных кодовых комбинаций может быть образовано по принципу четности в нем числа единиц. Например, для n=3, d=2:

011, 101, 110-разрешенные комбинации;

010, 100, 111 - запрещенные комбинации.

При любой одиночной ошибке разрешенная комбинация превращается в запрещенную. Код обнаруживает одиночные ошибки, а также другие ошибки нечетной кратности .

В общем случае при необходимости обнаруживать ошибки кратности до г включительно минимальное хэммингово расстояние между разрешенными кодовыми комбинациями должно быть по крайней мере на единицу больше r, т.е d >r+1.

Действительно, в этом случае ошибка, кратность которой не превышает r, не в состоянии перевести одну разрешенную кодовую комбинацию в другую.

Для исправления одиночной ошибки кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций множеству исходных кодовых комбинаций.

Чтобы эти подмножества не пересекались, хэммингово расстояние между разрешенными кодовыми комбинациями должно быть не менее трех. Об этом говорит сайт https://intellect.icu . При n=3 за разрешенные кодовые комбинации можно, например, принять 000 и 111 с d=3. Тогда разрешенной комбинации 000 необходимо приписать подмножество запрещенных кодовых комбинаций 001, 010, 100, образующихся в результате двоичной ошибки в комбинации 000.

Подобным же образом разрешенной комбинации 111 необходимо приписать подмножество запрещенных кодовых комбинаций: 110, 011, 101, образующихся в результате возникновения единичной ошибки в комбинации 111:

Разрешенной комбинации 000 соответствуют запрещенные комбинации 001 010 100.

Если принято любое кодовое слово из этого набора, то по принципу максимального правдоподобия можно предположить, что передавалось кодовое слово 000.

Разрешенной комбинации 111 соответствуют запрещенные комбинации 011 101 110.

Если принято любое кодовое слово из этого набора, то по принципу максимального правдоподобия передавалось кодовое слово 111.

Таким образом для кода 000 и 111 с d=3 может быть исправлена одна ошибка.

В общем случае для обеспечения возможности исправления всех ошибок кратности до s включительно каждая из ошибок должна приводить к запрещенной комбинации, относящейся к подмножеству исходной разрешенной кодовой комбинации.

Ошибка будет не только обнаружена, но и исправлена, если искаженная комбинация остается ближе к первоначальной, чем к любой другой разрешенной комбинации, то есть должно быть:

d>=2S+1;

Рассмотрим геометрическую интерпретацию кодового расстояния d и его связь с числом обнаруживаемых и исправляемых ошибок.

Для выявления произвольных ошибок, которые изменяют в кодовых словах, , не больше r символов, необходимо и достаточно, чтобы никакие r-кратные ошибки не переводили одно кодовое слово кода в другое, смотри рисунок 6.2

<![if !vml]><![endif]>

Рис.6.2

Это условие будет выполнено, если кодовые комбинации выбраны так, что среди них нет таких, которые находятся на расстоянии, меньше чем r+1. Если такой код использован для кодировки сообщения, тогда принятое кодовое слово Y, которого нет в списке разрешенных слов, является признаком обнаружением ошибки. Рассмотренные ранее 4 комбинации -000, 011, 101, 110,- представляют код с обнаружением одиночной ошибки, потому что для них кодовое расстояние d = 2. Для того, чтобы код исправлял все ошибки, кратность которых не превосходит s,.векторы каждой пары Xi, Xj должны находиться один от другого на расстоянии, не меньшем чем 2s+1.

В общем случае для выявления ошибок кратности r, одновременного исправления ошибок кратности s необходимо и достаточно выполнение условия

d>=r+s+1.

Кодовое расстояние лишь частично характеризует качество кода, потому что кроме ошибок, которые полностью исправляются или обнаруживаются, часто обнаруживаются или исправляются ошибки большей кратности.

Рассмотрим понятие качества корректирующего кода более подробно.

Одной из основных характеристик корректирующего кода является избыточность кода, указывающая степень удлинения кодовой комбинации для достижения определенной корректирующей способности.

Если на каждые n символов выходной последовательности кодера канала приходится k информационных и r проверочных, то относительная избыточность кода может быть выражена как:

ρ =(n-k)/n=r/n=0…1;

Коды, обеспечивающие заданную корректирующую способность при минимально возможной избыточности, называют оптимальными.

В связи с нахождением оптимальных кодов оценим, например, возможное наибольшее число Q разрешенных или информационных комбинаций n-значного двоичного кода, обладающего способностью исправлять взаимно независимые ошибки кратности до s включительно. Это равносильно отысканию числа комбинаций, кодовое расстояние между которыми не менее d=2s+l.

Общее число различных исправляемых ошибок для каждой разрешенной комбинации составляет

_{<![if !vml]>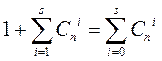<![endif]>}

где С_nⁱ- число ошибок кратности i<s.

Каждая из таких ошибок должна приводить к запрещенной комбинации, входящей в подмножество Mi для данной разрешенной комбинации. Совместно с этой разрешенной комбинацией подмножество включает всего вот столько комбинаций.

_{<![if !vml]>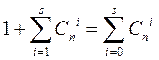<![endif]>}

Однозначное декодирование возможно только в том случае, когда указанные подмножества не пересекаются. Так как общее число различных комбинаций n- значного двоичного кода составляет 2ⁿ, то число разрешенных комбинаций не может превышать

_{<![if !vml]>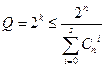<![endif]>}

Эта верхняя оценка найдена Хэммингом. Для некоторых конкретных значений кодового расстояния d, соответствующие Q укажем в таблице:

Таблица 6.1

<![if !vml]>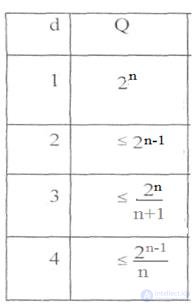<![endif]>

Коды, для которых в приведенном соотношении достигается равенство, называют также плотно упакованными.

Однако не всегда целесообразно стремиться к использованию кодов, близких к оптимальным. Необходимо учитывать другой, не менее важный показатель качества корректирующего кода - сложность технической реализации процессов кодирования и декодирования. Здесь должен искаться компромисс между корректирующими свойствами кода и сложностью технической реализации.

Если информация должна передаваться но медленно действующей и дорогостоящей линии связи, а кодирующее и декодирующее устройства предполагается выполнить на высоконадежных и быстродействующих элементах, то сложность этих устройств не играет существенной роли. Решающим фактором в этом случае является повышение эффективности пользования линией связи, поэтому желательно применение корректирующих кодов с минимальной избыточностью.

Если же корректирующий код должен быть применен в системе, выполненной на элементах, надежность и быстродействие которых равны или близки надежности и быстродействию элементов кодирующей и декодирующей аппаратуры. Это возможно, например, для повышения достоверности воспроизведения информации с запоминающего устройства ЭВМ. Тогда критерием качества корректирующего кода является надежность системы в целом, то есть с учетом возможных искажений и отказов в устройствах кодирования и декодирования. В этом случае часто более целесообразны коды с большей избыточностью, но простые в технической реализации.

6.2 Классификация корректирующих кодов.

Общая классификация, удобная с точки зрения следующего изучения важнейших классов кодов, представлена на рисунке 6.3

<![if !vml]>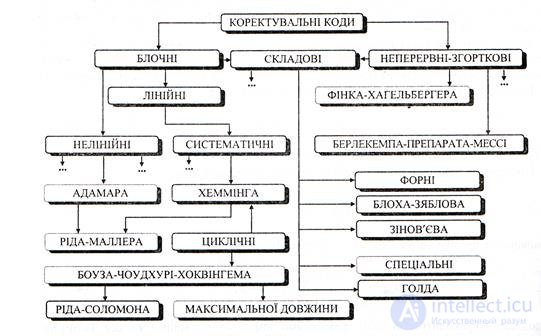<![endif]>

Рис.6.3

Корректирующие коды можно разделить на два больших класса: блочные и непрерывные.

Блочные коды состоят из отдельных комбинаций (блоков), которые кодируются и декодируются независимо.

Непрерывные или сверточные коды представляют непрерывную последовательность кодовых символов, ее разделения на отдельные кодовые комбинации не проводится.. Название этих кодов происходит от того что исходная последовательность непрерывного кода представляет свертку входной информационной последовательности с импульсной характеристикой кода. Составные(комбинированные, производные, коды произведений, специальные и др.) корректирующие коды строят на основе блочных или блочного и непрерывного кодов. Эти коды называют также каскадными кодами .

Блочный код называют линейным, если все его кодовые слова образуют линейное векторное пространство. Таким образом, новую разрешенную комбинацию кода можно получить как линейную комбинацию других разрешенных кодовых слов, в противоположном случае код называют нелинейным. Систематическим называют код, в котором кодовые слова состоят из kинформационных и r проверочных символов, при этом позиции информационных и проверочных символов одни и те же для всех кодовых слов кода. Такое формирование кодовых комбинаций существенно упрощает техническую реализацию устройства кодировки и декодирования. Поэтому систематические коды являются одними из наиболее распространенных.

Под классом линейных (систематических) кодов являются коды Хемминга и циклические коды, например, коды Боуза-Чоудхури- Хоквингема (БЧХ-коды). Редким случаем БЧХ-кодов являются коды максимальной длины (М-последовательности). По установленной традиции ряд подклассов коррекционных кодов помечают фамилиями тех ученых, которые впервые предложили и исследовали тот или другой вид кодировки.

Особенности построения и характеристики многих кодов, выделенных на рисунке является предметом дальнейшего рассмотрения.

6.3 Контрольные вопросы.

1. Чем отличается обнаружение ошибки от ее исправления?

2. Связь кодового расстояния с числом обнаруживаемых ошибок.

3. Связь кодового расстояния с числом исправляемых ошибок.

4. В чем смысл оценки Хемминга для объема кода с заданным кодовым расстоянием?

Надеюсь, эта статья про корректирующие свойства кодов с избыточностью , была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое корректирующие свойства кодов с избыточностью и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.