Перплексия в теории информации кратко

Привет, Вы узнаете о том , что такое перплексия, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое перплексия , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

В теории информации , перплексия - это измерением того , насколько хорошо распределение вероятностей или вероятностная модель предсказывает образец. Его можно использовать для сравнения вероятностных моделей. Низкое Перплексия указывает на то, что распределение вероятностей хорошо предсказывает выборку.

Учитывая две вероятностные модели, лучшая модель - это та, которая лучше соответствует тестовым данным • вероятность, которую модель присваивает тестовым данным; лучшая модель назначит более высокую вероятность тестовым данным

Наиболее распространенным внутренним критерием является перплексия (perplexity), используемая для оценивания моделей языка в вычислительной лингвистике. Это мера несоответствия или «удивленности» модели p(w | d) токенам w, наблюдаемым в документах d коллекции D.

Она определяется через логарифм правдоподобия (2.18), отдельно для каждой модальности:

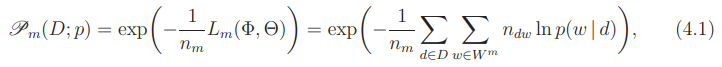
где — длина коллекции по m-й модальности.

Чем меньше величина перплексии, тем лучше модель p предсказывает появление токенов w в документах d коллекции D.

Перплексия имеет следующую интерпретацию. Если термины w порождаются из равномерного распределения p(w) = 1/V на словаре мощности V , то перплексия модели p(w) на таком тексте сходится к V с ростом его длины. Чем сильнее распределение p(w) отличается от равномерного, тем меньше перплексия. Чем сильнее модель p(w) отличается от генерирующего распределения, тем больше перплексия. В случае условных вероятностей p(w | d) интерпретация немного другая: если каждый документ генерируется из V равновероятных терминов (возможно, различных в разных документах), то перплексия сходится к V .

Обозначим через pD(w | d) модель, построенную по обучающей коллекции документов D. Перплексия обучающей выборки является оптимистично смещенной (заниженной) характеристикой качества модели из-за эффекта переобучения. Обобщающую способность тематических моделей принято оценивать перплексией контрольной выборки (hold-out perplexity) 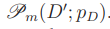коллекцию разделяют на обучающую и контрольную случайным образом в пропорции 9 : 1 [17].

Перплексия вероятностного распределения

Сложность PP дискретного распределения вероятностей p определяется как

где H ( p ) - энтропия (в битах) распределения, а x варьируется по событиям. (База не обязательно должна быть 2: Перплексия не зависит от базы, при условии, что энтропия и возведение в степень используют одно и то же основание.) Эта мера также известна в некоторых областях как разнообразие (истинного порядка 1) .

Сложность случайной величины X может быть определена как сложность распределения ее возможных значений x .

В частном случае, когда p моделирует справедливый k- сторонний кубик (равномерное распределение по k дискретным событиям), его сложность равна k . Случайная величина недоумения к имеет такую же неопределенность как справедливо K односторонний фильер, и один называется « K -ways недоумевает» о значении случайной величины. Об этом говорит сайт https://intellect.icu . (Если это не справедливый k- сторонний кубик, будет возможно более k значений, но общая неопределенность не больше, потому что некоторые из этих значений будут иметь вероятность больше 1 / k , уменьшая общее значение при суммировании.)

Перплексия иногда используется как мера того, насколько сложна проблема прогнозирования. Это не всегда верно. Если у вас есть два варианта, один с вероятностью 0,9, то ваши шансы на правильное предположение составляют 90 процентов при использовании оптимальной стратегии. Перплексия составляет 2 ^{−0,9 log ₂ 0,9 - 0,1 log ₂ 0,1} = 1,38. Обратное значение недоумения (которое в случае правильного k-образного кубика представляет вероятность правильного угадывания) составляет 1 / 1,38 = 0,72, а не 0,9.

Перплексия заключается в возведении в степень энтропии, которая является более точной величиной. Энтропия - это мера ожидаемого или «среднего» количества битов, необходимых для кодирования результата случайной переменной, с использованием теоретического оптимального кода переменной длины, ср. Это также можно рассматривать как ожидаемый выигрыш информации от изучения результата случайной величины.

Перплексия вероятностной модели

Модель неизвестного распределения вероятностей p может быть предложена на основе обучающей выборки, взятой из p . Учитывая предложенную вероятностную модель q , можно оценить q , задав вопрос, насколько хорошо она предсказывает отдельный тестовый образец x ₁ , x ₂ , ..., x _N, также взятый из p . Сложность модели q определяется как

где обычно 2. Лучшие модели q неизвестного распределения p будут стремиться назначать более высокие вероятности q ( x _i ) тестовым событиям. Таким образом, у них меньше недоумения: они меньше удивляются тестовой выборке.

Вышеуказанный показатель степени можно рассматривать как среднее количество битов, необходимых для представления тестового события x _i, если используется оптимальный код, основанный на q . Модели с низкой степенью сложности лучше сжимают тестовую выборку, требуя в среднем нескольких бит на тестовый элемент, потому что q ( x _i ) имеет тенденцию быть большим.

Показатель также можно рассматривать как кросс-энтропию ,

где обозначает эмпирическое распределение тестовой выборки (т. е.если x встречается n раз в тестовой выборке размера N ).

Перплексия на слово

В обработке естественного языка Перплексия - это способ оценки языковых моделей . Языковая модель - это распределение вероятностей по целым предложениям или текстам.

Используя определение недоумения для вероятностной модели, можно, например, обнаружить, что среднее предложение x _i в тестовой выборке может быть закодировано в 190 бит (т. Е. Тестовые предложения имели среднюю логарифмическую вероятность -190). Это привело бы к огромному модельному недоумению - 2 ¹⁹⁰ на предложение. Однако более распространено нормализовать длину предложения и рассматривать только количество бит на слово. Таким образом, если предложения тестовой выборки содержат в общей сложности 1000 слов и могут быть закодированы с использованием в сумме 7,95 бит на слово, можно сообщить о затруднении модели 2 ^7,95 = 247 на слово. Другими словами, модель настолько запуталась в тестовых данных, как если бы ей пришлось выбирать единообразно и независимо среди 247 вариантов для каждого слова.

Самый низкий уровень недоумения, опубликованный в Brown Corpus (1 миллион слов американского английского разных тем и жанров) по состоянию на 1992 год, действительно составляет около 247 слов на слово, что соответствует перекрестной энтропии log ₂ 247 = 7,95 бит на слово или 1,75 бит на букву с использованием модели триграммы . Часто можно добиться меньшего недоумения на более специализированных корпусах , поскольку они более предсказуемы.

Опять же, простое предположение о том, что следующим словом в корпусе Брауна является слово «the», будет иметь точность 7 процентов, а не 1/247 = 0,4 процента, поскольку наивное использование недоумения в качестве меры предсказуемости может привести к мысли . Это предположение основано на статистике униграммы корпуса Брауна, а не на статистике триграммы, которая дала словесное Перплексия 247. Использование статистики триграммы еще больше повысило бы шансы на правильное предположение.

Ограничение применения

Недостатком перплексии является неочевидность ее численных значений, а также ее зависимость не только от качества модели, но и от ряда посторонних факторов — длины документов, мощности и разреженности словаря. В частности, с помощью перплексии некорректно сравнивать тематические модели одной и той же коллекции, построенные на разных словарях.

Недостатком контрольный перплексии является высокая чувствительность к редким и новым словам, которые практически бесполезны для тематических моделей. В ранних экспериментах было показано, что LDA существенно превосходит PLSA по перплексии, откуда был сделан вывод, что LDA меньше переобучается [17]. В [2, 5, 3] были предложены робастные тематические модели, описывающие редкие слова специальным «фоновым» распределением. Перплексия робастных вариантов PLSA и LDA оказалась существенно меньшей и практически одинаковой

Применение

Перплексия — это очень известная в вычислительной лингвистике мера качества модели языка. В лингвистике оценкой качества языковой модели служит перплексия (perplexity) — мера того, насколько хорошо модель предсказывает детали тестовой коллекции (чем меньше перплексия, тем лучше модель). Существует несколько способов оценки качества тематических моделей — наиболее распространенным критерием является перплексия, зависящая от мощности словаря и распределения частот слов в коллекции документов

.

Список литературы

Воронцов К. В. Аддитивная регуляризация тематических моделей коллекций текстовых документов // Доклады РАН. — 2014. — Т. 456, № 3. — С. 268–271.
Воронцов К. В., Потапенко А. А. Регуляризация, робастность и разреженность вероятностных
тематических моделей // Компьютерные исследования и моделирование. — 2012. — Т. 4, № 4. —
С. 693–706.
Воронцов К. В., Потапенко А. А. Модификации EM-алгоритма для вероятностного тематического моделирования // Машинное обучение и анализ данных. — 2013. — Т. 1, № 6. — С. 657–686.
Воронцов К. В., Потапенко А. А. Регуляризация вероятностных тематических моделей для
повышения интерпретируемости и определения числа тем // Компьютерная лингвистика и интеллектуальные технологии: По материалам ежегодной Международной конференции «Диалог» (Бекасово, 4–8 июня 2014 г.). — Вып. 13 (20). — М: Изд-во РГГУ, 2014. — С. 676–687.

Potapenko A. A., Vorontsov K. V. Robust PLSA performs better than LDA // 35th European Conference on Information Retrieval, ECIR-2013, Moscow, Russia, 24-27 March 2013. — Lecture Notes in Computer Science (LNCS), Springer Verlag-Germany, 2013. — Pp. 784–787

Вау!! 😲 Ты еще не читал? Это зря!

• Когерентность PMI
• Биграмма , триграмма

Выводы из данной статьи про перплексия указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое перплексия и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования