Кодирование,декодирование понятие, и элементы теории кодирования.

Привет, сегодня поговорим про кодирование, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое кодирование, декодирование, неравномерные коды , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

4.1 Общие понятия и элементы теории кодирования.

Определим некоторые понятия.

кодирование - операция отождествления символов или групп символов одного кода с группами символов другого кода.

Код это совокупность знаков и система определенных правил, при помощи которых информация может быть представлена или закодирована в виде набора этих знаков для передачи, обработки и хранения. Конечная последовательность кодовых знаков называется словом. Наиболее часто для кодирования информации используют буквы, ,цифры, знаки и их комбинации.

Рассмотрим обобщенную схему передачи цифровой информации

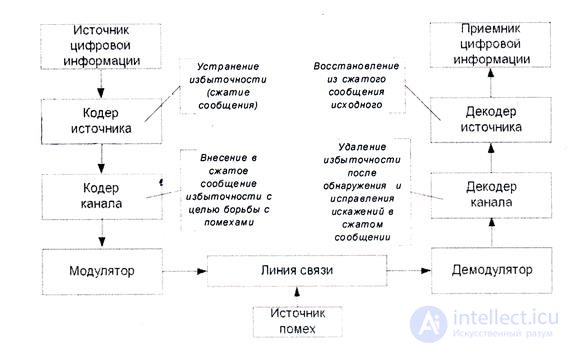
Рис.4.1 Обобщенная схема передачи цифровой информации

Рассматриваемые сегодня принципы кодирования информации справедливы как для систем, основная задача которых - передача информации в пространстве (системы связи), так и для систем, основная задача которых -передача информации во времени (системы хранения информации).

На вход кодера источника поступает последовательность символов, входящих во множество, называемое первичным алфавитом.

Кодер преобразует эту последовательность в другую, составленную чаще всего из других знаков, множество которых образует вторичный алфавит.

Если операции кодирования-декодирования выполняются компьютером и промежуточное представление информации человеку не требуется, эти алфавиты чаще всего состоят из 2 символов - 0 и 1. Это связано с особенностями современных цифровых устройств и их элементной базы.

Поскольку объем или число знаков вторичного алфавита меньше объема символов первичного алфавита , то при кодировании каждому символу или группе символов первичного алфавита ставится в соответствие группа символов вторичного алфавита, которую называют кодовой комбинацией . Число символов вторичного алфавита в кодовой комбинации называют ее длиной.

Коды, вторичный алфавит которых состоит из двух символов, обычно 0 и 1, называют двоичными.

Операция образования последовательности кодовых комбинаций по входной последовательности символов или комбинаций первичного алфавита называется кодированием. Выполняется кодирование при помощи кодера, который может быть устройством, программой или аппаратно-программным комплексом.

Обратная операция называется декодирование м и выполняется декодером.

Jungle Cars Trip Multiplayer - Invite your friends!

Game: Perform tasks and rest cool.7 people play!

Play game

4.2 Цели кодирования.

Решающий вклад в теорию передачи информации в конце 40-х годов, как известно, внес американский ученый Клод Шеннон. Он обосновал, в частности, эффективность ввода в систему передачи информации кодирующих-декодирующих устройств, основное назначение которых - согласование информационных свойств источника сообщений со свойствами канала связи.

Одно из них - кодер источника - обеспечивает такое кодирование, при котором путем устранения избыточности существенно уменьшается объем данных, передаваемых по каналу связи.

Такое кодирование называется эффективным или оптимальным.

Если в канале связи действуют помехи, это кодирование преобразует данные в форму, удобную для последующего помехоустойчивого кодирования.

Помехоустойчивое кодирование выполняется кодером канала. Его назначение следует из названия - борьба с искажениями, возникающими вследствие помех, действующих в канале связи.

Таким образом, при помощи кодера источника на основе статистических характеристик кодируемого сообщения уменьшается его объем, а при помощи кодера канала на основе статистических характеристик, действующих в канале помех, обеспечивается восстановление передаваемых через канал данных, даже если они искажены.

Такое разделение существенно упрощает исследование и проектирование кодеров-декодеров.

В случае малой избыточности можно отказаться от использования кодера-декодера источника. При малой же интенсивности помех в канале связи можно отказаться от помехоустойчивого кодирования и, соответственно от кодера-декодера канала.

Элементы теории кодирования

Некоторые общие свойства кодов .

Рассмотрим на примерах. Предположим, что дискретный источник выдающий на выходе сообщения , имеет алфавит из Nбукв или символов, поступающих с вероятностями p1, p2, …, pN.

Каждый символ кодируется с использованием вторичного алфавита из mбукв. Обозначим ni - число букв в кодовом слове, которое соответствует i-й букве источника. Нас будет интересовать средняя длина кодового слова пср, которая находится по известной формуле:

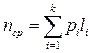
В качестве примера рассмотрим возможные способы составления кодовых слов двоичного кода при объеме первичного алфавита к=4

Таблица 4.1

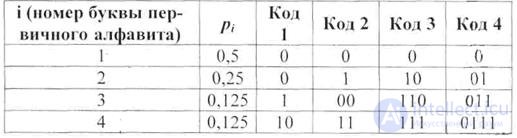
Заметим, что код 1 имеет неудачное свойство, состоящее в том, что буквы с номерами 1 и 2 кодируются одинаково - кодовым словом 0. Поэтому однозначное декодирование при использовании этого кода невозможно.

Код 2 обладает подобным же недостатком: последовательность из двух вторых букв первичного источникабудет закодирована в 00, что совпадает с кодовым словом для буквы 3. Затруднений для декодирования в этом случае не будет только тогда, когда между кодовыми словами будет добавлен какой-либо разделительный символ. Но если такой символ ввести, то его можно понимать как дополнительную букву вторичного алфавита. Тогда каждое кодовое слово в конце или в начале просто дополняется этой буквой. В результате такой код можно рассматривать как частный случай кодов без разделительных символов. Об этом говорит сайт https://intellect.icu . По этой причине коды с разделительными символами отдельно не рассматриваются.

Примером такого кода может служить код 4, где 0 можно, понимать как разделительный символ.

Из вышесказанного следует, что код является однозначно декодируемым, если кодовые слова, соответствующие различным буквам первичного алфавита, различны. Это необходимое условие однозначной декодируемости, однако не всегда достаточное.

С точки зрения теории и практики наиболее важными среди всех однозначно декодируемых кодов являются так называемые префиксные коды.

Префиксными называют коды, в которых каждое кодовое слово не является начальной частью или префиксом другого кодового слова. Это уже достаточное условие однозначной декодируемости.

Нетрудно заметить, что коды 1 и 2 не являются префиксными.

Вопросы :

• 1) являются ли коды 3 и 4 префиксными?
• 2) являются ли коды 3 и 4 однозначно декодируемыми?

Коды удобно описывать графически с помощью графа, называемого кодовым деревом. Это дерево строится из одной вершины и имеет узлы нулевого, первого, второго и т.д. порядков. Из каждого узла выходит т лучей - ребер, каждому из которых соответствует определенная буква вторичного алфавита.

На рис. 4.2. изображено кодовое дерево кода 3, описанного в таблице 4.1.

Рис. 4.2.

Каждому i-му кодовому слову длиной пi, ставится в соответствие узел xi, i-го порядка и определенный путь по кодовому дереву от корня до этого узла.

Из графического представления следует, что код будет префиксным, если узлы, соответствующие кодовым словам, являются концевыми, т.е. через них не лежит путь к другим узлам, также соответствующим кодовым словам.

4.3 Оптимальные неравномерные коды .

Определения.

Неравномерными называют коды, кодовые слова которых имеют различную длину.

Оптимальность можно понимать по-разному, в зависимости от критерия. В данном случае таким критерием является средняя длина кодового слова. Оптимальность с учетом этого критерия понимается в смысле минимальной длины средней длины кодового слова.

Дальнейшие выводы будем делать при следующих условиях:

Пусть буквы первичного источника a1 a2.,.., ак имеют вероятности появления p1, р2, ... , рк . Упорядочим буквы в порядке убывания вероятностей их появления в сообщении и пронумеруем их в этом порядке. В результате p1 > р2 >...> рк . Для кодирования будем использовать вторичный алфавит, состоящий из 2 букв - 0 и 1, т.е. двоичный код.

Пусть x1, х2, ... , хk - множество кодовых слов, имеющих длину n1, n2, ... , nk. Ограничимся также рассмотрением только префиксных кодов. Результаты, полученные в отношении длин кодовых слов для префиксных кодов, можно распространять на весь класс однозначно декодируемых кодов, а результаты, полученные для двоичных кодов можно обобщить на коды с любым объемом вторичного алфавита.

4.4 Коды Шеннона-Фэно.

Независимо друг от друга Шенноном и Фэно была предложена процедура построения эффективного кода. Получаемый при ее помощи код называют кодом Шеннона-Фэно.

Код Шеннона-Фэно строится следующим образом:

1) буквы алфавита сообщений выписываются в таблицу в порядке убывания вероятностей;

2) затем они разделяются на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы;

3) всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним буквам символ 0;

4) каждая из полученных групп, в свою очередь, разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д. ;

5) процесс повторяется до тех пор, пока в каждой подгруппе не останется по одной букве.

Рассмотрим первичный источник из восьми символов. Ясно, что при обычном (не учитывающем статистических характеристик) кодировании для представления каждой буквы требуется три символа. Пусть вероятности появления букв первичного источника равны:

p1=1/2; p2=1/4; p3=1/8; p4=1/16; p5=1/32; p==1/64; p7=1/128; p8=1/128/

Наибольший эффект сжатия получается в случае, когда вероятности букв представляют собой целочисленные отрицательные степени двойки. Среднее число символов на букву в этом случае точно равно энтропии.

Убедимся в этом, вычислив энтропию для нашего примера:

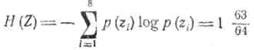
и среднее число символов на букву первичного алфавита.

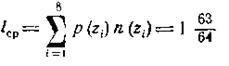
где n(zi) —число символов в кодовой комбинации , соответствующей букве zi. Характеристики такого ансамбля и коды букв представлены в таблице 4.2.

Таблица 4.2.

В более общем случае для алфавита из восьми букв среднее число символов на букву будет меньше трех, но больше энтропии алфавита H(Z). Для ансамбля букв, приведенного в следующей таблице для другого источника, энтропия равна 2,76, а среднее число символов на букву 2,84.

Таблица 4.3.

Следовательно, некоторая избыточность в последовательностях символов осталась. Из теоремы Шеннона следует, что эту избыточность также можно уменьшить, если перейти к кодированию достаточно большими блоками.

Рассмотрим сообщения, образованные с помощью алфавита, состоящего всего из двух букв Z1 и Z2, с вероятностями появления соответственно p(Z1)=0,9 и p(Z2) =0,1.

Поскольку вероятности не равны, то последовательность из таких букв будет обладать избыточностью. Однако при побуквенном кодировании Шеннона-Фано никакого эффекта не получается.

Действительно, на передачу каждой буквы требуется символ либо 1, либо 0, и nср.=1 в то время как энтропия равна 0,47.

При кодировании блоков, содержащих по две буквы, получим коды, показанные в таблице.

Таблица 4.4.

Так как буквы статистически не связаны, вероятности блоков определяются как произведение вероятностей составляющих букв.

Среднее число символов на блок получается равным 1,29; а на букву -0,645.

Кодирование блоков, содержащих по три буквы, дает еще больший эффект. Соответствующий ансамбль и коды приведены в таблице.

Таблица 4.5.

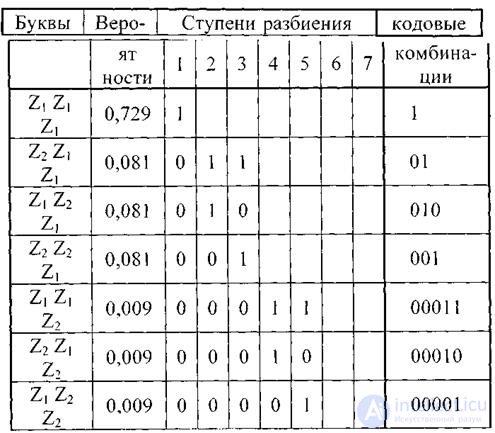
Среднее число символов на блок равно 1,59; а на букву - 0,53; что всего на 12% больше энтропии. Теоретический минимум H(Z) = 0,47 может быть достигнут при кодировании блоков, включающих бесконечное число букв:

lim lcp=H(Z), при m→∞

Следует подчеркнуть, что увеличение эффективности кодирования при укрупнении блоков, не связано с учетом все более далеких статистических связей, так как нами рассматривались алфавиты с некоррелированными буквами. Повышение эффективности определяется лишь тем, что набор вероятностей, получающийся при укрупнении блоков, можно делить на более близкие по суммарным вероятностям подгруппы.

Рассмотренная нами методика Шеннона—Фэно не всегда приводит к однозначному построению кода. В методике присутствует элемент субъективизма. Ведь при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу.

Поэтому конкретный полученный код может оказаться не самым лучшим. При построении эффективных кодов с основанием т>2 неопределенность разделения на группы становится еще большей.

От указанного недостатка свободна методика Хаффмена. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

4.5 Коды Хаффмена.

На этом алгоритме построена процедура построения оптимальною кода, предложенная в 1952 году Хаффменом:

1)буквы первичного алфавита выписываются в основной столбец в порядке убывания вероятностей;

2) две последние буквы объединяются в одну вспомогательную букву, которой приписывается суммарная вероятность;

3) вероятности букв, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются;

3) процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Методика поясняется примером.

Таблица 4.6

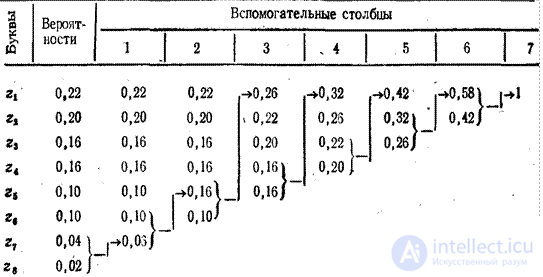
Для составления кодовой комбинации, соответствующей конкретному символу, следует проследить путь перехода вероятности символа по строкам и столбцам таблицы.

Для наглядности при построении кода строится кодовое дерево. Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваивается символ 1, а с меньшей - 0. Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до каждой буквы. Кодовое дерево для алфавита букв, рассматриваемого в таблице, изображено на рисунке 4.2.

Рис.4.3

Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию (см.таблицу 4.7).

Таблица 4.7

Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8
01	00	111	110	100	1011	10101	10100

4.6 Особенности эффективных кодов.

1. Букве первичного алфавита с наименьшей вероятностью появления ставится в соответствие код с наибольшей длиной , т.е. такой код является неравномерным (с разной длиной кодовых слов). В результате, если моментами передачи сообщения от источника приемник управлять не может (например, кодовые слова поступают строго периодически с шагом ∆t), через линию связи будут передаваться кодовые слова с разной длиной, т.е. количество передаваемых в единицу времени через линию связи букв вторичного алфавита будет меняться. Учитывая то, что любая линия связи характеризуется максимальной скоростью передачи информации (пропускной способностью), приходим к выводу, что при использовании такой схемы передачи информации пропускная способность линии связи будет использоваться не в полной мере. Избежать неэффективного использования линии связи можно, установив на ее входе и выходе буферные накопительные запоминающие устройства. Они позволяют сгладить неравномерность поступления букв вторичного алфавита как через линию связи, так и на вход декодирующего устройства. При этом во всей системе передачи информации возникают временные задержки и, чем объем буферного устройства выше, тем эти задержки выше.

2. Вторая особенность связана с временными задержками в передаче информации, возникающими при использовании кодирования блоков букв первичного алфавита, которые, позволяют увеличить эффективность кода (уменьшить среднюю длину кодового слова). Кодирование блоков букв первичного алфавита требует их предварительного накопления. Отсюда и возникающие временные задержки.

3. Третья особенность заключается в том, что, как оказывается, эффективные коды не предназначены для использования в условиях помех. Если же все-таки по какой-либо причине, например, в результате электрической помехи от грозового разряда, какой-то символ кодового слова исказится, правильное декодирование становится невозможным не только для этого кодового слова, но и для целого ряда следующих за ним кодовых слов.

Возникает так называемый трек ошибки. Таким образом, улучшив одну из качественных характеристик кода, в данном случае среднюю длину кодового слова пср, ухудшается другая характеристика -устойчивость к воздействию помех. Эффективные коды надо использовать либо в условиях полного отсутствия помех, либо для устранения избыточности сообщения и подготовки с последующему помехоустойчивому кодированию.

4.7 Контрольные вопросы.

• 1. Что такое кодирование?
• 2. Зачем кодируют информацию?
• 3. Назовите основные требования к кодам.
• 4. Что такое оптимальный неравномерный код?
• 5. Назовите основное отличие метода кодирования Хаффмена от метода Шеннона-Фано.

Вау!! 😲 Ты еще не читал? Это зря!

код хаффмана , код шеннона-фано , алгоритм хаффмана ,

Надеюсь, эта статья про кодирование, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое кодирование, декодирование, неравномерные коды и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.