Лекция
Сразу хочу сказать, что здесь никакой воды про энтропия, и только нужная информация. Для того чтобы лучше понимать что такое энтропия, количество информации , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.
В предыдущих  была определена
энтропия как мера неопределенности состояния некоторой физической системы. Очевидно, что в результате получения сведений неопределенность системы может быть уменьшена. Чем больше объем полученных сведений, чем они более содержательны, тем больше будет информация о системе, тем менее неопределенным будет ее состояние. Естественно поэтому
количество информации измерять уменьшением энтропии той системы, для уточнения состояния которой предназначены сведения.
была определена
энтропия как мера неопределенности состояния некоторой физической системы. Очевидно, что в результате получения сведений неопределенность системы может быть уменьшена. Чем больше объем полученных сведений, чем они более содержательны, тем больше будет информация о системе, тем менее неопределенным будет ее состояние. Естественно поэтому
количество информации измерять уменьшением энтропии той системы, для уточнения состояния которой предназначены сведения.
Рассмотрим некоторую систему  , над которой производится наблюдение, и оценим информацию, получаемую в результате того, что состояние системы
, над которой производится наблюдение, и оценим информацию, получаемую в результате того, что состояние системы  становится полностью известным. До получения сведений (априори) энтропия системы была
становится полностью известным. До получения сведений (априори) энтропия системы была 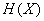 ; после получения сведений состояние системы полностью определилось, т. е. энтропия стала равной нулю. Обозначим
; после получения сведений состояние системы полностью определилось, т. е. энтропия стала равной нулю. Обозначим  информацию, получаемую в результате выяснения состояния системы
информацию, получаемую в результате выяснения состояния системы  . Она равна уменьшению энтропии:
. Она равна уменьшению энтропии:
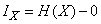
или
 , (18.5.1)
, (18.5.1)
т. е. количество информации, приобретаемое при полном выяснении состояния некоторой физической системы, равно энтропии этой системы.
Представим формулу (18.5.1) в виде:
 , (13.5.2)
, (13.5.2)
где  .
.
Формула (18.5.2) означает, что информация  есть осредненное по всем состояниям системы значение логарифма вероятности состояния с обратным знаком.
есть осредненное по всем состояниям системы значение логарифма вероятности состояния с обратным знаком.
Действительно, для получения  каждое значение
каждое значение  (логарифм вероятности
(логарифм вероятности 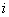 -го состояния) со знаком минус множится на вероятность этого состояния и все такие произведения складываются. Естественно каждое отдельное слагаемое -
-го состояния) со знаком минус множится на вероятность этого состояния и все такие произведения складываются. Естественно каждое отдельное слагаемое -  рассматривать как частную информацию, получаемую от отдельного сообщения, состоящего в том, что система
рассматривать как частную информацию, получаемую от отдельного сообщения, состоящего в том, что система  находится в состоянии
находится в состоянии  . Обозначим эту информацию
. Обозначим эту информацию  :
:
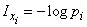 . (18.5.3)
. (18.5.3)
Тогда информация  представится как средняя (или полная) информация, получаемая от всех возможных отдельных сообщений с учетом их вероятностей. Формула (18.5.2) может быть переписана в форме математического ожидания:
представится как средняя (или полная) информация, получаемая от всех возможных отдельных сообщений с учетом их вероятностей. Формула (18.5.2) может быть переписана в форме математического ожидания:
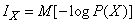 , (18.5.4)
, (18.5.4)
где буквой  обозначено любое (случайное) состояние системы
обозначено любое (случайное) состояние системы  .
.
Так как все числа 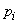 , не больше единицы, то как частная информация так и полная
, не больше единицы, то как частная информация так и полная  не могут быть отрицательными.
не могут быть отрицательными.
Если все возможные состояния системы априори одинаково вероятны  , то, естественно, частная информация
, то, естественно, частная информация  , от каждого отдельного сообщения
, от каждого отдельного сообщения
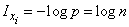
равна средней (полной) информации
 .
.
В случае, когда состояния системы обладают различными вероятностями, информации от разных сообщений неодинаковы: наибольшую информацию несут сообщения о тех событиях, которые априори были наименее вероятны. Например, сообщение о том, что 31 декабря в г. Москве выпал снег, несет гораздо меньше информации, чем аналогичное по содержанию сообщение, что 31 июля в г. Москве выпал снег.
Пример 1. На шахматной доске в одной из клеток произвольным образом поставлена фигура. Априори все положения фигуры на доске одинаково вероятны. Определить информацию, получаемую от сообщения, в какой именно клетке находится фигура.
Решение. Энтропия системы  с
с 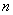 равновероятными состояниями равна
равновероятными состояниями равна  ; в данном случае
; в данном случае
 (дв. ед.),
(дв. ед.),
т. е. сообщение содержит 6 двоичных единиц информации. Так как все состояния системы равновероятны, то ту же информацию несет и любое конкретное сообщение типа: фигура находится в квадрате е2.
Пример 2. В условиях примера 1 определить частную информацию от сообщения, что фигура находится в одной из угловых клеток доски.
Решение. Априорная вероятность состояния, о котором сообщается, равна
 .
.
Частная информация равна
 (дв. ед.).
(дв. ед.).
Пример 3. Определить частную информацию, содержащуюся в сообщении впервые встреченного лица  : «сегодня мой день рождения».
: «сегодня мой день рождения».
Решение. Априори все дни в году с одинаковой вероятностью могут быть днями рождения лица  . Вероятность полученного сообщения
. Вероятность полученного сообщения 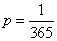 . Частная информация от данного сообщения
. Частная информация от данного сообщения
 (дв. ед.).
(дв. ед.).
Пример 4. В условиях примера 3 определить полную информацию от сообщения, выясняющего, является ли сегодняшний день днем рождения впервые встреченного лица  .
.
Решение. Система, состояние которой выясняется, имеет два возможных состояния:  - день рождения и
- день рождения и 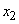 - не день рождения. Вероятности этих состояний
- не день рождения. Вероятности этих состояний  ;
;  .
.
Полная информация равна:
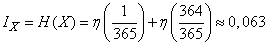 (дв. ед.).
(дв. ед.).
Пример 5. По цели может быть произведено 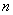 независимых выстрелов; вероятность поражения цели при каждом выстреле равна
независимых выстрелов; вероятность поражения цели при каждом выстреле равна 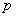 . После
. После 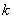 -го выстрела
-го выстрела  производится разведка, сообщающая, поражена или не поражена цель; если она поражена, стрельба по ней прекращается. Определить
производится разведка, сообщающая, поражена или не поражена цель; если она поражена, стрельба по ней прекращается. Определить 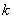 из того условия, чтобы количество информации, доставляемое разведкой, было максимально.
из того условия, чтобы количество информации, доставляемое разведкой, было максимально.
Решение. Рассмотрим физическую систему 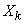 - цель после
- цель после 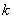 -го выстрела. Возможные состояния системы
-го выстрела. Возможные состояния системы 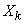 будут
будут
 - цель поражена;
- цель поражена;
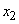 - цель не поражена.
- цель не поражена.
Вероятности состояний даны в таблице:
|
|
|
|
|
|
|
|
Очевидно, информация, доставляемая выяснением состояния системы 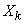 , будет максимальна, когда оба состояния
, будет максимальна, когда оба состояния  и
и 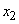 равновероятны:
равновероятны:
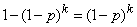 ,
,
откуда
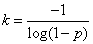 ,
,
где 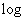 - знак двоичного логарифма.
- знак двоичного логарифма.
Например, при 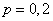 получаем (округляя до ближайшего целого числа)
получаем (округляя до ближайшего целого числа)
 .
.
Если информация выражена в двоичных единицах, то ей можно дать довольно наглядное истолкование, а именно: измеряя информацию в двоичных единицах, мы условно характеризуем ее числом ответов «да» или «нет», с помощью которых можно приобрести ту же информацию. Об этом говорит сайт https://intellect.icu . Действительно, рассмотрим систему с двумя состояниями:
|
|
|
|
|
|
|
|
Чтобы выяснить состояние этой системы, достаточно задать один вопрос, например: находится ли система в состоянии  ? Ответ «да» или «нет» на этот вопрос доставляет некоторую информацию, которая достигает своего максимального значения 1, когда оба состояния априори равновероятны:
? Ответ «да» или «нет» на этот вопрос доставляет некоторую информацию, которая достигает своего максимального значения 1, когда оба состояния априори равновероятны:  . Таким образом, максимальная информация, даваемая ответом «да» или «нет», равна одной двоичной единице.
. Таким образом, максимальная информация, даваемая ответом «да» или «нет», равна одной двоичной единице.
Если информация от какого-то сообщения равна 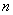 двоичным единицам, то она равносильна информации, даваемой
двоичным единицам, то она равносильна информации, даваемой 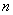 ответами «да» или «нет» на вопросы, поставленные так, что «да» и «нет» одинаково вероятны.
ответами «да» или «нет» на вопросы, поставленные так, что «да» и «нет» одинаково вероятны.
В некоторых простейших случаях для выяснения содержания сообщения действительно удается поставить несколько вопросов так, чтобы ответы «да» и «нет» на эти вопросы были равновероятны. В таких случаях полученная информация фактически измеряется числом таких вопросов.
Если же поставить вопросы точно таким образом не удается, можно утверждать только, что минимальное число вопросов, необходимое для выяснения содержания данного сообщения, не меньше, чем информация, заключенная в сообщении. Чтобы число вопросов было минимальным, нужно формулировать их так, чтобы вероятности ответов «да» и «нет» были как можно ближе к 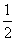 .
.
Пример 6. Некто задумал любое целое число  от единицы до восьми
от единицы до восьми
 ,
,
а нам предлагается угадать его, поставив минимальное число вопросов, на каждый из которых дается ответ «да» или «нет».
Решение. Определяем информацию, заключенную в сообщении, какое число задумано. Априори все значения  от 1 до 8 одинаково вероятны:
от 1 до 8 одинаково вероятны: 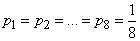 , и формула (18.5.2) дает
, и формула (18.5.2) дает
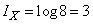 .
.
Минимальное число вопросов, которые нужно поставить для выяснения задуманного числа, не меньше трех.
В данном случае можно, действительно, обойтись тремя вопросами, если сформулировать их так, чтобы вероятности ответов «да» и «нет» были равны.
Пусть, например, задумано число «пять», мы этого не знаем и задаем вопросы:
Вопрос 1. Число  меньше пяти?
меньше пяти?
Ответ. Нет. (Вывод:  - одно из чисел 5, 6, 7, 8.)
- одно из чисел 5, 6, 7, 8.)
Вопрос 2. Число  меньше семи?
меньше семи?
Ответ. Да. (Вывод:  - одно из чисел 5, 6.)
- одно из чисел 5, 6.)
Вопрос 3. Число  меньше шести?
меньше шести?
Ответ. Да. (Вывод: число  равно пяти.)
равно пяти.)
Легко убедиться, что тремя такими (или аналогичными) вопросами можно установить любое задуманное число от 1 до 8.
Таким образом, мы научились измерять информацию о системе  , содержащуюся как в отдельных сообщениях о ее состоянии, так и в самом факте выяснения состояния. При этом предполагалось, что наблюдение ведется непосредственно за самой системой
, содержащуюся как в отдельных сообщениях о ее состоянии, так и в самом факте выяснения состояния. При этом предполагалось, что наблюдение ведется непосредственно за самой системой  . На практике это часто бывает не так: может оказаться, что система
. На практике это часто бывает не так: может оказаться, что система  непосредственно недоступна для наблюдения, и выясняется состояние не самой системы
непосредственно недоступна для наблюдения, и выясняется состояние не самой системы  , а некоторой другой системы
, а некоторой другой системы 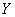 , связанной с нею. Например, вместо непосредственного наблюдения за воздушными целями на посту управления средствами противовоздушной обороны ведется наблюдение за планшетом или экраном отображения воздушной обстановки, на котором цели изображены условными значками. Вместо непосредственного наблюдения за космическим кораблем ведется наблюдение за системой сигналов, передаваемых его аппаратурой. Вместо текста
, связанной с нею. Например, вместо непосредственного наблюдения за воздушными целями на посту управления средствами противовоздушной обороны ведется наблюдение за планшетом или экраном отображения воздушной обстановки, на котором цели изображены условными значками. Вместо непосредственного наблюдения за космическим кораблем ведется наблюдение за системой сигналов, передаваемых его аппаратурой. Вместо текста  отправленной телеграммы получатель наблюдает текст
отправленной телеграммы получатель наблюдает текст 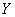 принятой, который не всегда совпадает с
принятой, который не всегда совпадает с  .
.
Различия между непосредственно интересующей нас системой  и поддающейся непосредственному наблюдению
и поддающейся непосредственному наблюдению 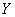 вообще могут быть двух типов:
вообще могут быть двух типов:
1) Различия за счет того, что некоторые состояния системы  не находят отражения в системе
не находят отражения в системе 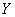 , которая «беднее подробностями», чем система
, которая «беднее подробностями», чем система  .
.
2) Различия за счет ошибок: неточностей измерения параметров системы  и ошибок при передаче сообщений.
и ошибок при передаче сообщений.
Примером различий первого типа могут служить различия, возникающие при округлении численных данных и вообще при грубом описании свойств системы  отображающей ее системой
отображающей ее системой 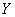 . Примерами различий второго типа могут быть искажения сигналов, возникающие за счет помех (шумов) в каналах связи, за счет неисправностей передающей аппаратуры, за счет рассеянности людей, участвующих в передаче информации, и т. д.
. Примерами различий второго типа могут быть искажения сигналов, возникающие за счет помех (шумов) в каналах связи, за счет неисправностей передающей аппаратуры, за счет рассеянности людей, участвующих в передаче информации, и т. д.
В случае, когда интересующая нас система  и наблюдаемая
и наблюдаемая 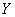 различны, возникает вопрос: какое количество информации о системе
различны, возникает вопрос: какое количество информации о системе  дает наблюдение системы
дает наблюдение системы 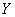 ?
?
Естественно определить эту информацию как уменьшение энтропии системы  в результате получения сведений о состоянии системы
в результате получения сведений о состоянии системы 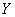 :
:
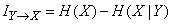 . (18.5.5)
. (18.5.5)
Действительно, до получения сведений о системе 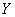 энтропия системы
энтропия системы  была
была 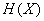 ; после получения сведений «остаточная» энтропия стала
; после получения сведений «остаточная» энтропия стала 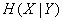 , уничтоженная сведениями энтропия и есть информация
, уничтоженная сведениями энтропия и есть информация 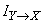 .
.
Величину (18.5.5) мы будем называть полной (или средней) информацией о системе  , содержащейся в системе
, содержащейся в системе 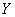 .
.
Докажем, что
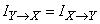 ,
,
т. е. из двух систем каждая содержит относительно другой одну и ту же полную информацию.
Для доказательства запишем энтропию системы 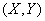 согласно теореме на стр. 479, двумя равносильными формулами:
согласно теореме на стр. 479, двумя равносильными формулами:
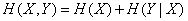 ,
,
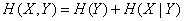 ,
,
откуда
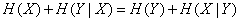 ,
,
 ,
,
или
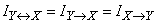 , (18.5.6)
, (18.5.6)
что и требовалось доказать.
Введем обозначение:
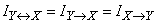 (18.5.7)
(18.5.7)
и будем называть информацию  полной взаимной информацией, содержащейся в системах
полной взаимной информацией, содержащейся в системах  и
и 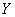 .
.
Посмотрим, во что обращается полная взаимная информация в крайних случаях полной независимости и полной зависимости систем. Если  и
и 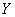 независимы, то
независимы, то 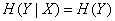 , и
, и
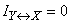 , (18.5.8)
, (18.5.8)
т. е. полная взаимная информация, содержащаяся в независимых системах, равна нулю. Это вполне естественно, так как нельзя получить сведений о системе, наблюдая вместо нее другую, никак с нею не связанную.
Рассмотрим другой крайний случай, когда состояние системы  полностью определяет состояние системы
полностью определяет состояние системы 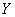 и наоборот (системы эквивалентны). Тогда
и наоборот (системы эквивалентны). Тогда  :
:
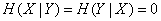
и
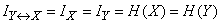 , (18.5.9)
, (18.5.9)
т. е. получается случай, уже рассмотренный нами выше (формула (18.5.2)), когда наблюдается непосредственно интересующая нас система  (или, что то же, эквивалентная ей
(или, что то же, эквивалентная ей 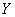 ).
).
Рассмотрим случай, когда между системами  и
и 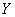 имеется жесткая зависимость, но односторонняя: состояние одной из систем полностью определяет состояние другой, но не наоборот. Условимся называть ту систему, состояние которой полностью определяется состоянием другой, «подчиненной системой». По состоянию подчиненной системы вообще нельзя однозначно определить состояние другой. Например, если система
имеется жесткая зависимость, но односторонняя: состояние одной из систем полностью определяет состояние другой, но не наоборот. Условимся называть ту систему, состояние которой полностью определяется состоянием другой, «подчиненной системой». По состоянию подчиненной системы вообще нельзя однозначно определить состояние другой. Например, если система  представляет собой полный текст сообщения, составленного из ряда букв, a
представляет собой полный текст сообщения, составленного из ряда букв, a 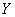 - его сокращенный текст, в котором для сокращения пропущены все гласные буквы, то, читая в сообщении
- его сокращенный текст, в котором для сокращения пропущены все гласные буквы, то, читая в сообщении 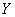 слово «стл», нельзя в точности быть уверенным, означает оно «стол», «стул», «стал» или «устал».
слово «стл», нельзя в точности быть уверенным, означает оно «стол», «стул», «стал» или «устал».
Очевидно, энтропия подчиненной системы меньше, чем энтропия той системы, которой она подчинена.
Определим полную взаимную информацию, содержащуюся в системах, из которых одна является подчиненной.
Пусть из двух систем  и
и 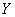 подчиненной является
подчиненной является  . Тогда
. Тогда 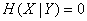 , и
, и
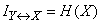 , (18.5.10)
, (18.5.10)
т. е. полная взаимная информация, содержащаяся в системах, из которых одна является подчиненной, равна энтропии подчиненной системы.
Выведем выражение для информации  не через условную энтропию, а непосредственно через энтропию объединенной системы
не через условную энтропию, а непосредственно через энтропию объединенной системы 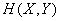 и энтропии ее составных частей
и энтропии ее составных частей 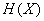 и
и  .
.
Пользуясь теоремой об энтропии объединенной системы (стр. 479), получим:
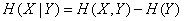 . (18.5.11)
. (18.5.11)
Подставляя это выражение в формулу (18.5.5), получим:
 , (18.5.12)
, (18.5.12)
т. е. полная взаимная информация, содержащаяся в двух системах, равна сумме энтропий составляющих систем минус энтропия объединенной системы.
На основе полученных зависимостей легко вывести общее выражение для полной взаимной информации в виде математического ожидания. Подставляя в (18.5.12) выражения для энтропий:
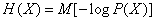 ,
,  ,
,
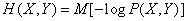 ,
,
получим
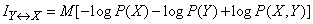
или
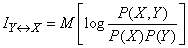 . (18.5.13)
. (18.5.13)
Для непосредственного вычисления полной взаимной информации формулу (18.5.13) удобно записать в виде
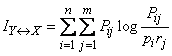 , (18.5.14)
, (18.5.14)
где
 ,
,
 ;
;  .
.
Пример 1. Найти полную взаимную информацию, содержащуюся в системах  и
и 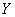 в условиях примера 1
в условиях примера 1 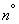 18.4.
18.4.
Решение. Из примера 1  18.4 с помощью таблицы 7 приложения получим:
18.4 с помощью таблицы 7 приложения получим:
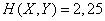 ;
; 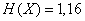 ;
; 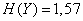 ;
;
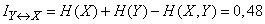 (дв. ед.).
(дв. ед.).
Пример 2. Физическая система  может находиться в одном из четырех состояний
может находиться в одном из четырех состояний 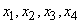 ; соответствующие вероятности даны в таблице
; соответствующие вероятности даны в таблице
|
|
|
|
|
|
|
|
0,1 |
0,2 |
0,4 |
0,3 |
При наблюдении за системой  состояния
состояния 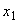 и
и 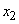 неразличимы; состояния
неразличимы; состояния  и
и  также неразличимы. Сообщение о системе
также неразличимы. Сообщение о системе  указывает, находится ли она в одном из состояний
указывает, находится ли она в одном из состояний 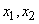 или же в одном из состояний
или же в одном из состояний  . Получено сообщение, указывающее, в каком из состояний:
. Получено сообщение, указывающее, в каком из состояний: 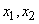 или
или  - находится система
- находится система  . Определить информацию, заключенную в этом сообщении.
. Определить информацию, заключенную в этом сообщении.
Решение. В данном примере мы наблюдаем не саму систему  , а подчиненную ей систему
, а подчиненную ей систему 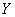 , которая принимает состояние
, которая принимает состояние 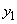 , когда система
, когда система  оказывается в одном из состояний
оказывается в одном из состояний 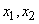 и состояние
и состояние  , когда
, когда  оказывается в одном из состояний
оказывается в одном из состояний  . Имеем:
. Имеем:
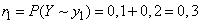 ;
;
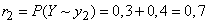 .
.
Находим взаимную информацию, т. е. энтропию подчиненной системы:
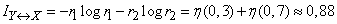 (дв. ед.).
(дв. ед.).
Энтропия и количество информации.
Главным свойством случайных событий является отсутствие полной уверенности в исходе события, что создает неопределенность опытов, реализующих эти события. Степень неопределенности случайных событий различна. Например, опыт с подбрасыванием монеты. Поскольку степень неопределенности исхода того или иного опыта определяется количеством исходов (восход Солнца, игра в шахматы), то очевидно, что функция, измеряющая эту неопределенность, должна зависеть от числа исходов. Сконструируем функцию, для этого сформулируем требования:
1) если количество исходов опыта k=1, то степень неопределенности f(1)=0.
2) чем больше возможных исходов, тем больше степень неопределенности.
Для построения функции рассмотрим сложный опыт:
α — подбрасывание монеты
β — подбрасывание игральной кости.
Благоприятным исходом будем считать одновременное выпадение “герба” и “3”. Потребуем, чтобы к неопределенности первого опыта прибавлялась неопределенность второго опыта. f(αβ)=f(α)+f(β) — этому условно удовлетворяет функция логарифма. Тогда, если опыт имеет k равноверных исходов, то степень неопределенности logak, a=2, f(k)=log2k. f(2)=log22=1 бит — степень неопределенности опыта, имеющих 2 равновесных исхода.
lg10=1 дит; 1 дит=3⅓ бит.
Вероятность: герб — ½, цифра — ½. Рассмотрим какую долю неопределенность вносит в каждый из исходов.
½ log2 2= -½ log2½= - pilog2pi , когда log2 1=1. Если исходы не равновероятные, то H[α]= -∑ki=1 pilog2pi (*). Степень неопределенности опыта α, имеющего k исходов определяется по формуле (*). H — называется энтропией опыта α.
Свойства энтропии:
1) энтропия всегда положительна, H[α]>0
2) при pi à0 или pi à1энтропия стремится к 0, H[α] à0.
3) энтропия достигает максимума, если pi=pj, для любых i,j все исходы равновероятны.
Примеры: 1) имеется 2 урны, в каждой по 20 шаров. В первой урне 10 белых, 5 черных, 5 красных. Во второй урне: 8 белых, 8 черных, 4 красных. Из каждой урны выбирают по шару. Исход каждого из этих опытов следует считать более неопределенно.
1) вероятность: белых - ½, черных — 1/4, красных — 1/4.
2) вероятность: белых — 2/5, черных — 2/5, красных — 1/5.
H[α1]= -½ log2½ - 1/4log21/4 - 1/4log21/4 =½+½+½=1,5 бит.
H[α2]= -2/5 log22/5 — 2/5log22/5 - 1/5log21/5 =1,52 бит.
Ответ: исход второго опыта следует считать более неопределенным на 0,02 бит.
Энтропия определена как мера неопределенности состояния некоторых систем. Очевидно, что в результате получения сообщения знание о состоянии системы увеличивается, при этом степень неопределенности системы уменьшается. Если сообщение несет полную информацию о состоянии системы, то неопределенность становится равной 0. Таким образом величину получаемой информации можно оценить изменением энтропии. Отсюда количество информации об опыте α можно оценить как J[α]=H[α]-Hε[α] (1).
H[α] — начальная энтропия, Hε[α] — остаточная энтропия.
Если получена полная информация об объекте, то J[α]=H[α] (2).
В частном случае, когда pi=pj, для любых i,j, то J[α]= -∑ki=1pilogpi= -k*1/k*log21/k=log2k, т.е. при равновесном исходе J[α]=log2k.
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про энтропия Надеюсь, что теперь ты понял что такое энтропия, количество информации и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Теория информации и кодирования
Термины: Теория информации и кодирования