Лекция
Привет, сегодня поговорим про кодирование источника дискретных сообщений в канале с помехами, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое кодирование источника дискретных сообщений в канале с помехами, принципы помехоустойчивого кодирования , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.
Лекция 5.
 5.1 Кодирование информации для канала с помехами. Теорема Шеннона для канала с помехами.
5.1 Кодирование информации для канала с помехами. Теорема Шеннона для канала с помехами.На этой лекции мы приступим к изучению помехоустойчивого кодирования. Оно предназначено для обнаружения и исправления ошибок символов в кодовых словах, возникающих в канале передачи при воздействии помех и шумов.
Рассмотрим вначале, какие ошибки возникают чаще всего а какие реже.
Для этого рассмотримпростейшую модель канала с помехами. Это Двоичный СимМетричный Канал (ДСМК). Симметричность канала означает, что вероятность ошибки, для 0 и для 1 одинакова и равна p.
При передаче информации через ДСМК помеха способна с некоторой вероятностью p превратить 0 в 1 или 1 в 0. Передачу информации через ДСМК можно представить в виде следующего графа, изображенного на рис. 5.1:
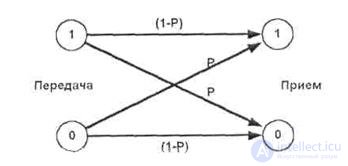
Рис.5.1
Расчет вероятности искажения кодового слова в ДСМК
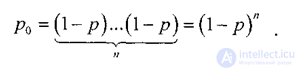
Преположим, кодовое слово состоит из nдвоичных символов. Вероятность неискажения всего кодового слова, как несложно доказать, равна:
Вероятность искажения одного символа (однократная ошибка):
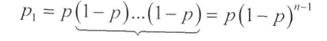
А для одновременного искажения нескольких символов (кратная ошибка)
Pr=pr*(1-p)(n-r)
При вероятности ошибки p<0.5, (то есть канал не слишком плохой) из этого выражения следует, что с ростом кратности ошибки (r) ее вероятность быстро уменьшается. Таким образом малократные ошибки (1, 2, 3 символа) гораздо более вероятны, чем многократные. С ними и следует бороться в первую очередь.
 Кодирование информации для канала с помехами. Теорема Шеннона для канала с помехами.
Кодирование информации для канала с помехами. Теорема Шеннона для канала с помехами.
Ошибка в кодовой комбинации появляется при ее передаче по каналу связи вследствие замены одних элементов другими под воздействием помех.Например, 2-кратная ошибка возникает при замене (искажении) двух элементов. Например, если кодовая комбинация 01101 принята как 01011 то имеет место двукратная ошибка.
Напомнимкратко основные характеристики канала связи. Пропускная способность канала связи определяется как максимальное количество информации, которое канал может пропустить за единицу времени. Скорость передач это количество информации , которое канал реально пропускает за единицу времени. То есть пропускная способность - это максимальная скорость передачи.
Производительность источника - это количество информации, вырабатываемое источником за единицу времени.
Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Шенноном и сформулирована в виде теоремы из двух частей.
1.При любой производительности источника сообщений, меньшей, чем пропускная способность канала, существует такой способ кодирования, который позволяет обеспечить передачу всей информации, создаваемой источником сообщений, со сколь угодно малой вероятностью ошибки.
2. Об этом говорит сайт https://intellect.icu . Не существует способа кодирования, позволяющего вести передачу информации со сколь угодно малой вероятностью ошибки, если производительность источника сообщений больше пропускной способности канала.
Из теоремы Шеннонаследует, что помехи в канале не накладывают ограничений на точность передачи. Ограничение накладывается только на скорость передачи, при которой может быть достигнута сколь угодно высокая точность передачи. То есть даже при больших помехах в канале можно точно, но медленно передавать информацию.
Теорема не дает нам метода или способа построения кодов, обеспечивающих безошибочную передачу информации при воздействии помех , но обосновывает принципиальную возможность такого кодирования, что позволяет с оптимизмом вести разработку конкретных помехоустойчивых кодов.
При любой конечной скорости передачи информации вплоть до пропускной способности канала, сколь угодно малая вероятность ошибки достигается лишь при безграничном увеличении длительности кодируемых последовательностей знаков. Таким образом, безошибочная передача при наличии помех возможна лишь теоретически.
Обеспечение передачи информации с весьма малой вероятностью ошибки и достаточно высокой эффективностью возможно лишь при кодировании чрезвычайно длинными последовательностями знаков.
На практике точность передачи информации и эффективность каналов связи ограничивается двумя факторами:
Коды, которые обеспечивают возможность обнаружения и исправления ошибки, называют помехоустойчивыми. Эти коды используют для:
Корректирующие коды и коды для обнаружения ошибок основаны на введении избыточности.
Помехоустойчивые коды подразделяются на два класса:
В случае блоковых кодов процедура кодирования заключается в преобразованииили кодировании последовательности информационных символов входного кодового слова впомехоустойчивое кодовое слово но уже большей длины. Большая длина помехоустойчивого кода обусловлена введением при кодировании дополнительных или корректирующих символов, которые и обеспечивают обнаружение и исправление ошибок.
В операциях по кодированию принимают участие только информационные символы входного слова и выходная последовательность помехоустойчивого кодового слова зависит только от них.
Блоковыйкодназывают равномерным,если его длина n остаетсяпостояннымдлявсех информационных кодовых слов длиной k символов,
Различают систематические и несистематические блоковые коды. При кодировании систематическими кодами выходные последовательности состоят из символов, роль которых может быть отчетливо разграничена. Это информационные символы, совпадающие с символами последовательности, поступающей на вход кодера канала, и избыточные (проверочные) символы, вводимые в исходную последовательность кодером канала и служащие для обнаружения и исправления ошибок.
При кодировании несистематическими кодами разделить символы входной последовательности на информационные и проверочные невозможно.
Непрерывными-называют такие коды, в которых введение избыточных символов в кодируемую последовательность информационных символов осуществляется непрерывно, без разделения ее на независимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми. Мы их рассматривать не будем.
Способность кода обнаруживать и исправлять ошибки обусловлена наличием в нем избыточных символов.
Приведенный ниже рисунок иллюстрирует принципы построения помехоустойчивых кодов.
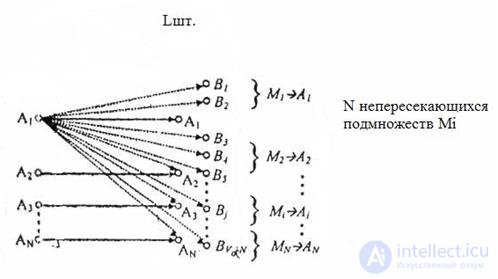
Рис.5.1
Рисунок иллюстрирует процесс помехоустойчивого кодирования путем увеличения числа выходных кодовых последовательностей, связанных с исходными информационными кодовыми словами.
На вход кодирующего устройства поступает последовательность из k информационных двоичных символов. На выходе ей соответствует последовательность из n двоичных символов, причем n>k.
Всего может быть N=2k различных входных и L=2n различных выходных последовательностей.
Из общегочисла 2n, выходныхпоследовательностейтолько N=2k. последовательностей соответствуют входным. Их называют разрешенными кодовыми комбинациями.
Остальные L-Nвозможныхвыходныхпоследовательностейдляпередачине используются. Их называют запрещенными кодовыми комбинациями.
Искажения информации в процессе передачи сводятся к тому, что некоторые из передаваемых символов заменяются другими - неверными.
Так как каждая из N=2k разрешенных комбинаций в результате действия помех может трансформироваться в любую другую, то всегда имеется L*N возможных случаев передачи. В это число входят:
1) N=2k случаев безошибочной передачи;
2) N*(N-1)= 2k(2k -1) случаев перехода в другие разрешенные комбинации, что соответствует необнаруженным ошибкам;
3) N*(L-N)=2k(2n - 2k) случаев перехода в неразрешенные комбинации, которые могут быть обнаружены.
Следовательно, часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи составляет
N(L-N)/(N*L)=(L-N)/L=1-N/L.
Пример: Определить обнаруживающую способность кода, каждая комбинация которого содержит всего один избыточный символ (n=k+l).
Решение : 1. Общее число выходных последовательностей составляет 2(k+1) , т.е. вдвое больше общего числа кодируемых входных последовательностей.
2. За подмножество разрешенных кодовых комбинаций можно принять, например, подмножество комбинаций, содержащих четное число единиц (или нулей).
3. При кодировании к каждой последовательности из k информационных символов добавляют один символ (0 или 1), такой, чтобы число единиц в кодовой комбинации было четным. Получение слова с нечетным числом единиц переводит разрешенную кодовую комбинацию в подмножество запрещенных комбинаций, что обнаруживается на приемной стороне по нечетности числа единиц. Часть опознанных ошибок составляет
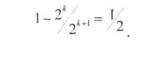
или 0.5 от общего числа возможных кодовых комбинаций.
Любой метод декодирования можно рассматривать как правило разбиения всего множества запрещенных кодовых комбинаций на N=2k непересекающихся подмножеств Mj, каждое из которых ставится в соответствие одной из разрешенных комбинаций. При получении разращенной комбинации,принадлежащей подмножеству Мj,принимают решение, что передавалась разрешенная комбинация Аj;.Ошибка будет исправлена в тех случаях, когда полученная комбинация действительно образовалась из Аj, т.е. L-N случаях.
Всего случаев перехода в неразрешенные комбинации
L(L-N)=2k (2n - 2k ).
Таким образом, при наличии избыточности любой код способен исправлять ошибки.
Отношение числа исправляемых кодом ошибочных кодовых комбинаций к числу обнаруживаемых ошибочных комбинаций равно
(L-N)/N(L-N)=1/N=2k.
Способ разбиения на подмножества зависит от того, какие ошибки должны исправляться конкретным кодом.
Большинство разработанных кодов предназначено для корректирования взаимно независимых ошибок определенной кратности и пачек (или пакетов) ошибок.
Взаимно независимыми ошибкаминазывают такиеискажениявпередаваемом кодовом слове символов, при которых вероятность появления любой комбинации искаженных символов зависит только от числа искаженных символови вероятности искажения одиночного символа p .
При взаимнонезависимых ошибках вероятностьискажения любых г символов в n- разрядной кодовой комбинации, как уже указывалось для модели двоичного симметричного канала:
Pr=pr*(1-p)(n-r)
где р - вероятность искажения одного символа; r - число искаженных символов; n- число двоичных символов кодового слова.
Если учесть, что р<<1, то в этом случае наиболее вероятны ошибки низшей кратности. Их следует обнаруживать и исправлять в первую очередь.
При взаимно независимых ошибках наиболее вероятен переход в кодовую комбинацию, отличающуюся от данной в наименьшем числе символов.
Степень отличия любых двух кодовых комбинаций характеризуется расстоянием между ними в смысле Хэмминга или просто кодовым расстоянием.
Кодовое расстояние выражается числом символов, в которых комбинации отличаются одна от другой, и обозначается через d.
Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2. Например

Минимальное расстояние, взятое по всем парам кодовых разрешенных комбинаций кода, называют минимальным кодовым расстоянием.
Более полное представление о свойствах кода дает матрица расстоянийD, элементы которой dij (i,j = 1,2,...,n) равны расстояниям между каждой парой из всех m разрешенных комбинаций.
Пример: Представить симметричной матрицей расстояний код X1 = 000; Х2 = 001; Х3 = 010;X4=111
Решение. . Минимальное кодовое расстояние для кода d=1.
Это вытекает из рассмотрениясимметричная матрицы всех возможных кодовых расстояний между словами кода.
Таблица 5.1
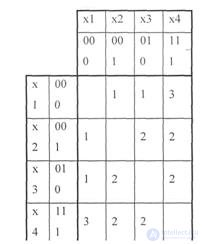
Декодирование после приема производится таким образом, что принятая кодовая комбинация отождествляется с той разрешенной, которая находится от нее на наименьшем кодовом расстоянии.
Такое декодирование называетсядекодированием по методумаксимального правдоподобия.
Надеюсь, эта статья про кодирование источника дискретных сообщений в канале с помехами, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое кодирование источника дискретных сообщений в канале с помехами, принципы помехоустойчивого кодирования и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Теория информации и кодирования
Термины: Теория информации и кодирования