Основные виды энтропииди скретных источников. Условная и взаимная энтропии

Привет, сегодня поговорим про основные виды энтропииди скретных источников условная, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое основные виды энтропииди скретных источников условная, взаимная энтропии , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

Тема2. Основные виды энтропииди скретных источников. Условная и взаимная энтропии .

Лекция2.

2.1Условнаяэнтропия.

Для дальнейшего изложения нам понадобятся некоторые известные сведения из теории вероятности.

1) Свойства вероятностей для ансамбля случайных событий А и В:

P(A,B)=P(A)*P(B/A); -> P(B/A)=P(A,B)/P(B);

P(A,B)=P(B)*P(B/A); -> P(A/B)=P(A,B)/P(A);

P(A/B)=P(A)*P(B/A)/P(B);P(B/A)=P(B)*P(A/B)/P(A);

Если А и В независимы, то

P(A/B)=P(A); P(B/A)=P(B):

P(A,B)=P(A)*P(B);

Еще раз определение энтропии по Шеннону для источника дискретных сообщений:

_{<![if !vml]>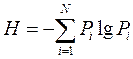<![endif]>}

Еесвойства:

Н > 0 ;

Нmах = log N;

При независимых источниках H(A,B)=H(A)+H(B);

 

УСЛОВНАЯ ЭНТРОПИЯ

Если состояния элементов системы не зависят друг от друга илиесли состояние одной системы не зависит от состояния другой системы, то неопределенность того, что некоторый элемент системы (или некоторая система) будет находиться в одном из возможных состояний, полностью определялась бы вероятностными характеристиками отдельных элементов системы. В этом случае удельное количество информации на состояние элемента системы или на один символ сообщений называется средней энтропией, а при ее вычислении используется выражение

_{<![if !vml]>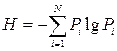<![endif]>}

При подсчете среднего количества информации на символ сообщения взаимозависимость учитывают через условные вероятности наступления одних событий относительно других, а полученную при этом энтропиюназывают условной энтропией.

Рассмотрим передачу сообщений источника случайных символов А через канал передачи информации. При это полагается, что при достоверной передаче при передаче символа a₁ получаем b₁, a₂ - b₂ и т.д. При этом для канала с помехами передача искажается, и при получении символа b₁ можно лишь говорить о вероятности передачи символа a₁. Вполне может быть, что были переданы символы a₂, a₃ и т.д.

Искажения описываются матрицей условных вероятностей канала P(A/B)={p(a_i/b_i}, как єто изображено на рис. 2.1

 

<![if !vml]><![endif]>

Рис. 2.1

Рассмотрим процесс передачи сигналов по каналу связи с помехами и используем его для уяснения механизма вычисления условной энтропии.

Если источник сообщений выдает символы

a_l, а₂, ..., a_i ..., а_n

с вероятностями соответственно

р (а₁), р (а₂) ... ..., р (а_i), ..., р (а_n),

а на выходе канала передачи мы получаем символы

b₁ ,b₂, ..., b_i ..., b_n

с вероятностями соответственно

р (b₁), р (b₂), ..., р (b_i, ..., р (b_n),

то понятие условной энтропии Н (B/a_i) выражает неопределенность того, что, отправив a_i, мы получим b_i., понятие H(A/b_i) неуверенность, которая остается после получения b_i в том, что было отправлено именно a_i. Графически это представлено на вышеприведенном рисунке. Если в канале связи присутствуют помехи, то с различной степенью вероятности может быть принят любой из сигналов b_j и, наоборот, принятый сигнал b_j может появиться и результате отправления любого из сигналов a_i. Если в канале связи помехи отсутствуют, то всегда посланному символу а₁ соответствует принятый символ b₁,а₂— b₂, ..., а_n— b_n.

При этом энтропия источника сообщений H(А) равна энтропии приемника сообщений Н (В). Если в канале связи присутствуютпомехи, то они уничтожают или искажают часть передаваемой информации.

Информационные потери полностью описываются через частную и общую условную энтропию. Вычисление частных и общей условной энтропии удобно производить при помощи канальных матриц. Термин «канальная матрица», означающий: матрица, статистически описывающая данный канал связи, применяется для краткости. Если канал связи описывается со стороны источника сообщений (т. е. известен посланный сигнал), то вероятность того, что при передаче сигнала a_i по каналу связи с помехами мы получим сигнал b_j обозначается как условная вероятность р (b_j/a_i). а канальная матрица имеет вид

<![if !vml]>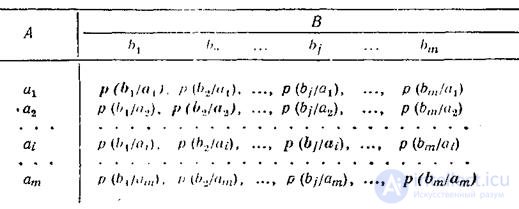<![endif]>

Вероятности, которые расположены по диагонали (выделенные полужирным шрифтом), определяют вероятности правильного приема, остальные — ложного. Значения цифр, заполняющих колонки канальной матрицы, обычно уменьшаются по мере удаления от главной диагонали и при полном отсутствии помех все, кроме цифр, расположенных на главной диагонали, равны нулю.

Прохождение символа a_i со стороны источника сообщений в данном канале связи описывается распределением условных вероятностей вида р(b_j/a_i), сумма вероятностей которого всегда должна быть равна единице. Например, для сигналаа₁

 

<![if !vml]>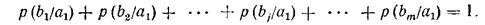<![endif]>

 

Потери информации, приходящиеся на долю сигнала a_i описываются при помощи частной условной энтропии. Например, для сигналаa₁

<![if !vml]>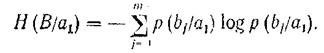<![endif]>

Суммирование производится по j, так как i-е состояние (в данном случае первое) остаетсяпостоянным.

Потери при передаче всех сигналов по данному каналу связи описываются при помощи общей условной энтропии. Дли ее вычисления следует просуммировать все частные условные энтропии, т. е. произвести двойное суммирование по i и по j.

В случае неравновероятногопоявлениясимволовисточника сообщений следует учесть вероятность появления каждого символа, умноживнанее соответствующую частную условную энтропию. Об этом говорит сайт https://intellect.icu . Приэтом общаяусловнаяэнтропия

<![if !vml]>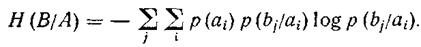<![endif]>

Если исследовать ситуацию со стороны приемника сообщений (то есть когда известен принятый сигнал) , то с получением символа b_j предполагается, что был послан какой-то из символов a₁, a₂, …, a_i,…,a_m. В этом случае канальная матрица имеет вид:

 

<![if !vml]>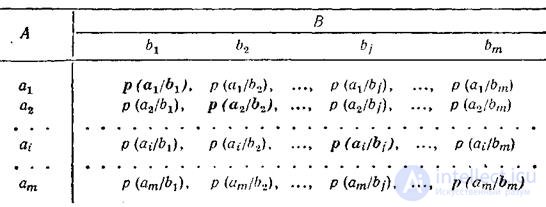<![endif]>

В этом случае единице должны равняться суммы условныхвероятностей не по строкам, а по столбцам канальной матрицы

<![if !vml]>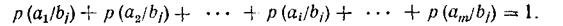<![endif]>

 

Частная условная энтропия

 

<![if !vml]>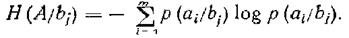<![endif]>

А общая условная энтропия

 

<![if !vml]>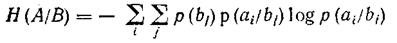<![endif]>

Общая условная энтропия системы В относительно системы А характеризует количество информации, содержащейся в любом символе источника сообщений, через который мы представляем состояния элементов исследуемых систем.

Общую условную энтропию определяют путем усреднения по всем символам, т. е. по всем состояниям а_i с учетом вероятности появления каждого из них. Она равна сумме произведений вероятностей появления символов источника на неопределенность, которая остается после того, как адресат принял символы:

<![if !vml]>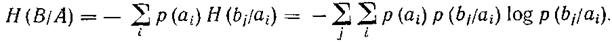<![endif]>

Если в канале связи помехи отсутствуют, то все элементы канальной матрицы, кроме расположенных на главной диагонали, равны нулю. Это говорит о том, что при передаче сигнала а₁ мы наверняка получим b₁ при передаче а₂ -b₂, ..., а_m— b_m. Вероятность получения правильного сигнала станет безусловной, а условная энтропия будет равна нулю.

Своего максимумаусловная энтропия достигает в случае,когда при передаче символа а_i может быть с равной вероятностью полученлюбой из сигналовb₁, b₂, ..., b_m.

 

2.2Основныесвойстваусловнойэнтропии.

Свойство 1. Если ансамбли сообщений А и В взаимонезависимы, то условная энтропия А относительно В равна безусловной энтропии А,и наоборот условная энтропия В относительно А равна безусловной энтропии В

<![if !vml]>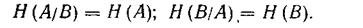<![endif]>

Доказательство. Если сообщения А и В взаимонезависимы, то условные вероятности отдельных символов равны безусловным:

<![if !vml]><![endif]>

Так какр (а_i)* р (b_j/a_i) = p (a_i, b_j), то выражение для H(B/A)представим в виде:

<![if !vml]>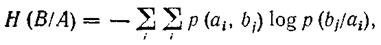<![endif]>

подставив в полученное выражение ,

<![if !vml]><![endif]>

получим

<![if !vml]>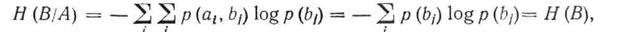<![endif]>

так как

<![if !vml]>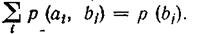<![endif]>

Свойство 2: Если ансамбли сообщений А и В настолько жестко статистически связаны, что появление одного из них непременно подразумевает появление другого, то их условные энтропии равны нулю:

<![if !vml]>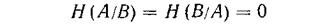<![endif]>

Доказательство.Воспользуемся свойствамивероятностей,согласно которым при полной статистическойзависимости р(b_j/a_i) = 1, слагаемые р (b_j/a_i)*log(р (b_j/a_i)в выражении для энтропии также равны нулю. Если нулю равны отдельные слагаемые, то и сумма равна нулю, откуда

<![if !vml]>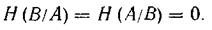<![endif]>

Выводы:

1. Энтропия сообщения, составленного с учетом неравновероятности символов меньше, чем энтропия сообщения, составленного из равновероятных символов.

2. Энтропия сообщения, составленного с учетом взаимозависимости символов, меньше, чем энтропия того же сообщения, составленного из независимых символов.

3. Максимальную энтропию имеют сообщения, составленные из равновероятных и независимых символов, т. е. те, у которых условная энтропияравнанулю, а вероятностьпоявления символов алфавита p_i=1/N.

2.3 Взаимная энтропия. Свойства энтропии объединения.

Энтропия объединения или взаимная энтропия используется для вычисления энтропии совместного появления статистически зависимых сообщений либо энтропии взаимосвязанных систем.

Например, при передаче по каналу связи с шумами цифры 5, из 100 раз цифра 5 была принята 90 раз, цифра 6 — восемь раз,цифра 4 — два раза. Неопределенность возникновения комбинаций вида 5—4; 5—5; 5—6 припередаче цифры 5 может быть описана при помощи энтропии объединенияН (А, В).

Понимание энтропии объединения (иногда употребляют термин «взаимная энтропия») облегчается, если рассуждения сводятся к некоторому условному каналу связи. На примере передачи информации по каналу связи также удобнее проследить взаимосвязь понятий условной энтропии Н (В/А) и взаимной энтропии H(А, В).

Итак, пусть (а₁, а₂, ..., а_i .... а_n) есть выборочное пространство А, или символы характеризующееисточниксообщений,a(b_1, b₂, …, b_j,…,b_m)выборочное пространство В, или символы, характеризующее приемник сообщений. При этом а есть сигнал на входе шумящего капала, а b - сигнал на его выходе. Взаимосвязь переданных и принятых сигналов описывается вероятностями совместных событий вида p(a,b), а взаимосвязь выборочных пространств А и В описывается матрицей вида:

<![if !vml]>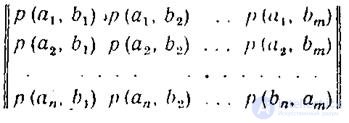<![endif]>

 

Если матрица описывает канал связи, то число строк матрицы равно числу столбцов m=nи пределы суммирования по i и по j одинаковы. При описании взаимодействия систем равенство m=n необязательно.

Независимо от равенства или неравенства числа строк числу столбцов матрица объединенияобладает свойством:

<![if !vml]>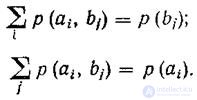<![endif]>

В свою очередь,

<![if !vml]>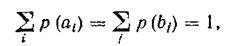<![endif]>

т. е.

<![if !vml]><![endif]>

Это свойство позволяет вычислять энтропию источника и приемника сообщений непосредственно по матрице объединения :

<![if !vml]>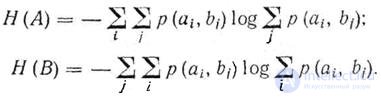<![endif]>

До знака логарифма суммирование производится по i и j, так как для нахождения безусловных вероятностей необходимо производить суммирование по одной координате (имеется в виду матричное представление вероятностей), а для нахождения соответствующей энтропии суммирование производится по другой координате.

Условные вероятности 'при помощи матрицы объединения находятся следующим образом:

<![if !vml]>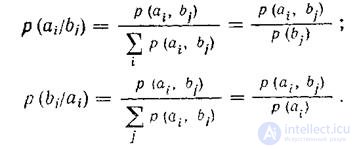<![endif]>

<![if !vml]>

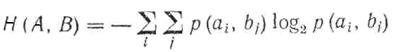<![endif]>
Энтропия объединения ансамблей А и В при помощи матрицы объединения вычисляется путем последовательного суммирования по строкам или gо столбцам всех вероятностей вида р(а, b), умноженных на логарифм этих же вероятностей

Размерность этой энтропии- «бит/два символа»

Размерность «бит/два символа» объясняетсятем,чтовзаимная энтропиипредставляет собой неопределенность возникновения пары символов, т.е. неопределенность на два символа. В случае отсутствия зависимости междусимволами выражение для H(A,B) принимает вид выражения H(A) или H(B) , и соответственно размерность будет«бит/символ».

Исследуемвыражениедля взаимной энтропии

Из теориивероятностей известно, что (смотрим на основные соотношения в начале лекции)

<![if !vml]>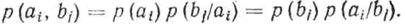<![endif]>

Используя это свойство, выражение для взаимной энтропии можно записать как

<![if !vml]>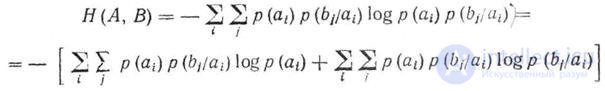<![endif]>

 

Но

<![if !vml]>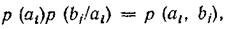<![endif]>

и ,

<![if !vml]>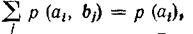<![endif]>

тогда первое слагаемое выражение принимает вид

 

<![if !vml]>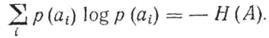<![endif]>

 

Второе слагаемое, есть не что иное,как H(В/А), что позволяет выражениезаписать в виде

 

<![if !vml]>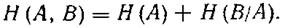<![endif]>

 

Энтропия объединения передаваемого ансамбля А и принимаемого ансамбля В равна сумме безусловной энтропииH(A) и условной энтропии Н (В/А).

Последняя в данном случае представляет ту добавочную информацию, которую дает сообщениеВ после того, как стала известна информация, содержащаяся в сообщении А. Таким образом, условная энтропия представляет собой неопределенность того, что при приеме b было послано а, а взаимная энтропия отражает неопределенность возникновения пары вида ab.

Энтропия объединения обладает свойством симметрии.

H(A,B)=H(B,A)

Свойство симметрии энтропии объединения хорошо иллюстрируется матрицей, изображенной на рисунке 2.2

<![if !vml]>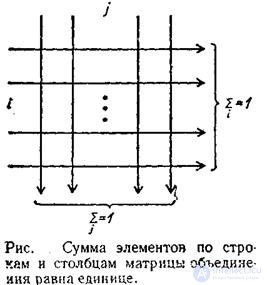<![endif]>

Рис. 2.2

Действительно, если просуммировать все элементы матрицы объединения по строкам и но столбцам по схеме рисунка а затем сложить полученные результаты, то обе суммы будут равны единице. Свойство симметрии позволяет записать соотношения между условной энтропией и энтропией объединения следующим образом:

<![if !vml]><![endif]>

Если построена матрица вероятностей р(a,b), описывающая взаимосвязь двух произвольных выборочных пространств, в частности взаимосвязь входа и выхода шумящего канала связи, то остальные информационные характеристики могут не задаваться, так как матрица взаимной энтропии обладает информационной полнотой.

Взаимная информациямежду ансамблем сообщений источника А и приемника В выражается формулами

 

<![if !vml]>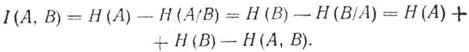<![endif]>

<![if !vml]>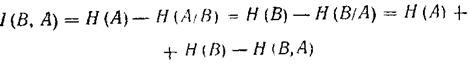<![endif]>

При отсутствиистатистическойзависимостимеждуэлементами ансамблей А и В условные вероятности превращаются в безусловные

<![if !vml]>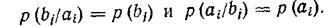<![endif]>

В этом случае

<![if !vml]><![endif]>

 

При полной статистической зависимости между элементами ансамблей А и В (например, когда результат одного события однозначно определяет информацию о другом событии)

Н(В/А) = Н (А/В) = 0,

а взаимнаяэнтропия

<![if !vml]>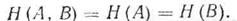<![endif]>

В случае передачи информации по каналам связи полная статистическая зависимость между передаваемыми и принимаемыми сигналами говорит об отсутствии помех,канальнаяматрицаприобретаетвид

<![if !vml]>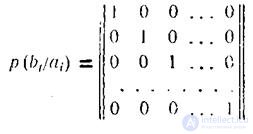<![endif]>

условные вероятности правильного приема равны единице, остальные - нулю, что превращает в нуль все частные условные энтропии.

<![if !vml]>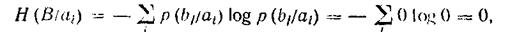<![endif]>

аналогично

<![if !vml]>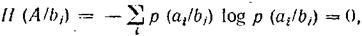<![endif]>

и, следовательно, и общая условная энтропия превращается в нуль и выражение для Н(А,В) приобретает вид

<![if !vml]>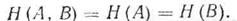<![endif]>

 

Выводы:

1.Энтропия объединенной системы А, В равна безусловной энтропии одной из них плюс условная энтропия второй относительно первой.

2. Матрица «объединения», описывающая взаимодействие систем или ансамблей сообщений при помощи вероятностей совместных событии,обладает свойствоминформационнойполноты( а сумма ее элементовравна 1).

3. Взаимная энтропия ансамблей произвольных выборочных пространств обладает свойством взаимной симметрии.

4. В случае статистической независимости элементов ансамблей взаимная энтропия любого количества ансамблей ровна сумме их безусловных энтропий.

5. При полной статистической зависимости ансамбля источника сообщений и ансамбля приемника сообщений их взаимная энтропия равна безусловной энтропииисточника сообщений.

 

2.4 Контрольные вопросы.

1. Каков основной смысл понятия условной энтропии.

2. Дайте понятие канальной матрицы канала с помехами.

3. Перечислите основные свойства условной энтропии.

4. Назовите основной взаимной энтропии.

5. Что более полно определяет канал передачи информации: условная или взаимная энтропия?

Надеюсь, эта статья про основные виды энтропииди скретных источников условная, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое основные виды энтропииди скретных источников условная, взаимная энтропии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.