Лекция
Привет, сегодня поговорим про предмет теории информации, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое предмет теории информации, количественная мера информации, свойства энтропии , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.
Теория информации является одним из курсов при подготовке специалистов информационных систем, автоматизированных систем управления и обработки информации.Функционирование таких систем существенносвязаносполучением,подготовкой,передачей,хранением и обработкой информации, поскольку без осуществления этих этапов невозможно принятьправильноерешениеиосуществитьтребуемоеуправляющее воздействие, которое является конечной целью функционирования любой системы.
Возникновение теории информации связывают обычно с появлением фундаментальной работы американского ученого К. Шеннона «Математическая теория связи» (1948).Однако в теорию информации органически вошли и результаты, полученныедругимиучеными.Например,Р. Хартли, впервые предложил количественную меру информации (1928), советский академик В. А. Котельников, сформулировал важнейшую теорему о возможности представления непрерывной функции совокупностью ее значений в отдельных точках отсчета (1933) и разработал оптимальные методы приема сигналов на фоне помех.
К теории информации, в ее классической постановке,относят следующие вопросы:
Если рассматривают проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации.
Попытки широкого использования идей теории информации в различных областях науки связаны с тем, что в основе своей эта теория математическая. Основные ее понятия (энтропия, количество информации, пропускная способность) определяются только через вероятности событий, которым может быть приписано самое различное физическое содержание. Подход к исследованиям в других областях науки с позиций использования основных идей теории информации получил название теоретико-информационного подхода. Его применение в ряде случаев позволило получить новые теоретические результаты и ценные практические рекомендации. Однако нередко такой подход приводит к созданию моделей процессов, далеко не адекватных реальной действительности. Поэтому в любых исследованиях, выходящих за рамки чисто технических проблем передачи и хранения сообщений, теорией информации следует пользоваться с большой осторожностью. Особенно это касается моделирования умственной деятельности человека, процессов восприятия, оценки и обработки им информации.
Содержание конспекта лекций ограничивается рассмотрением вопросов теории и практики кодирования в ее узком техническом смысле.
Что такое информация? С начала 1950-х годов предпринимаются попытки использовать понятие информации (не имеющее до настоящего времени единого определения) для объяснения и описания самых разнообразных явлений и процессов.
В некоторых учебниках дается следующее определение информации:
Информация - это совокупность сведений, подлежащих хранению, передаче, обработке.
Такое определение помогает хотя бы смутно представить, о чем идет речь. Но с точки зрения логики оно бессмысленно. Определяемое понятие (информация) здесь подменяется другим понятием (совокупность сведений), которое само нуждается в определении.
При всех различиях в трактовке понятия информации, бесспорно, то, что проявляется информация всегда в материально-энергетической форме в виде сигналов при передаче, приеме и хранении данных.
Можно выделить следующие этапы обращения информации:
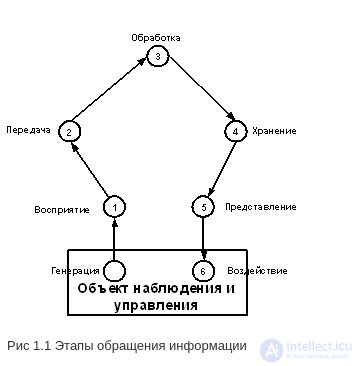
Рис 1.1 Этапы обращения информации
На этапе обработки информации осуществляется целенаправленное извлечение и анализ информации о каком-либо объекте (процессе), в результате чего формируется образ объекта, проводится его опознание и оценка. При этом отделяют интересующую информацию от шумов и помех.
На этапе подготовки информации получают сигнал в форме, удобной для передачи или обработки (нормализация, аналого-цифровое преобразование и т.д.).
На этапе передачи и хранения информация пересылается либо из одного места в другое, либо от одного момента времени до другого (хранение информации)
На этапе обработки информации выделяются ее общие и существенные взаимозависимости для выбора управляющих воздействий (принятия решений).
На этапе отображения информации она представляется человеку в форме, способной воздействовать на его органы чувств.
На этапе воздействия информация используется для осуществления необходимых изменений в системе.
Информация поступает в систему в форме сообщений. Под сообщением понимают совокупность знаков или первичных сигналов, содержащих информацию.
Источник сообщении в общем случае образует совокупность источника информации (ИИ) (исследуемого или наблюдаемого объекта) и первичного преобразователя (ПП) (датчика, человека-оператора и т.д.), воспринимающего информацию о протекающем в нем процессе.
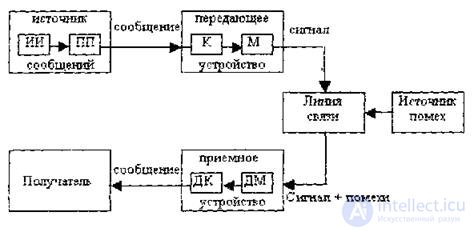 <
<
Рис. 1.2 Структурная схема одноканальной системы передачи информации.
Различают дискретные и непрерывные сообщения.
Дискретные сообщения формируются в результате последовательной выдачи источником сообщений отдельных элементов - знаков или символов.
Множестворазличныхсимволовназываюталфавитомисточника сообщения, а число символов - объемом алфавита.
Непрерывные сообщения не разделены на элементы. Они описываются непрерывными функциями времени, принимающими непрерывное множество значений (речь, телевизионное изображение). Мы будем рассматривать лишь некоторые аспекты информационных характеристик источников непрерывных сообщений для определения потенциала источников сообщений и каналов передач.
Преобразование сообщения в сигнал, удобный для передачи по данному каналу связи, называют кодированием в 'широком смысле слова.
Операцию восстановления сообщения по принятому сигналу называют декодированием.
При кодировании дискретного источника, как правило, прибегают к операции представления исходных знаков в другом алфавите с меньшим числом знаков, называемых символами. При обозначении этой операции используется тот же термин "кодирование", рассматриваемый в узком смысле. Устройство, выполняющее такую операцию, называют кодирующим или кодером. Так как алфавит символов кодера меньше алфавита исходных (первичных) знаков, то каждому знаку соответствует некоторая последовательность символов, которую называют кодовой комбинацией.
Для операции сопоставления символов со знаками исходного алфавита используют термин "декодирование". Об этом говорит сайт https://intellect.icu . Техническая реализация этой операции осуществляется декодирующим устройством или декодером.
Передающее устройство осуществляет преобразование непрерывных сообщений или знаков в сигналы, удобные для прохождения по линии связи. При этом один или несколько параметров выбранного сигнала изменяют в соответствии с передаваемой информацией. Такой процесс называют модуляцией. Он осуществляется модулятором. Обратное преобразование сигналов в символы производится демодулятором. Под линией связи понимают среду (воздух, металл, магнитную ленту и т.д.), обеспечивающую поступление сигналов от передающего устройства к приемному устройству.
Сигналы на выходе линии связи могут отличаться от сигналов на ее входе (переданных) вследствие затухания, искажения и воздействия помех.
Помехами называют любые мешающие возмущения, как внешние, так и внутренние, вызывающие отклонение принятых сигналов от переданных сигналов.
Из смеси сигнала с помехой приемное устройство выделяет сигнал и посредством декодера восстанавливает сообщение, которое в общем случае может отличаться от посланного. Меру соответствия принятого сообщения посланному сообщению называют верностью передачи.
Принятое сообщение с выхода системы связи поступает к абоненту-получателю, которому была адресована исходная информация.
Совокупность средств, предназначенных для передачи сообщений, совместно со средой передачи называют каналом связи.
К теории информации относят следующие фундаментальные теоретические вопросы:
В теории информации исследуются информационные системы при четко сформулированных условиях :
В качестве основной характеристики сообщения теория информации принимает величину, называемую количеством информации. Это понятие не затрагивает смысл и важности передаваемого сообщения,а связано со степенью его неопределенности.
Пусть источник случайных сообщений выдает всего N различных символов или букв. Иногда этот набор символов называют алфавитом источника. Из этих символов или букв состоят сообщения на выходе источника. Длина отдельного сообщения произвольна, и может быть вообще не ограничена.
Введем теперь меру неопределенности появления определенного символ на выходе источника. Ее можно рассматривать и как меру количества информации, получаемой при появлении этого символа. Мера должна удовлетворять ряду естественных условий. Она должна возрастать с увеличением возможностей выбора, т. е. с увеличением числа N возможных символов на выходе источника. Тогда за меру неопределенности можно было бы взять число различных символов, предположив, что они равновероятны.
Таким образом, пусть на выходе источника случайных сообщений появляется сообщение произвольной длины, состоящее из N различных символов. Если все N символов источника являются равновероятными, то получение конкретного символа равносильно для него случайному выбору одного из N символов с вероятностью 1/N.
Ясно, что чем больше N, тем большая степень неопределенности характеризует этот выбор и тем более информативным можно считать сообщение, составленное из этих символов.
Поэтому число N могло бы служить мерой информативности источника.
Однако такая мера противоречит некоторым интуитивным представлениям. Например, при N=1, когда неопределенность появления символа отсутствует, она давала бы значение информативности, равное единице. Кроме того, такая мера не отвечает требованию аддитивности, состоящему в следующем. Если два независимых источника с числом равновероятных символов N и Μ рассматривать как один источник, одновременно реализующий пары символов NiMj, то естественно предположить, что информативность объединенного источника должна равняться сумме информативностей исходных источников. Поскольку общее число состояний объединенного источника равно ΝΜ, то искомая функция должна удовлетворять условию
I(N,M)=I(N)+I(M)
Требования выполняются, если в качестве меры информативности источника сообщений с равными вероятностями появления символов принять логарифм числа различных символов источника: Тогда приΝ= 1,I(U) = 0 и выполняется требование аддитивности для двух и более источников.
При этом в качестве меры неопределенности выбора ОДНОГО символа из источника с равновероятными появлением символов принимают логарифм числа символов источника:
H = logN
Эталогарифмическаяфункцияхарактеризуетколичество информации источника сообщений. Ее называют энтропией. Эта мера была предложена американским ученым Р.Хартли в 1928г.
В принципе безразлично, какое основание логарифма использовать для определения количества информации, так как в переход от одного основания логарифма к другому сводится лишь к изменению единицы измерения.
Так как современная информационная техника базируется на элементах, имеющих два устойчивых состояния, то обычно выбирают основание логарифма равным двум, т.е. информативность выражают как:
H = log2 N.
Тогда единицу количества информации на один символ источника называют двоичной единицей или битом.При этом единица неопределенности (двоичная единица или бит) представляет собой неопределенность выбора из двух равновероятных событий (bit — сокращение от англ binary digit — двоичная единица)
Так как из log2 N = 1 следует N = 2, то ясно, что один бит - это количество информации, которым характеризуется двоичный источник при равновероятных символах 0 и 1.
Двоичное сообщение такого источника длиной L содержит L бит информации.
Если основание логарифма выбрать равным десяти, то энтропия выражается в десятичных единицах на элемент сообщения - дитах, причем 1 дит = lg2 бит = 3,32 бит.
Пример.Определить количество информации, которое содержится в телевизионном сигнале, соответствующем одному кадру развертки.Пусть в кадре 625 строк, а сигнал, соответствующий одной строке, представляет собой последовательность из 600 случайных по амплитуде импульсов, причем амплитуда импульса может принять любое из 8 значений с шагом в 1 В.
Решение. В рассматриваемом случае длина сообщения (символа), соответствующая одной строке, равна числу случайных по амплитуде импульсов в ней: n = 600.
Количество символов (различных значений амплитуды) равно числу значений, которое может принять амплитуда импульсов в строке,: N = 8.
Количество информации в одной строке: Iстр. =600 logN= 600 log 8, а количество информации в кадре: Isum= 625*Iстр = 625 *600 log 8 = 1,125 • 106 бит
Рассмотренная выше оценка информативности или энтропия основана на предположении о равновероятности всех знаков алфавита. В общем же случае каждый из символов появляется в сообщении источника с различной вероятностью.
И что теперь делать? Как охарактеризовать информативность или меру неопределенности такого источника? Рассмотрим пути решения этой проблемы.
Пусть на основании статистического анализа известно, что в сообщении достаточно большой длины n знак Хi появляется n; раз, т.е. вероятность появления знака Хi
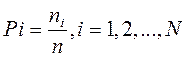
Все знаки алфавита этого источника составляют полную систему случайных событий, поэтому:
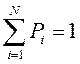
Введем понятие частной энтропии или неопределенности появления ОДНОГО конкретного i-того символа такого источника:
Hi=-log(Pi)
Тогда, взвесив ВСЕ частные энтропии вероятностями их появления Pi , можно записать выражения для средней энтропии , приходящейся на ОДИН символ источника.
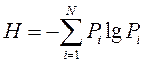
Эта средняя энтропия характеризует нам ВЕСЬ источник, его среднюю энтропию на один символ
Эта мера энтропии была введена Клодом Шенноном. Она полностью удовлетворяет нашим интуитивным требованиям к мере информации. Она аддитивна, при вероятностях появления символов источника, равных 1 и 0 она тоже равна 0.
Если сообщение источника состоит из n независимых символов, то суммарное количество информации в этом сообщении
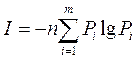
Вдальнейшемввыраженияхдляколичества информации Iи энтропии Н всегда используют логарифмы с основанием 2,
При равновероятности знаков алфавита Pi = 1/N из формулы Шеннона получают:
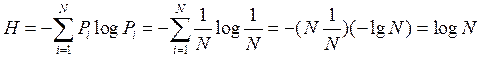
Из этого следует, что при равновероятности символов алфавита энтропия определяется исключительно числом символов алфавита и по существу является характеристикой только числа символов алфавита.
Если же знаки алфавита не равновероятны, то алфавит можно рассматривать как дискретную случайную величину, заданную статистическим распределением частот появления знаков Xi(или вероятностей Pi =ni / n) табл. 1:1
Таблица 1.1
|
Символы Xi |
X1 |
X2 |
… |
Xm |
|
Вероятности Pi |
P1 |
P2 |
… |
Pm |
Такие распределения получают обычно на основе статистического анализа конкретных типов сообщений (например, русских или английских текстов и т.п.).
Поэтому, если знаки алфавита не равновероятны и хотя формально в выражение для энтропии входят вероятности появления его знаков, энтропия отражает статистические свойства некоторой совокупности сообщений.
Еще раз вернемся к понятию энтропии источника сообщений.
В выражении для энтропии
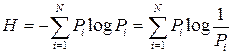
величина log 1/Pi представляет частную энтропию, характеризующую информативность знака хi, а энтропия Н - есть среднее значение частных энтропий. Таким образом, еще раз подчеркнем, что энтропия H источника выражает СРЕДНЮЮ энтропию на один символ алфавита.
Функция (Pi • log Pi) отражает вклад знака Xi в энтропию Н. При вероятности появления знака Pi=1 эта функция равна нулю, затем возрастает до своего максимума,а при дальнейшем уменьшении Pi стремится к нулю
Энтропия Н - величина вещественная, неотрицательная и ограниченная, т.е. Н > 0 (это свойство следует из того, что такими же качествами обладают все ее слагаемые Pi log (1/Pi).
Энтропия равна нулю, если сообщение известно заранее (в этом случае каждый элемент сообщения замещается некоторым знаком с вероятностью, равной единице, а вероятности остальных знаков равны нулю).
Энтропия максимальна, если все знаки алфавита равновероятны, т.е. Нmах = log N.
Таким образом, степень неопределенности источника информации зависит не только от числа состояний, но и от вероятностей этих состояний. При не равновероятных состояниях свобода выбора источника ограничивается, что должно приводить к уменьшению неопределенности. Если источник информации имеет, например, два возможных состояния с вероятностями 0,99 и 0,01, то неопределенность выбора у него значительно меньше, чем у источника, имеющего два равновероятных состояния. Действительно, в первом случае результат практически предрешен (реализация состояния, вероятность которого равна 0,99), а во втором случае неопределенность максимальна, поскольку никакого обоснованного предположения о результате выбора сделать нельзя. Ясно также, что весьма малое изменение вероятностей состояний вызывает соответственно незначительное изменение неопределенности выбора.
Особый интерес представляют бинарные источники, использующие алфавит из двух знаков: (0,1), При N = 2 сумма вероятностей знаков алфавита: P1+Р0 = 1. Можно положить P1 = Р, тогда Р0 = 1-Р.
Энтропию можно определить по формуле:
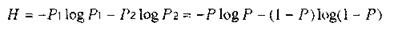
Энтропия бинарных сообщений достигает максимального значения, равного 1 биту, когда знаки алфавита сообщении равновероятны, т.е. при Р 0,5 ее график симметричен относительно этого значения, (рис.3).
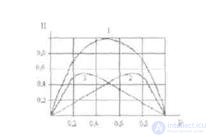
Рис. 1.3. График зависимости энтропии Н двоичных сообщений и ее составляющих : - (1 - Р) log (1 - Р) и - Р log P от Р.
Пример Заданы ансамбли X и Y двух дискретных величин
Таблица 1.2

Таблица 1.3.

Сравнить их энтропии.
Решение: Энтропия не зависит от конкретных значений случайной величины. Так как вероятности их появления в обоих случаях одинаковы, то
Н(Х) = H(Y) = ∑Pi*log(Pi)= - 4(0,251og0,25) = -4(l/41ogl/4) -= log 4=2 бит/c.
Надеюсь, эта статья про предмет теории информации, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое предмет теории информации, количественная мера информации, свойства энтропии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Теория информации и кодирования
Термины: Теория информации и кодирования