Привет, сегодня поговорим про подстановочные алгоритмы сжатия информации, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое подстановочные алгоритмы сжатия информации, словарно-ориентированные алгоритмы сжатия информации, методы лемпела-зива , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

12.1 Подстановочные или словарно-ориентированные алгоритмы сжатия информации . методы лемпела-зива .

Алгоритмы кодирования информации, которые приводят к уменьшению длины кода, относительно исходной длины сообщения, называют алгоритмами сжатия информации, а такое кодирование называют кодированием со сжатием.

Мы с вами, на самом деле, уже знакомы с кодами такого рода. Это коды Шеннона –Фано и Хаффмена которые называют оптимальным неравномерными кодами с переменной длиной слова. Если мы кодируем , например текстовое сообщение без учета вероятности появления символов, то на каждый знак мы можем тратить до 8 бит ( если знаки определяются таблицей ASCII). Знание статистики появления знаков позволяет сократить количество битов на знак алфавита в среднем до величины энтропии источника.

Методы кодирования Шеннона-Фэно, Хаффмена обобщающе называют статистическими методами, так как они используют вероятности появления отдельных слов или символов в источнике сообщений для получения эффекта сжатия. Словарные алгоритмы носят более практичный характер. Ихпреимущество перед статистическими теоретически объясняется тем, что они позволяют экономно кодировать последовательности символов разной длины без знания статистики источника сообщений.

Практическивсесловарныеметодыкодированияоснованы наалгоритмах описанных вработе двух израильских ученых - Зива и Лемпела, опубликованной в 1977 году. Сущность их состоит в том, что фразы в сжимаемом тексте заменяются указателем (или ссылкой) на то место, где онив этом тексте уже встречались.

Одной из причин популярности алгоритмов LZ является их исключительная простота при высокой эффективности сжатия.

Этот метод быстpо приспосабливается к стpуктуpе текста и может кодировать короткими указателями теслова, которые часто появляются в тексте. Новые слова и фразы могут также кодироваться частями ранее встреченных слов путем их замены на их указатели или номера.

Декодирование сжатого текста осуществляется напрямую - происходит простая замена указателя готовой фразой из словаря, на которую тот указывает. На практикеLZ-метод добивается хорошего сжатия, его важным свойством является очень быстрая работадекодера. (Когда мы говорим о тексте, то предполагаем, что кодированию подвергается некоторый набор данных с конечным дискретным алфавитом, и это не обязательно текст в буквальном смысле этого слова.)

Все словарные методы кодирования вида LZ можно разбить на две группы.

Первая группа с неявным видом словаря – основаалгоритм LZ77

Методы, принадлежащие к первой группе,находят в кодируемой последовательности цепочки символов, которые ранее уже встречались, и вместо того, чтобы повторять эти цепочки, заменяют их указателями на предыдущие повторения этих цепочек.

Словарьв этой группе алгоритмов в неявном виде содержится в обрабатываемых данных, сохраняются лишь указатели на встречающиеся цепочки повторяющихся символов.

Все алгоритмы из этой группы базируются на алгоритмеLZ77. Наиболее совершенным представителем этой группы, включившим в себя все достижения, полученные в данном направлении, является алгоритм LZSS,опубликованный в 1982 годуСторером и Шимански.

Процедура кодирования в соответствии с алгоритмами этой группы иллюстрируется примером 12.1.

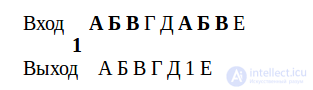
Пример 12.1

произошло сжатие за счет повторяющегося куска текста А Б В.

Алгоритмы второй группы на основе метода LZ78 используют словарь в явном виде

Алгоритмы второй группы в дополнение к исходному словарю источника в ходе сжатия-кодирования создают словарь фраз, представляющих собой повторяющиеся комбинации символов исходного словаря, которыевстречаются во входных данных. При этом размер словаря источника возрастает, и для его кодирования потребуется большее число бит, но значительная часть этого словаря будет представлять собой уже не отдельные буквы, а буквосочетания или целые слова.Когда кодер обнаруживает фразу, которая ранее уже встречалась, он заменяет ее индексом этой фразы в словаре. При этом длина кода индекса получается меньше или намного меньше длины кода фразы.

Все методы этой группы базируются на алгоритме, разработанном и опубликованном Лемпелем и Зивом в 1978 году, – LZ78. Наиболее совершенным на данный момент представителем этой группы словарных методов является алгоритм LZW, разработанный в 1984 году Терри Вэлчем.

Идеюэтойгруппыалгоритмовможно также пояснить с помощью примера 12.2.

Пример 12.2

12.2 LZ-алгоритмы упаковки данных :LZ77.

Рассмотрим алгоритм работы кодировщика сжатия по алгоритму LZ77 более подробно.

Основная идея LZ77 состоит в том, что второе и последующие вхождения некоторой строки символов в сообщении заменяются ссылками на ее первое вхождение.

LZ77 использует уже просмотренную часть сообщения как словарь. Чтобы добиться сжатия, он пытается заменить очередной фрагмент сообщения на указатель этого фрагмента в словаре.

LZ77 использует "скользящее" по сообщению окно, разделенное на две неравные части. Первая, большая по размеру, включает уже просмотренную часть сообщения. Это текущий словарь кодировщика, откуда он берет повторяющиеся куски. Вторая, намного меньшая, является буфером, содержащим еще незакодированные символы входного потока. Обычно размер окна словаря составляет несколько килобайт, а размер буфера - не более ста байт. Алгоритм пытается найти в скользящем по тексту словаре фрагмент, совпадающий с содержимым буфера или части буфера.

Алгоритм LZ77 выдает коды, состоящие из трех элементов:

• смещение в словаре относительно его начала подстроки, совпадающей с началом содержимого буфера;
• длина этой подстроки;
• первый символ буфера, следующий за подстрокой.

Пример. 12.3 Закодировать по алгоритму LZ77 строку "КРАСНАЯ КРАСКА".

В 9-й строке необходим сдвиг на5позиций (длина совпадающей строки +1) и считывание стольких же символов в буфер.

В последней строчке, буква "А" берется не из словаря, т.к. она последняя.

Длина кода вычисляется следующим образом: длина подстроки не может быть больше размера буфера, а смещение не может быть больше размера словаря минус единица. Следовательно, длина двоичного кода смещения будет округленным в большую сторону log2(размер словаря), а длина двоичного кода для длины подстроки будет округленным в большую сторону log2(размер буфера+1). А символ кодируется 8 битами (например в таблице ASCII+).

В последнем примере длина полученного кода равна 9*(3+3+8)=126 бит, против 14*8=112 бит исходной длины строки.

LZ77-алгоритм распаковки данных.

Пример 12.4

1. LZ77, длина словаря - 8 байт (символов). Коды сжатого сообщения

-

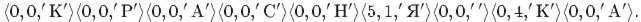
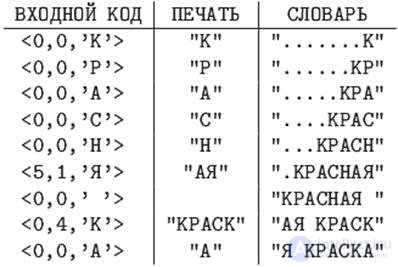
Недостатки LZ77:

LZ77 обладает следующими очевидными недостатками:

• 1. длина подстроки, которую можно закодировать, ограничена размером буфера.
• 2. с ростом размеров словаря скорость работы алгоритма-кодера пропорционально замедляется;
• 3. кодирование одиночных символов очень неэффективно.

Кодирование одиночных символов можно сделать эффективным, отказавшись от ненужной ссылки на словарь для них. Кроме того, в некоторые модификации LZ77 для повышения степени сжатия добавляется возможность для кодирования идущих подряд одинаковых символов.

Если механически чрезмерно увеличивать размеры словаря и буфера, то это приведет к снижению эффективности кодирования, т.к. с ростом этих величин будут расти и длины кодов для кодирования смещения и длины, что сделает коды для коротких подстрок недопустимо большими.

12.3 LZ-алгоритмы упаковки данных :LZ78.

В 1978 г. авторами LZ77 был разработан алгоритм LZ78, лишенный названных недостатков.

LZ78 не использует "скользящее" окно, он хранит словарь из уже просмотренных фраз. При старте алгоритма этот словарь содержит только одну пустую строку (строку длины нуль). Алгоритм считывает символы сообщения до тех пор, пока накапливаемая подстрока входит целиком в одну из фраз словаря. Как только эта строка перестанет соответствовать хотя бы одной фразе словаря, алгоритм генерирует код, состоящий из индекса строки в словаре, которая до последнего введенного символа содержала входную строку, и символа, следующего за совпадением. Затем в словарь добавляется введенная подстрока. Если словарь уже заполнен, то из него предварительно удаляют менее всех используемую в сравнениях фразу.

Ключевым для размера получаемых кодов является размер словаря во фразах, потому что каждый код при кодировании по методу LZ78 содержит номер фразы в словаре. Из последнего следует, что эти коды имеют постоянную длину, равную округленному в большую сторону двоичному логарифму размера словаря+8 (это количество бит в байт-коде расширенного ASCII).

Пример 12.5.

Закодировать по алгоритму LZ78 строку "КРАСНАЯ КРАСКА", используя словарь длиной 16 фраз.

Указатель на любую фразу такого словаря - это число от 0 до 15, для его кодирования достаточно четырех бит.

LZ-алгоритмы распаковки данных. Пример 13.6

LZ78, длина словаря - 16 фраз. Коды сжатого сообщения -

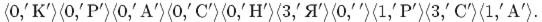
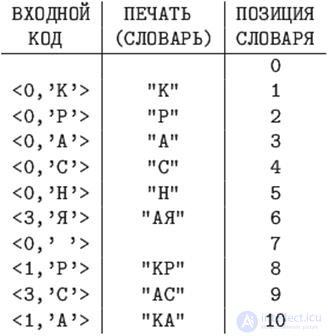
В последнем примере длина полученного кода равна 10*(4+8)=120битам.

Алгоритмы LZ77, LZ78 и могут использоваться свободно.

В 1984 г. Уэлчем (Welch) был путем модификации LZ78 создан алгоритм LZW, более эффективный чем его прототип. Алгоритм LZW используется как основа во многих известных и эффективных программах сжатия данных программах – архиваторах.

Методы Лемпела-Зива.

Алгоритм Лемпеля — Зива — Велча

Алгоритм Лемпеля — Зива — Уэлча (Lempel-Ziv-Welch, LZW) — это универсальный алгоритм сжатия данных без потерь, созданный Авраамом Лемпелем (англ. Abraham Lempel), Яаковом Зивом (англ. Jacob Ziv) и Терри Велчем (англ. Terry Welch). Он был опубликован Велчем в 1984 году в качестве улучшенной реализации алгоритма LZ78, опубликованного Лемпелем и Зивом в 1978 году . Алгоритм разработан так, чтобы его было достаточно просто реализовать как программно, так и аппаратно .

Акроним «LZW» указывает на фамилии изобретателей алгоритма: Лемпель, Зив и Велч, но многие утверждают, что, поскольку патент принадлежал Зиву, то метод должен называться алгоритмом Зива — Лемпеля — Велча.

Описание

Данный алгоритм при кодировании (сжатии) сообщения динамически создает словарь фраз: определенным последовательностям символов (фразам) ставятся в соответствие группы битов (коды) фиксированной длины (например, 12-битные, как предлагается в исходной статье Велча ). Словарь инициализируется всеми 1-символьными фразами (в случае 8-битных символов — это 256 фраз). По мере кодирования алгоритм просматривает текст символ за символом слева направо. При чтении алгоритмом очередного символа в данной позиции находится строка W максимальной длины, совпадающая с какой-то фразой из словаря. Затем код этой фразы подается на выход, а строка WK, где K — это символ, следующий за W во входном сообщении, вносится в словарь в качестве новой фразы и ей присваивается какой-то код (так как W выбрана жадно, WK еще не содержится в словаре). Символ K используется в качестве начала следующей фразы. Более формально данный алгоритм можно описать следующей последовательностью шагов:

1. Инициализация словаря всеми возможными односимвольными фразами. Инициализация входной фразы W первым символом сообщения.
2. Если КОНЕЦ_СООБЩЕНИЯ, то выдать код для W и завершить алгоритм.
3. Считать очередной символ K из кодируемого сообщения.
4. Если фраза WK уже есть в словаре, то присвоить входной фразе W значение WK и перейти к Шагу 2.
5. Иначе выдать код W, добавить WK в словарь, присвоить входной фразе W значение K и перейти к Шагу 2.

Алгоритму декодирования на входе требуется только закодированный текст: соответствующий словарь фраз легко воссоздается посредством имитации работы алгоритма кодирования (но есть неочевидные нюансы, обсуждаемые в примере ниже).

Реализация

Примечательной особенностью алгоритма LZW является простота реализации, благодаря которой он до сих пор очень популярен, несмотря на зачастую худшую степень сжатия по сравнению с такими аналогами, как LZ77 . Обычно LZW реализуется с помощью префиксного дерева, содержащего фразы из словаря: для нахождения W нужно просто прочитать как можно более длинную строку из корня дерева, затем для добавления новой фразы WK нужно присоединить к найденному узлу нового сына по символу K, а кодом фразы W может выступать индекс узла в массиве, содержащем все узлы.

Кодирование фраз

Использование для фраз кодов фиксированной длины (12 битов в описании Велча ) может негативно сказаться на эффективности сжатия, так как, во-первых, для начальных кодируемых символов этот подход скорее будет раздувать данные, а не сжимать (если символ занимает 8 битов), и во-вторых, общий размер словаря (2¹²=4096) получается не так велик. Первая проблема решается кодированием выходной последовательности алгоритмом Хаффмана (возможно, адаптивным) или арифметическим кодированием. Для решения второй используют другие подходы.

Первый простой вариант — применить какой-нибудь оптимальный универсальный код типа кода Левенштейна или кода Элиаса. В таком случае теоретически словарь может расти неограниченно.

Другой более распространенный вариант — изменять максимальный возможный размер словаря с ростом числа фраз. Изначально, например, максимальный размер словаря полагается 2⁹ (2⁸ кодов при этом уже заняты фразами для кодирования 8-битовых одиночных символов) и на код фразы отводится 9 битов. Когда число фраз становится 2⁹, максимальный размер становится 2¹⁰ и на коды отводится 10 битов. И так далее. Таким образом, теоретически словарь может быть сколь угодно большим. Этот метод продемонстрирован в примере ниже (обычно, тем не менее, максимальный размер словаря ограничивается; например в LZC — популярной модификации LZW, рассматриваемой ниже — длины кодов растут от 9 до 16 битов.).

В большинстве реализаций последнего метода число битов, выделяемых на код фразы, увеличивается до добавления новой фразы WK, переполняющей словарь, но после записи на выход кода W. Например, пусть в данный момент в процессе работы алгоритма длина кода — p битов, и алгоритм собирается выдать код фразы W и добавить новую фразу WK в словарь; если код WK равен 2^p (то есть WK переполняет словарь), то сначала выдается p-битовый код W и только после этого p увеличивается на один, чтобы последующие коды занимали p+1 битов. Среди ранних реализаций LZW существуют такие, которые увеличивают p до выдачи кода W, то есть код W, выдаваемый перед добавлением WK в словарь, уже занимает p+1 битов (что не является необходимым, так как код W меньше 2^p). Об этом говорит сайт https://intellect.icu . Такое поведение называется «ранним изменением» (early change). Эта путаница в реализациях побудила Adobe поддерживать оба варианта LZW в PDF (используются ли «ранние изменения», указывается с помощью специального флага в заголовке сжимаемых данных).

Переполнение словаря

Так как коды в алгоритме LZW имеют фиксированную длину, размер словаря ограничен (при использовании кодов нефиксированной длины размер словаря ограничен объемом доступной памяти). Возникает вопрос: что делать в случае переполнения словаря? Используют несколько стратегий.

1. Самый очевидный вариант — просто использовать построенный словарь без дальнейших модификаций. Ясно, что часто это плохая стратегия.
2. Авторы некогда популярной утилиты compress^[en] просто используют построенный словарь, пока степень сжатия остается приемлемой, а затем очищают его в случае ухудшения качества сжатия. Такая модификация LZW называется LZC (Lempel-Ziv-Compress, см. ниже).
3. П. Тисчер предложил перед вставкой в переполненный словарь новой фразы на очередном шаге алгоритма удалять из словаря фразу, которая дольше всего не использовалась (LRU, Least Recently Used). Такая модификация иногда называется LZT (Lempel-Ziv-Tischer, см. ниже).

Пример

Данный пример показывает алгоритм LZW в действии, показывая состояние выходных данных и словаря на каждой стадии, как при кодировании, так и при раскодировании сообщения. С тем чтобы сделать изложение проще, мы ограничимся простым алфавитом — только заглавные буквы, без знаков препинания и пробелов. Сообщение, которое нужно сжать, выглядит следующим образом:

TOBEORNOTTOBEORTOBEORNOT#

Маркер # используется для обозначения конца сообщения. Тем самым, в нашем алфавите 27 символов (26 заглавных букв от A до Z и #). Компьютер представляет это в виде групп бит, для представления каждого символа алфавита нам достаточно группы из 5 бит на символ. По мере роста словаря, размер групп должен расти, с тем чтобы учесть новые элементы. 5-битные группы дают 2⁵ = 32 возможных комбинации бит, поэтому, когда в словаре появится 33-е слово, алгоритм должен перейти к 6-битным группам. Заметим, что, поскольку используется группа из всех нулей 00000, то 33-я группа имеет код 32. Начальный словарь будет содержать:

# = 00000
A = 00001
B = 00010
C = 00011
.
.
.
Z = 11010

Кодирование

Без использования алгоритма LZW, при передаче сообщения, как оно есть — 25 символов по 5 бит на каждый — оно займет 125 бит. Сравним это с тем, что получается при использовании LZW:

Символ:  Битовый код:  Новая запись словаря:
         (на выходе)

T      20 =  10100
O      15 =  01111     27: TO
B       2 =  00010     28: OB
E       5 =  00101     29: BE
O      15 =  01111     30: EO
R      18 =  10010     31: OR <--- со следующего символа начинаем использовать 6-битные группы 
N      14 = 001110     32: RN
O      15 = 001111     33: NO
T      20 = 010100     34: OT
TO     27 = 011011     35: TT
BE     29 = 011101     36: TOB
OR     31 = 011111     37: BEO
TOB    36 = 100100     38: ORT
EO     30 = 011110     39: TOBE
RN     32 = 100000     40: EOR
OT     34 = 100010     41: RNO
#       0 = 000000     42: OT#

Общая длина = 6*5 + 11*6 = 96 бит.

Таким образом, используя LZW, мы сократили сообщение на 29 бит из 125 — это почти 22 %. Если сообщение будет длиннее, то элементы словаря будут представлять все более и более длинные части текста, благодаря чему повторяющиеся слова будут представлены очень компактно.

Декодирование

Теперь представим, что мы получили закодированное сообщение, приведенное выше, и нам нужно его декодировать. Прежде всего, нам нужно знать начальный словарь, а последующие записи словаря мы можем реконструировать уже на ходу, поскольку они являются просто конкатенацией предыдущих записей.

Данные:     На выходе:     Новая запись:
                        Полная:      Частичная:
10100  = 20     T                    27: T?
01111  = 15     O       27: TO       28: O?
00010  = 2      B       28: OB       29: B?
00101  = 5      E       29: BE       30: E?
01111  = 15     O       30: EO       31: O?  
10010  = 18     R       31: OR       32: R? <---- начинаем использовать 6-битные группы
001110 = 14     N       32: RN       33: N?
001111 = 15     O       33: NO       34: O?
010100 = 20     T       34: OT       35: T?
011011 = 27     TO      35: TT       36: TO? <---- для 37, добавляем только первый элемент
011101 = 29     BE      36: TOB      37: BE?      следующего слова словаря
011111 = 31     OR      37: BEO      38: OR?
100100 = 36     TOB     38: ORT      39: TOB?
011110 = 30     EO      39: TOBE     40: EO?
100000 = 32     RN      40: EOR      41: RN?
100010 = 34     OT      41: RNO      42: OT?
000000 = 0      #

Единственная небольшая трудность может возникнуть, если новое слово словаря пересылается немедленно. В приведенном выше примере декодирования, когда декодер встречает первый символ, T, он знает, что слово 27 начинается с T, но чем оно заканчивается? Проиллюстрируем проблему следующим примером. Мы декодируем сообщение ABABA:

Данные:     На выходе:     Новая запись:
                        Полная:      Частичная:
.
.
.
011101 = 29     AB      46: (word)   47: AB?
101111 = 47     AB?  <--- что нам с этим делать?

На первый взгляд, для декодера это неразрешимая ситуация. Мы знаем наперед, что словом 47 должно быть ABA, но как декодер узнает об этом? Заметим, что слово 47 состоит из слова 29 плюс символ, идущий следующим. Таким образом, слово 47 заканчивается на «символ, идущий следующим». Но, поскольку это слово посылается немедленно, то оно должно начинаться с «символа, идущего следующим», и поэтому оно заканчивается тем же символом, что и начинается, в данном случае — A. Этот трюк позволяет декодеру определить, что слово 47 — это ABA.

В общем случае, такая ситуация появляется, когда кодируется последовательность вида cScSc, где c — это один символ, а S — строка, причем слово cS уже есть в словаре.

Теоретическая оценка эффективности

Теоретические свойства LZW с неограниченным словарем в целом такие же, как и у LZ78, и анализ этих двух методов сжатия аналогичен. При рассмотрении неограниченного словаря естественно предполагать, что выходные фразы кодируются кодами переменной длины, например, каким-нибудь универсальным кодом или фиксированным кодом, размер которого растет вместе с максимальным размером словаря (см. раздел о реализации).

Отношение к энтропии сжимаемых данных

Асимптотическая оптимальность

Для теоретической оценки эффективности данный метод сжатия сравнивают с некоторой эталонной метрикой. К сожалению, идеальная эталонная метрика сжатия данных — Колмогоровская сложность — невычислима даже приблизительно, и поэтому любой алгоритм сжатия заведомо проигрывает в сравнении с ней. Лемпель и Зив предложили ослабленную версию Колмогоровской сложности — сжатие конечными автоматами . По техническим причинам данная метрика определяется для бесконечных строк. Зафиксируем конечный алфавит . Пусть дана бесконечная строка над . Обозначим через число битов в кодировке LZW с неограниченным словарем для строки . Отсюда имеем

где — это число фраз в LZW кодировке для . Зив показал , что

где — это метрика сжатия конечными автоматами, определенная далее . Таким образом, коэффициент сжатия LZW (отношение к — числу битов, занимаемых несжатой строкой) асимптотически ограничен и в этом смысле LZW оптимален. Более того, если размер словаря ограничен и при переполнении используется стратегия удаления наименее используемых фраз, LZW также асимптотически оптимален в следующем смысле:

где обозначает число битов в кодировке LZW со словарем, в котором содержатся не более фраз, каждая фраза имеет длину не больше и при переполнении словаря выбрасывается реже всего использовавшаяся фраза (этот вариант похож на LZT; см. модификации). Отметим, что аналогичными свойствами обладают алгоритмы LZ78 и LZ77 (включая аналогичные варианты, соответственно, со словарем и скользящим окном ограниченного размера) . Определим теперь .

Метрика во многом аналогична Колмогоровской сложности, но вместо полноценных машин Тьюринга в ее определении используются машины Тьюринга с конечной памятью, то есть конечные автоматы. Для данного числа обозначим через множество всех детерминированных автоматов Мили которые имеют состояний и перекодируют строки над алфавитом в бинарные последовательности, так что по выходу автомата можно восстановить исходную строку; более точно, на ребрах автомата записаны бинарные строки (возможно пустые), так что по любой конечной строке над алфавитом автомат приходит в некоторое состояние и в процессе выдают бинарную последовательность , и по последовательности и состоянию можно однозначно восстановить (чтобы сжимающий автомат мог иметь пустые строки на ребрах, строка восстанавливается не только по последовательности , но и по конечному состоянию ). Для данной бесконечной строки определим:

где обозначает число битов в . Таким образом, представляет собой оценку на наименьший возможный коэффициент сжатия, которого можно достигнуть при сжатии строки конечными автоматами. Заметим, что из-за неограниченности словаря алгоритм LZW не может быть смоделирован с помощью автомата Мили, в отличие от алгоритма LZW с ограниченным словарем с не более чем фразами длины не более (размер такого автомата Мили, естественно, зависит от ).

Неоптимальность числа фраз

Метрика сжатия конечными автоматами, хоть и является естественной, не так эффективна, как может показаться на первый взгляд. Так, асимптотически оптимальным по отношению к является любой алгоритм сжатия, который разбивает данную строку на различные фразы (то есть при ) и затем кодирует , используя битов . Ясно, что алгоритм, удовлетворяющий таким слабым критериям, вовсе не обязан быть эффективным на практике. Вдобавок, метрика сжатия конечными автоматами не отражает способности многих методов сжатия заменять длинные повторяющиеся фрагменты в данных ссылками на место, где такой фрагмент встретился впервые (у конечного автомата просто не достанет памяти для сравнения длинных фрагментов). Именно этот механизм зачастую является причиной эффективности сжатия больших объемов данных на практике, и как показано далее, LZW (и LZ78) достаточно плохо справляются с данной задачей в худшем случае по сравнению, например, с LZ77.

Алгоритм LZW с неограниченным размером словаря разлагает данную конечную строку на фразы , так что каждая фраза либо является символом, либо равна , где — какое-то число меньшее , а — это первый символ фразы . Существуют и другие разложения вида для строки и естественно возникает вопрос: насколько хорошо разложение, построенное жадным алгоритмом LZW?

Пусть обозначает минимальное число, такое что строка представима в виде разложения , в котором каждая строка либо является символом, либо равна , где — какое-то число меньшее , а — первый символ строки . Сержио Де Агостино и Рикардо Сильвестри^[10] доказали, что в худшем случае может быть больше в раза, даже если алфавит содержит всего лишь два символа (они также показали, что то есть данная оценка оптимальна). Иными словами, жадная стратегия дает в данном случае результаты очень далекие от оптимальных. Частично оправдывает подход LZW то, что построение оптимального разложения с фразами является NP-полной задачей, как показали Де Агостино и Сторер^[11].

Другой естественный вопрос: насколько хорош LZW по сравнению с LZ77? Известно, что LZ77 жадным образом разлагает строку на фразы , так что каждая фраза либо является символом, либо является подстрокой строки . Хуке, Лори, Ре^[12] и Чарикар и др.^[13] показали, что в худшем случае может быть в раз больше, чем . С другой стороны, известно, что всегда не меньше , и даже более того, всегда не меньше .^[13] Иными словами, LZW и даже «оптимальная» версия LZW, содержащая фраз, не может быть лучше LZ77 (по крайней мере существенно — обратите внимание, что здесь обсуждается число фраз, а не способ их кодирования), а в некоторых патологических случаях может быть катастрофически хуже.

Применение

На момент своего появления алгоритм LZW давал лучший коэффициент сжатия для большинства приложений, чем любой другой хорошо известный метод того времени. Он стал первым широко используемым на компьютерах методом сжатия данных.

Алгоритм (а точнее его модификация, LZC, см. ниже) был реализован в программе compress^[en], которая стала более или менее стандартной утилитой Unix-систем приблизительно в 1986 году. Несколько других популярных утилит-архиваторов также используют этот метод или близкие к нему.

В 1987 году алгоритм стал частью стандарта на формат изображений GIF. Он также может (опционально) использоваться в формате TIFF. Помимо этого, алгоритм применяется в протоколе модемной связи v.42bis и стандарте PDF^[14] (хотя по умолчанию большая часть текстовых и визуальных данных в PDF сжимается с помощью алгоритма Deflate).

Патенты

На алгоритм LZW и его вариации был выдан ряд патентов, как в США, так и в других странах. На LZ78 был выдан американский патент U.S. Patent 4 464 650, принадлежащий Sperry Corporation, позднее ставшей частью Unisys Corporation. На LZW в США были выданы два патента: U.S. Patent 4 814 746, принадлежащий IBM, и патент Велча U.S. Patent 4 558 302 (выдан 20 июня 1983 года), принадлежащий Sperry Corporation, позднее перешедший к Unisys Corporation. К настоящему времени сроки всех патентов истекли.

Unisys, GIF и PNG

При разработке формата GIF в CompuServe не знали о существовании патента U.S. Patent 4 558 302. В декабре 1994 года, когда в Unisys стало известно об использовании LZW в широко используемом графическом формате, эта компания распространила информацию о своих планах по взысканию лицензионных отчислений с коммерческих программ, имеющих возможность по созданию GIF-файлов. В то время формат был уже настолько широко распространен, что большинство компаний-производителей ПО не имели другого выхода, кроме как заплатить. Эта ситуация стала одной из причин разработки графического формата PNG (неофициальная расшифровка: «PNG’s Not GIF»^[15]), ставшего третьим по распространенности в WWW, после GIF и JPEG. В конце августа 1999 года Unisys прервала действие безвозмездных лицензий на LZW для бесплатного и некоммерческого ПО^[16], а также для пользователей нелицензированных программ, понудив League for Programming Freedom развернуть кампанию «сожжем все GIF’ы»^[17] и информировать публику об имеющихся альтернативах. Многие эксперты в области патентного права отмечали, что патент не распространяется на устройства, которые могут лишь разжимать LZW-данные, но не сжимать их; по этой причине популярная утилита gzip может читать .Z-файлы, но не записывать их.

20 июня 2003 года истек срок оригинального американского патента, что означает, что Unisys не может больше собирать по нему лицензионные отчисления. Аналогичные патенты в Европе, Японии и Канаде истекли в 2004 году.

Модификации

• LZC (1985, Thomas S. W., McKie J., Davies S., Turkowski K., Woods J. A. и Orost J. W.) — одна из наиболее известных практических реализаций LZW, представленная в утилите compress^[en] (Lempel-Ziv-Compress). LZC использует от 9 до 16 битов для кодов фраз (число битов растет с ростом размера словаря, см. раздел о реализации); когда словарь переполняется, LZC просто продолжает его использование без дальнейшей модификации, но при этом алгоритм следит за степенью сжатия данных и, когда сжатие с текущим словарем становится неприемлемо плохим, LZC очищает словарь и продолжает работу. LZC сжимает хуже, чем LZW, но зато скорость сжатия выше.
• LZT (1985, Tischer P.) — другой известный вариант LZW. При переполнении словаря LZT продолжает работу, но каждый раз перед вставкой новой фразы в словарь, он удаляет фразу, которая соответствует дольше всего не используемому листу в префиксном дереве, содержащем все фразы. В реализации LZT все листья помещаются в связный список, и каждый раз после использования в ходе сжатия листья перемещаются в голову списка; таким образом, листья, которые не использовались дольше всего, находятся в хвосте списка (дальнейшие детали очевидны).
• LZMW (1985, Виктор Миллер^[en] и Марк Вегман )^[18] — находит во входном потоке самую длинную строку, которая уже имеется в словаре (обозначим ее W), выдает на выход код W, а затем добавляет в словарь строку VW, где V — это строка из словаря, код которой был выдан на предыдущем шаге (изначально V является пустой строкой). Таким образом, строки в словаре растут быстрее, чем в исходном варианте LZW, и на практике часто удается получить лучшее качество сжатия. Миллер и Вегман также предложили в случае недостатка памяти удалять из словаря фразы, которые редко используются, так же как это делается в LZT.
• LZAP (1988, Джеймс Сторер)^[19] — модификация LZMW, отличающаяся тем, что на каждом шаге в словарь добавляется не только строка VW, но и строки VW₁, VW₂, …, VW_|W|-1, где W_i — это префикс W длины i. («AP» в «LZAP» означает «all prefixes», то есть «все префиксы».) Например, если V = wiki и W = pedia — то есть на предыдущем шаге алгоритм нашел в словаре строку wiki, а на данном нашел pedia — то алгоритм добавит в словарь строку wikipedia, как сделал бы LZMW, но также добавит строки wikip, wikipe, wikiped, wikipedi. Алгоритм LZAP проще для реализации, чем LZMW, но в то же время он сохраняет большинство преимуществ LZMW за исключением того, что коды словарных строк занимают больше места, потому что словарь более раздут.

Контрольные вопросы.

• 1. Назовите основные цели кодирования со сжатием информации.
• 2. Основной прием при кодировании со сжатием.
• 3.Чем отличается метод кодирования LZ77 от метода кодирования LZ78?
• 4. Какой из методов кодирования LZ77 или LZ78 потенциально более эффективен?
• 5. Назовите основные недостатки метода LZ77.

Вау!! 😲 Ты еще не читал? Это зря!

• LZ
• LZ77
• LZMA

Надеюсь, эта статья про подстановочные алгоритмы сжатия информации, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое подстановочные алгоритмы сжатия информации, словарно-ориентированные алгоритмы сжатия информации, методы лемпела-зива и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.