Лекция
Привет, Вы узнаете о том , что такое арифметическое кодирование, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое арифметическое кодирование , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.
арифметическое кодирование — один из алгоритмов энтропийного сжатия.
В отличие от алгоритма Хаффмана, не имеет жесткого постоянного соответствия входных символов группам бит выходного потока. Это дает алгоритму большую гибкость в представлении дробных частот встречаемости символов.
Как правило, превосходит алгоритм Хаффмана по эффективности сжатия, позволяет сжимать данные с энтропией, меньшей 1 бита на кодируемый символ, но некоторые версии имеют патентные ограничения от компании IBM.
Обеспечивает почти оптимальную степень сжатия с точки зрения энтропийной оценки кодирования Шеннона. На каждый символ требуется почти бит, где
— информационная энтропия источника.
В отличие от алгоритма Хаффмана, метод арифметического кодирования показывает высокую эффективность для дробных неравномерных интервалов распределения вероятностей кодируемых символов. Однако в случае равновероятного распределения символов, например, для строки бит 010101…0101 длины s метод арифметического кодирования приближается к префиксному коду Хаффмана и даже может занимать на один бит больше.
Пусть имеется некий алфавит, а также данные о частотности использования символов (опционально). Тогда рассмотрим на координатной прямой отрезок от 0 до 1.
Назовем этот отрезок рабочим. Расположим на нем точки таким образом, что длины образованных отрезков будут равны частоте использования символа, и каждый такой отрезок будет соответствовать одному символу.
Теперь возьмем символ из потока и найдем для него отрезок среди только что сформированных, теперь отрезок для этого символа стал рабочим. Разобьем его таким же образом, как разбили отрезок от 0 до 1. Выполним эту операцию для некоторого числа последовательных символов. Затем выберем любое число из рабочего отрезка. Биты этого числа вместе с длиной его битовой записи и есть результат арифметического кодирования использованных символов потока.
Используя метод арифметического кодирования, можно достичь почти оптимального представления для заданного набора символов и их вероятностей (согласно теории энтропийного кодирования источника Шеннона оптимальное представление будет стремиться к числу −log2P бит на каждый символ, вероятность которого P). Алгоритмы сжатия данных, использующие в своей работе метод арифметического кодирования, перед непосредственным кодированием формируют модель входных данных на основании количественных или статистических характеристик, а также, найденных в кодируемой последовательности повторений или паттернов — любой дополнительной информации, позволяющей уточнить вероятность появления символа P в процессе кодирования. Очевидно, что чем точнее определена или предсказана вероятность символа, тем выше эффективность сжатия.
Рассмотрим простейший случай статической модели для кодирования информации, поступающей с системы обработки сигнала. Типы сигналов и соответствующие им вероятности распределены следующим образом:
Появление последнего символа для декодера означает, что вся последовательность была успешно декодирована (в качестве альтернативного подхода, но необязательно более успешно, можно использовать блочный алгоритм фиксированной длины).
Следует также отметить, что в качестве алфавита вероятностной модели метода можно рассматривать любой набор символов, исходя из особенностей решаемой задачи. Об этом говорит сайт https://intellect.icu . Более эвристические подходы, использующие основную схему метода арифметического кодирования, применяют динамические или адаптивные модели. Идея данных методов заключается в уточнении вероятности кодируемого символа за счет учета вероятности предшествующего или будущего контекста (то есть, вероятность появления кодируемого символа после определенного k-го числа символов слева или справа, где k — это порядок контекста).
Возьмем для примера следующую последовательность:
NEUTRAL NEGATIVE END-OF-DATA
Сначала разобьем отрезок от 0 до 1 согласно частотам сигналов. Разбивать отрезок будем в порядке, указанном выше: NEUTRAL — от 0 до 0,6; POSITIVE — от 0,6 до 0,8; NEGATIVE — от 0,8 до 0,9; END-OF-DATA — от 0,9 до 1.
Теперь начнем кодировать с первого символа. Первому символу — NEUTRAL соответствует отрезок от 0 до 0,6. Разобьем этот отрезок аналогично отрезку от 0 до 1.
Закодируем второй символ — NEGATIVE. На отрезке от 0 до 0,6 ему соответствует отрезок от 0,48 до 0,54. Разобьем этот отрезок аналогично отрезку от 0 до 1.
Закодируем третий символ — END-OF-DATA. На отрезке от 0,48 до 0,54 ему соответствует отрезок от 0,534 до 0,54.
Так как это был последний символ, то кодирование завершено. Закодированное сообщение — отрезок от 0,534 до 0,54 или любое число из него, например, 0,538.
Предположим, что нам необходимо раскодировать сообщение методом арифметического кодирования согласно описанной выше модели. Сообщение в закодированном виде представлено дробным значением 0,538 (для простоты используется десятичное представление дроби, вместо двоичного основания). Предполагается, что закодированное сообщение содержит ровно столько знаков в рассматриваемом числе, сколько необходимо для однозначного восстановления первоначальных данных.
Начальное состояние процесса декодирования совпадает с процессом кодирования и рассматривается интервал [0,1). На основании известной вероятностной модели дробное значение 0,538 попадает в интервал [0, 0,6). Это позволяет определить первый символ, который был выбран кодировщиком, поэтому его значение выводится как первый символ декодированного сообщения.
Арифметическое кодирование является методом, позволяющим упаковывать символы входного алфавита без потерь при условии, что известно распределение частот этих символов. Арифметическое кодирование является оптимальным, достигая теоретической границы степени сжатия. Арифметическое кодирование – блочное и выходной код является уникальным для каждого из возможных входных сообщений; его нельзя разбить на коды отдельных символов, в отличие от кодов Хаффмана, которые являются неблочными, т.е. каждой букве входного алфавита ставится в соответствие определенный выходной код.
Текст, сжатый арифметическим кодером, рассматривается как некоторая двоичная дробь из интервала [0, 1). Результат сжатия можно представить как последовательность двоичных цифр из записи этой дроби. Каждый символ исходного текста представляется отрезком на числовой оси с длиной, равной вероятности его появления и началом, совпадающим с концом отрезка символа, предшествующего ему в алфавите. Сумма всех отрезков, очевидно должна равняться единице. Если рассматривать на каждом шаге текущий интервал как целое, то каждый вновь поступивший входной символ “вырезает” из него подинтервал пропорционально своей длине и положению.
Построение интервала для сообщения "АБВГ...":
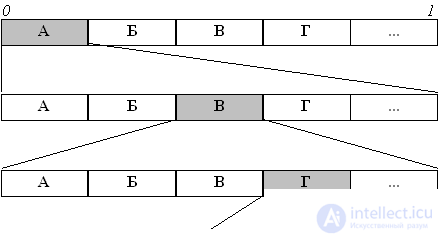 |
Поясним работу метода на примере:
Пусть алфавит состоит из двух символов: “a” и “b” с вероятностями соответственно 3/4 и 1/4.
Рассмотрим (открытый справа) интервал [0, 1). Разобьем его на части, длина которых пропорциональна вероятностям символов. В нашем случае это [0, 3/4) и [3/4, 1). Суть алгоритма в следующем: каждому слову во входном алфавите соответствует некоторый подинтервал из [0, 1). Пустому слову соответствует весь интервал [0, 1). После получения каждого очередного символа арифметический кодер уменьшает интервал, выбирая ту его часть, которая соответствует вновь поступившему символу. Кодом сообщения является интервал, выделенный после обработки всех его символов, точнее, число минимальной длины, входящее в этот интервал. Длина полученного интервала пропорциональна вероятности появления кодируемого текста.
Выполним алгоритм для цепочки “aaba”:
| Шаг | Просмотренная цепочка | Интервал |
| 0 | “” | [0, 1) = [0, 1) |
| 1 | “a” | [0, 3/4) = [0, 0.11) |
| 2 | “aa” | [0, 9/16) = [0, 0.1001) |
| 3 | “aab” | [27/64, 36/64) = [0.011011, 0.100100) |
| 4 | “aaba” | [108/256, 135/256) = [0.01101100, 0.10000111) |
На первом шаге мы берем первые 3/4 интервала, соответствующие символу "а", затем оставляем от него еще только 3/4. После третьего шага от предыдущего интервала останется его правая четверть в соответствии с положением и вероятностью символа "b". И, наконец, на четвертом шаге мы оставляем лишь первые 3/4 от результата. Это и есть интервал, которому принадлежит исходное сообщение.
В качестве кода можно взять любое число из диапазона, полученного на шаге 4. Возникает вопрос: "А где же здесь сжатие? Исходный текст можно было закодировать четырьмя битами, а мы получили восьмибитный интервал". Дело в том, что в качестве кода мы можем выбрать, например, самый короткий код из интервала, равный 0.1 и получить четырехкратное сокращение объема текста. Для сравнения, код Хаффмана не смог бы сжать подобное сообщение, однако, на практике выигрыш обычно невелик и предпочтение отдается более простому и быстрому алгоритму из предыдущего раздела.
Арифметический декодер работает синхронно с кодером: начав с интервала [0, 1), он последовательно определяет символы входной цепочки. В частности, в нашем случае он вначале разделит (пропорционально частотам символов) интервал [0, 1) на [0, 0.11) и [0.11, 1). Поскольку число 0.1 (переданный кодером код цепочки "aaba") находится в первом из них, можно получить первый символ: "a". Затем делим первый подинтервал [0, 0.11) на [0, 0.1001) и [0.1001, 0.1100) (пропорционально частотам символов). Опять выбираем первый, так как 0 < 0.1 < 0.1001. Продолжая этот процесс, мы однозначно декодируем все четыре символа.
При рассмотрении этого метода возникают две проблемы: во-первых, необходима вещественная арифметика, вообще говоря, неограниченной точности, и во-вторых, результат кодирования становится известен лишь при окончании входного потока. Дальнейшие исследования, однако, показали, что можно практически без потерь обойтись целочисленной арифметикой небольшой точности (16-32 разряда), а также добиться инкрементальной работы алгоритма: цифры кода могут выдаваться последовательно по мере чтения входного потока.
Подобно алгоритму Хаффмана, арифметический кодер также является двухпроходным и требует передачи вместе с закодированным текстом еще и таблицы частот символов. Вообще, эти алгоритмы очень похожи и могут легко взаимозаменяться. Следовательно, существует адаптивный алгоритм арифметического кодирования со всеми вытекающими достоинствами и недостатками. Его основное отличие от статического в том, что новые интервалы вероятности перерассчитываются после получения каждого следующего символа из входного потока.
Исследование, описанное в статье про арифметическое кодирование, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое арифметическое кодирование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования
Комментарии
Оставить комментарий
Теория информации и кодирования
Термины: Теория информации и кодирования