Методы кодирования со сжатием и с потерями информации. JPEG

Привет, сегодня поговорим про методы кодирования со сжатием, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое методы кодирования со сжатием, с потерями информации jpeg , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

Тема9. Методы кодирования со сжатием и с потерями информации.

15.1 Методы сжатия с потерей информации.

Как уже ранее отмечалось, существуют два типа систем сжатия данных:

 ·                  без потерь информации

 ·                    с потерями информации

Прикодировании без потерь исходные данные могут быть восстановлены из сжатых в первоначальном виде, то есть абсолютно точно. Такое кодирование применяется для сжатия текстов, баз данных, компьютерных программ и данных и т.п., где недопустимо их даже малейшееразличие.Все рассмотренные выше методы кодирования относились именно к кодированию без потерь.

К сожалению, сжатие или кодирование без потерь, когда имеется полное совпадение исходных и восстановленных данных, имеет невысокую эффективность – коэффициентысжатия редко превышают 3…5 (за исключением случаев кодирования данных с высокой степенью повторяемости одинаковых участков и т.п.).

15.2 Точность. Помехи и искажения. Приближенное восстановление.

Точность. Вместе с тем очень часто нет необходимости в абсолютной точности передачи исходных данных потребителю. Во-первых, сами источники данных обладают ограниченным динамическим диапазоном и вырабатывают исходные сообщения с определенным уровнем искажений и ошибок. Этот уровень может быть большим или меньшим, но абсолютной точности воспроизведения достичь невозможно.

Помехи и искажения. Во-вторых, передача данных по каналам связи и их хранение всегда производятся при наличии различного рода помех. Поэтому принятое (воспроизведенное) сообщение всегда в определенной степени отличается от переданного, то есть на практике невозможна абсолютно точная передача при наличии помех в канале связи (в системе хранения).

Восприимчивость. Наконец, сообщения передаются и сохраняются для их восприятия и использования получателем. Получатели же информации - органы чувств человека, исполнительные механизмы и т.д. - также обладают конечной разрешающей способностью, то есть не замечают незначительной разницы между абсолютно точным и приближенным значениями воспроизводимого сообщения. Порог чувствительности к искажениям также может быть различным, но он всегда есть.

Приближенное восстановление. Кодирование с потерями учитывает эти аргументы в пользу приближенного восстановления данных и позволяет получить за счет некоторой контролируемой по величине ошибки коэффициенты сжатия,иногда в десятки раз превышающие степень сжатия для методов без потерь.

Предварительное преобразование. Большинство методов сжатия с потерями основано на кодировании не самихданных, а некоторых линейных преобразований от них, например, коэффициентов дискретного преобразования Фурье ( ДПФ ), коэффициентов косинусного преобразования, преобразований Хаара, Уолшаи т.п.

Для того, чтобы понять, на чем основана высокая эффективность системсжатияс потерями и почему кодирование преобразований оказывается значительно более эффективным, нежели кодирование исходных данных, рассмотрим в качестве примера популярный метод сжатия изображений JPEG ( “джипег” ), который содержит в себе все необходимые признаки системысжатия с потерями.Не будем сейчас вдаваться в формульные дебри, главное – понять идею кодирования преобразований.

Нужно будет также рассмотреть и сущностьсамих линейных преобразований, применяемых для сжатия, поскольку без понимания их физического смысла трудно уяснить причины получаемых эффектов.

15.3 Кодирование преобразований. Стандарт сжатия JPEG.

Популярный стандарт кодирования изображений JPEG ( Joint Photographers Experts Group ) является очень хорошей иллюстрацией к объяснению принципов сжатие с потерями на основе кодирования преобразований.

Для сжатия графической информации с потерями в конце 1980-х установлен один стандарт - формат JPEG (Joint Photographic Experts Group - название объединения его разработчиков). В этом формате можно регулировать степень сжатия, задавая степень потери качества.

Простое уменьшение разрядности. Основную идею кодирования преобразований можно понять из следующих простых рассуждений. Допустим, мы имеем дело с некоторым цифровым сигналом (последовательностью отсчетов Котельникова). Если отбросить в каждом из отсчетов половину двоичных разрядов (например, 4 разряда из восьми), товдвое уменьшится объем кода R и потеряется половина информации, содержащейся в сигнале.

ДПФ и простое уменьшение разрядности. Если же подвергнуть сигнал преобразованию Фурье (или какому-либо другому подобному линейному преобразованию), разделить его на две составляющие – НЧ и ВЧ, продискретизовать, подвергнуть квантованию каждую из них и отбросить половину двоичных разрядов только в высокочастотной составляющей сигнала, то результирующая объем кода уменьшится на одну треть, а потеря информации составит всего 5%.

Этот эффект обусловлен тем, что низкочастотные составляющие большинства сигналов (крупные детали) обычно гораздо более интенсивны и несут гораздо больше информации, нежели высокочастотные составляющие (мелкие детали). Это в равной степени относится и к звуковым сигналам, и к изображениям.

Рассмотрим работу алгоритма сжатия JPEG при кодировании черно-белого изображения, представленного набором своих отсчетов (пикселов)с числом градаций яркостив 256 уровней (8 двоичных разрядов). Это самый распространенный способ храненияизображений - каждой точке на экране соответствует один байт (8 бит - 256 возможных значений), определяющий ее яркость. 255 - яркость максимальная (белый цвет), 0 - минимальная (черный цвет). Промежуточные значения составляют всю остальную гамму серых цветов(рис. 15.1).

<![endif]><![if !RotText]><![endif]><![if !vml]> 

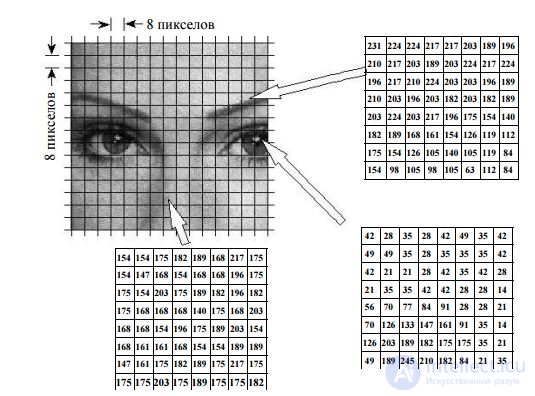
Рис. 15.1

Работа алгоритма сжатия JPEG  начинается с разбиения изображения на квадратные блоки размером 8х8 = 64 пиксела. Почему именно 8х8, а не 2х2 или 32х32 ? Выбор такого размера блока обусловлен тем, что при его малом размере эффект сжатия будет небольшим (при размере 1х1 – вообще отсутствует), а при большом - свойства изображения в пределах блока будут сильно изменяться и эффективность кодирования снова снизится.

На рис. 15.1 изображено несколько таких блоков (в виде матриц цифровых отсчетов), взятых из различных участков изображения. В дальнейшем эти блоки будут обрабатываться и кодироваться независимо друг от друга.

Второй этап сжатия – применение ко всем блокамдискретного косинусного преобразования – DCT. Для сжатия данных пытались применить множество различных преобразований, в том числе специально разработанных для этих целей, например, преобразование Карунены-Лоэва, обеспечивающее максимально возможный коэффициент сжатия. Но оно очень сложно реализуется на практике. Преобразование Фурье выполняется очень просто, но не обеспечивает хорошего сжатия. Выбор был остановлен на дискретном косинусном преобразовании, являющем разновидностью ПФ. В отличие от ПФ, которое применяет для разложения сигнала синусные и косинусные частотные составляющие, в DCT используются только косинусные составляющие. Дискретное косинусное преобразование позволяет перейти от пространственного представления изображения (набором отсчетов или пикселов) к спектральному представлению (набором частотных составляющих) и наоборот.

Дискретное косинусное преобразование от изображения

IMG ( x, y )может быть записано следующим образом:

где N = 8,0 < i < 7 , 0 < j < 7,

или же, в матричной форме,

RES= DCT ^T*IMG * DCT,

где DCT- матрица базисных (косинусных) коэффициентов для преобразования размером 8х8,имеет конкретный вид:

Обратное восстановление матрицы пикселей исходного изображения IMG по его преобразованию DCT в матричной форме имеет очевидный вид:

IMG = DCT*RES * DCT ^T

Итак, в результате применения к блоку изображенияразмером 8х8 пикселовдискретного косинусного преобразования получим двумерный спектр, также имеющий размер8х8 отсчетов.Иными словами, 64 числа, представляющие отсчеты изображения, превратятся в 64 числа, представляющие отсчеты его DCT-спектра.

А теперь напомним, что такое спектр сигнала. Это – величины коэффициентов, с которыми соответствующие спектральные составляющие входят в сумму, которая в результате и дает этот сигнал.Отдельные спектральные составляющие, на которые раскладывается сигнал, часто называют базисными функциями. Для преобразования Фурье базисными функциями являются синусы и косинусы разных частот.

Для8х8 DCT система базисных функцийзадается формулой

  ,

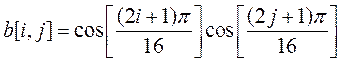Сами базисные функции выглядят подобно приведенным на рис. 15.2. для одномерного DCT преобразования для n=4, 8, 16. Рисунок дает нам понятие о качественных характеристиках преобразования или разложения входного сигнала на спектральные составляющие. По характеру поведения базисных функций видно, что функции с наименьшими номерами выделяют из спектра сигнала низкочастотные составляющие, а с ростом номера функции она выделяет все более высокочастотные компоненты сигнала.

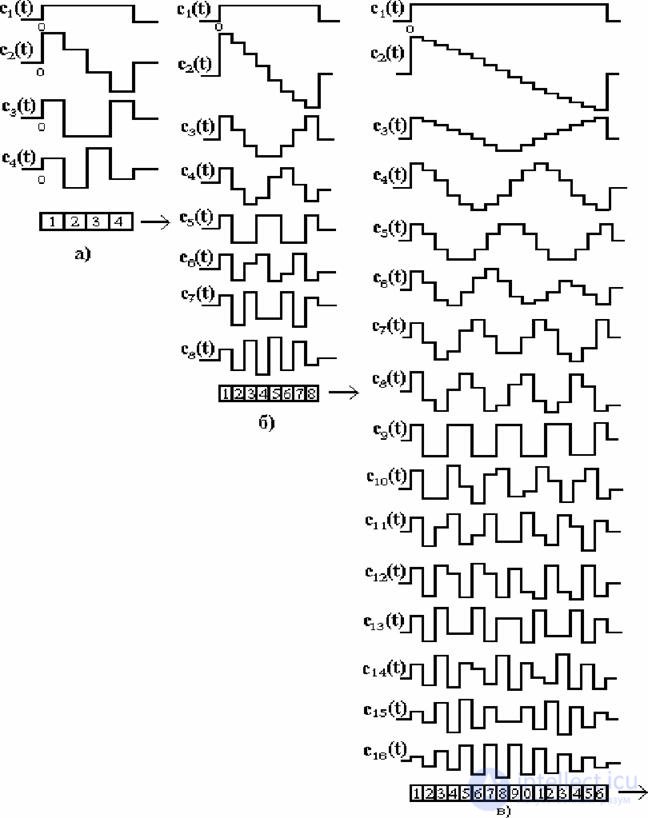
Рис. 15.2

На рис. 15.3 показано поведение базисных функций двумерного DCT для n=4. Нетрудно заметить, что сечение каждого квадратика по горизонтали совпадает с поведением одномерной DCT для n=4для ситуации рис.15.2

Рис. 15.3

Самая низкочастотная базисная функция, соответствующая индексам (0,0), изображена в левом верхнем углу рисунка, самая высокочастотная – в нижнем правом. Базисная функция для (0,1) представляет собой половину периода косинусоиды по одной координате и константу - по другой, базисная функция с индексами (1,0) – то же самое, но повернута на 90⁰ .

Дискретное косинусное преобразование вычисляется путем поэлементного перемножения и суммированияблоков изображения 8х8 пикселов с каждой из этих базисных функций. В результате, к примеру, компонента DCT-спектра с индексами (0,0) будет представлять собой просто сумму всех элементов блока изображения, то есть среднюю для блока яркость. В компоненту с индексом (0,1) усредняются с одинаковыми весами все горизонтальные детали изображения, а по вертикали наибольший вес присваивается элементам верхней части изображения и т.д. Можно заметить, что чем ниже и правее в матрице DCT  его компонента, тем более высокочастотным деталям изображения она соответствует.

Для того, чтобы получить исходное изображение по его DCT-спектру (выполнить обратное преобразование), нужно теперь базисную функцию с индексами (0,0) умножить на спектральную компоненту с координатами (0,0), прибавить к результату произведение базисной функции (1,0) на спектральную компоненту (1,0) и т.д.

В приведенной ниже табл. 15.1 приведенычисловые значения одного из блоков изображенияи его DCT-спектра:

Таблица 15.1

Отметимочень интересную особенность полученного DCT-спектра: наибольшие его значения сосредоточены в левом верхнем углу табл. Об этом говорит сайт https://intellect.icu . 15.1 (низкочастотные составляющие), правая же нижняя его часть (высокочастотные составляющие) заполнена относительнонебольшими числами. Чисел этих, правда, столько же, как и в блоке изображения: 8х8 = 64, то есть пока никакого сжатия не произошло, и, если выполнить обратноепреобразование, получим тот же самый блок изображения.

Следующим этапом работы алгоритма JPEG является квантование (табл. 15.2).

Если внимательно посмотреть на полученные в результате DCT коэффициенты, то будет видно, что добрая их половина - нулевые илиимеет очень небольшие значения (1 - 2). Это высокие частоты, которые (обычно) могут быть безболезненно отброшены или, по крайней мере, округлены до ближайшего целого значения.

Квантование заключается в делении каждого коэффициентаDCT на некоторое число в соответствии с матрицей квантования. Эта матрица может быть фиксированной либо, для более качественного и эффективного сжатия, получена в результате анализа характера исходной картинки.Чем больше числа, на которые происходит деление, тем большев результате деления будет нулевых значений, а значит, сильнее сжатие и заметнее потери.

Таблица 15.2

Совершенно очевидно, что от выбора таблицы квантования будет в значительной степени зависеть как эффективность сжатия – число нулей в квантованном (округленном) спектре ,– так и качество восстановленной картинки.

Таким образом, мы округлили результат DCT и получили в большей или меньшей степени искаженныйпоблочный спектр изображения.

Следующим этапом работы алгоритма JPEG является преобразование 8х8 матрицы DCT-спектра в линейную последовательность. Но делается это таким образом, чтобы сгруппировать по возможности вместе вначале все большие значения и потом все нулевые значения спектра. Совершенно очевидно, что для этого нужно прочесть элементы матрицы коэффициентов DCT в порядке, изображенном на рис. 15.4, то есть зигзагообразно - из левого верхнего угла к правому нижнему.

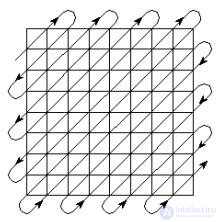
Рис. 15.4

Эта процедура называется зигзаг-сканированием.

В результате такого преобразования квадратная матрица 8х8 квантованных коэффициентов DCT превратится в линейную последовательность из 64 чисел, большая часть из которых – это идущие подряд нули. Известно, что такие потоки можно очень эффективно сжимать путем кодирования длин повторений. Именно так это и делается.

На следующем, пятом этапе JPEG-кодирования получившиеся цепочки нулей подвергаются кодированию длин повторений.

Наконец, последним этапом работы алгоритма JPEG является кодирование получившейся последовательности каким-либо статистическим алгоритмом или алгоритмам из серии LZW. Обычно используетсякодирование по методу Шеннона-Фано или по алгоритму Хаффмена.В результате получается новая последовательность, размер которой существенно меньше размера массива исходных данных.

Последние два этапа кодирования обычно называют вторичным сжатием, и именно здесь происходитстатистическое кодирование без потерь, и с учетом характерной структуры данных - существенное уменьшение их объема.

Декодирование данных сжатых согласно алгоритму JPEG производится точно так же, как и кодирование, но все операции следуют в обратном порядке.

После распаковки методом Хаффмена (или LZW) и расстановки линейной последовательности в блоки размером 8х8 чисел спектральные компонентыдеквантуются с помощью сохраненных при кодировании таблиц квантования. Для этого распакованные 64 значенияDCT умножаются на соответствующие числа из таблицы. После этого каждый блок подвергается обратному косинусному преобразованию, процедура которого совпадает с прямым и различается только знаками в матрице преобразования. Последовательность действий при декодировании и полученный результат иллюстрируются приведенной ниже табл. 16.3.

Таблица 15.3

Очевидно, что восстановленные данные несколько отличаются от исходных. Это естественно, потому что JPEG и разрабатывался, как сжатие с потерями.

На представленном ниже рис. 15.5 приведено исходное изображение(слева) , а также изображение, сжатое с использованием алгоритма JPEG в 10 раз (в центре) и в 45 раз (справа). Потеря качества в последнем случае вполне заметна, но и выигрыш по объему тоже очевиден.

Рис. 15.5

Итак,JPEG-сжатие состоит из следующих этапов:

 1.    Разбиение изображения на блоки размером 8х8 пикселов.

 2.    Применение к каждому из блоков дискретного косинусного преобразования.

 3.    Округление коэффициентов DCT в соответствии с заданной матрицей весовых коэффициентов.

 4.   Преобразование матрицы округленных коэффициентов DCTв линейную последовательность путем их зигзагообразного чтения.

 5.    Кодирование повторений для сокращения числа нулевых компонент.

 6.               Статистическое кодирование результата кодом Хаффмена или арифметическим кодом.

Декодирование производится точно так же, но в обратном порядке.

Существенными положительными сторонами алгоритма сжатия JPEG являются:

-возможность задания в широких пределах (от 2 до 200) степени сжатия;

-возможность работы с изображениями любой разрядности;

-симметричность процедур сжатия – распаковки.

К недостаткам можно отнести наличие ореола на резких переходах цветов - эффект Гиббса, а также распадение изображения на отдельные квадратики 8х8 при высокой степени сжатия.

15.4 Контрольные вопросы.

1. Назовите виды исходной информации, которые можно кодировать с потерями.

2. Почему в методах кодирования с потерями производится предварительное преобразование (ДПФ) информации?

3. Назовите основные этапы кодирования изображений по методу JPEG.

4. Почему в качестве базового элемента сжатияпо методу JPEG выбрана матрица 8Х8 пикселов изображения?

5. Какой должна быть матрица квантования в методе JPEG, если мы не хотим терять информацию в изображении?

Надеюсь, эта статья про методы кодирования со сжатием, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое методы кодирования со сжатием, с потерями информации jpeg и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.