Эффективное кодирование источника дискретных сообщений в канале без помех

Привет, сегодня поговорим про эффективное кодирование источника дискретных сообщений в канале без помех, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое эффективное кодирование источника дискретных сообщений в канале без помех , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

Тема3. Эффективноекодированиеисточникадискретныхсообщенийвканалебезпомех.

Лекция3.

3.1Избыточностьинформации, причиныеепоявления.

Для нахождения максимальной пропускной способности системы связи необходимо уметь определять максимальное количество информации, которое может быть передано при помощи символов данного алфавита за единицу времени. Известно, что максимальное количество информации на символ сообщения H=logN можно получить только в случае равновероятных и независимых символов. Реальные источники сообщений редко полностью удовлетворяют этому условию, поэтому информационная нагрузка на каждый их символ обычно меньше той, которую они могли бы переносить.

Как правило символы первичного источника при передаче в канал связи подвергаются кодировке для приведения их к виду, необходимому для передачи в канал, например кодируются в двоичный код. При этом одному первичному символу соответствует кодовое слово кодера первичного источника.

Поскольку информационная нагрузка на каждый символ первичного источника обычно меньше той, которую они могли бы переносить, то символы информационно недогружены и само сообщение обладает информационной избыточностью.

Понятие избыточности в теории информации и кодирования введено для количественного описания информационного резерва кода, из которого составлено сообщение. Сама постановка такой задачи стала возможной именно потому, что информация является измеримой величиной, каков бы ни был частный вид рассматриваемого сообщения.

Статистическая избыточность обусловливается неравновероятностным распределением символов первичного алфавита и их взаимозависимостью.

Например, для английского алфавита, состоящего из 26 букв, максимальное значение энтропии

H_max=log₂m=log₂26=4,7 бит

 

При учете частоты появления букв в текстах, передаваемую информацию можно значительно сжать, сократить.

Отношение μ=H/Н_mах называют коэффициентом сжатии, или относительной энтропией, а величину

<![if !vml]><![endif]>

избыточностью.

 

Из этого выражения очевидно, что избыточность меньше у тех сообщений, у которых больше энтропия первичного алфавита.

Энтропия может быть определена как информационная нагрузка на символ сообщения. Избыточность определяет недогруженность символов. Если Н = H_mах, то согласно выражению недогруженности не существует и D=0.

В остальных случаях тем же количеством кодовых слов может быть предано большее символов. Например, кодовым словом их трех двоичных разрядов мы можем передать и 5 и 8 символов.

Фактически для передачи первичного символа в двоичном коде достаточно иметь длину кодовой комбинации при кодировании первичных символов.

<![if !vml]>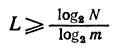<![endif]>

где N — общее количество передаваемых символов, m число символов вторичного алфавитов. Для N=5

 

<![if !vml]>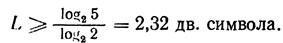<![endif]>

 

Однако эту цифру необходимо округлить до ближайшего целого числа, так как длина кода не может быть выражена дробным числом. Округление производится в большую сторону.

В общем случае избыточность от округления

<![if !vml]>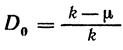<![endif]>

<![if !vml]><![endif]>

 

k — округленное до ближайшего целого значение µ.

Для нашего примера

 

<![if !vml]>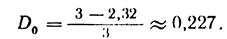<![endif]>

 

Цифра 0,227 характеризует степень недогруженности кода.

Рассмотрим, что можно сделать для уменьшения избыточности первичного алфавита (источника символов). Рассмотрим источник сообщений, выдающий символы А с вероятностью появления p(A)=0.9 и В с p(B)=0.1

В этом случае энтропия источника Н=0.47 бит/с, Н_мах=log2=1бит/с.

Избыточность D=1-(0.47/1)=0.53.

Как ее уменьшить?

 

3.2Способысокращенияизбыточности.

Выделим в сообщениях этого источника двуместные блоки вида AA, AB, BA, BB. Поскольку символы А и В независимы, то соответствующие вероятности их появления p(AA)=0.81, p(AB)=0.09, p(BA)=0.09, p(BB)=0.01. Об этом говорит сайт https://intellect.icu .

В этом случае N=4,

H=∑p_i*log(p_i)=1.14бит/сим,

H_max=2бит/с.

И избыточность

D=1-(1.14/2)=0.43.

Переход к поблочному (двухсимвольному) кодированию сообщений первичного источника уменьшил его избыточность. Можно показать, что при достаточно большой длине блока избыточность источника будет достаточно мала.

Избыточность, заложенную в природе первичного источника, полностью устранить нельзя. Однако избыточность от неравновероятного появления символов автоматически убывает по мере увеличения длины кодового блока.

Указанный прием уменьшения источника путем кодирования сообщений блоками является основой для определения потенциальных характеристик кодирования для каналов связи без помех.

 

Выводы: 1. Избыточность сообщений, составленных из равновероятных символов, меньше избыточности сообщений, составленных из не равновероятных символов.

2. Информационная статистическая избыточность первичного источника сообщений явление естественное и заложена такая избыточность в статистических характеристиках первичного алфавита.

3.Уменьшая избыточность сообщения, можно увеличить скорость его передачи по каналу связи.

 

Для дальнейшего изложения нам понадобится понятие производительности источника сообщений.

Что такое производительность источника. Пусть источник генерирует 1 символ за время τ=1 мксек. Тогда, если энтропия источника например 2бит/символ, то его производительность

Сист.=Н/τ=2Мбит/сек.

 

3.3ТеоремаШеннонадляканалабезпомех.

Система передачи информации, в которой аппаратура не вносит никаких искажений, а канал связи — затуханий и помех, называется информационной системой без шумов. В такой системе, как бы ни были закодированы сигналы, потерь информации не будет. Но это еще не значит, что в такой системе автоматически решаются все технические проблемы передачи информации. Для однозначного декодирования принятых сообщений, а также для передачи больших объемов информации при меньших временных и материальных затратах коды должны, в частности, удовлетворять следующим требованиям:

1. Разные символы первичного алфавита, из которого составлены сообщения, должны иметь paзличные кодовые комбинации.

2. Кoд должен быть построен так, чтобы можно было четко отделить начало и конец кодовых слов.

3. Код должен быть максимально коротким. Чем меньшее число элементарных символов кода требуется для передачи данного сообщения, тем ближе скорость передачи информации к скорости, которую теоретически можно достигнуть в данном канале связи.

Первое требование очевидно, так как при одинаковых кодовых словах для различных букв алфавитов нельзя будет их однозначно декодировать.

Второе требование может быть удовлетворено следующим образом:

-введением в код дополнительного разделительного символа - паузы, что значительно удлиняет коды, а следовательно, и время передачи сообщения;

- созданием кода, в котором конец одной кодовой комбинации не может быть началом другой;

- либо созданием кода, в котором все буквы передаются комбинациями равной длины, т. е. равномерного кода.

При этом следует отметить, что равномерные коды обладают известными преимуществами; длину каждой буквы можно определить простым подсчетом элементарных символов, что позволяет автоматизировать процесс декодирования и строить простые декодирующие устройства. Однако равномерные коды имеют один существенный недостаток: все кодовые слова алфавитов, представленных ими, имеют равную длину независимо от вероятности появления отдельных символов кодируемого алфавита. Такой код может быть оптимальным только для случая равновероятных и взаимонезависимых символов сообщений, что довольно часто встречается в телемеханике и никогда — при передаче текстовых сообщений.

Для того чтобы найти условия, удовлетворяющие третьему, основному, требованию к кодам, необходимо узнать, в каких пределах находится минимальная средняя длина кодового слова данного алфавита, а также найти условия, при которых эта длина может быть уменьшена.

Согласно N=mⁿ чтобы, передать N неповторяющихся сообщений при помощи m символов вторичного алфавита, их надо комбинировать по n штук в кодовом слове. В случае равновероятного первичного источника из N символов его энтропия

H=logN.

Очевидно, что при этом длина кодового слова кодера источника

n=logN/log(m).

Наша задача состоит в том, чтобы построить код для данного источника из N символов со средней длиной слова,.близкого к этому значению.

Для первичного источника сообщений с неравновероятным распределением символов на выходевозможный минимум средней длины кодового слова

 

L=H/log(m)

 

Так как на практике передавать приходится сообщения, составленные из алфавитов с некоторой реальной энтропией, и от разработчика системы связи не зависит ее увеличение или уменьшение непосредственно в первичном алфавите, то желательно таким образом кодировать символы первичного алфавита чтобы использовать информационный резерв, заложенный в первичном алфавите.

Эта идея была реализована в кодах, в которых избыточность, содержащаяся в первичном алфавите, полностью или практически полностью устраняется за счет рационального построения кодовых слов во вторичном алфавите.

В этом смысле предельно короткими являются так называемые оптимальные коды - коды с нулевой (или близкой к нулю) избыточностью. Классическим примером кода с нулевой избыточностью может быть код Шеннона – Фано., построение которых мы рассмотрим на следующих лекциях.

Таким образом величина

L=H/log(m)

может служить мерой длины кодового слова. Для случая, когда N является целой степенью числа 2,

N=2^k,

k — целое число и k представляет собой минимальную длину кодового слова L для кодирования символов первичного источника в двоичном алфавите.

Для двоичных алфавитов (m = 2)

 

_{<![if !vml]><![endif]>}

 

Для m-значного равновероятного алфавита длина кодового слова

_{<![if !vml]>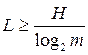<![endif]>}(А)

Подводя итоги, можно сказать, что в общем случае средняя минимальная длина кодового слова L для первичного источника из N символов, составленного из алфавита с m знаками

_{<![if !vml]>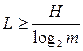<![endif]>}

С другой стороны можно показать что

_{<![if !vml]>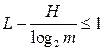<![endif]>}

или

_{<![if !vml]><![endif]>}(В)

Доказательство (см. например учебник Цымбала гл.14стр.113, 114) основано на очевидно понятном соотношении

[Х]-X<1,

где [X] -целая часть Х, то есть на том, что разность между округлением числа Х до целого в большую сторону и самим числом Х меньше 1.

Выражения (А) и (В) представляют собой соответственно верхнюю и нижнюю границы минимально необходимой средней длины кодового слова. Используя эти выражения, получаем

 

<![if !vml]>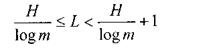<![endif]>(C).

Рассмотрим теперь условия, при которых будет уменьшаться разность между верхней и нижней границами, то есть условия, при которых средняя минимальная длина кодового слова будет приближаться к значению H/log(m).

Для этого сначала выясним природу избыточности, выражающейся неравенством

<![if !vml]>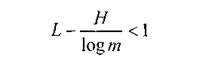<![endif]>

Предположим, что передаются равновероятные символы некоторого первичного алфавита при помощи равномерного двоичного кода m = 2. Для передачи восьми букв алфавита минимальная длина кодового слова

<![if !vml]><![endif]>

Для передачи пяти букв

 

L₂=log₂5=2.322

т. е. минимальная длина не может быть передана меньше, чем тремя символами. В этом случае коэффициент сжатия

 

µ=2.322/3=0.774

 

а избыточность

 

D=1-µ=1-0.774=0.226

 

Цифра 0,226 характеризует степень недогруженности кода. Выражение

 

<![if !vml]>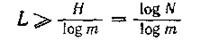<![endif]>

 

справедливо для кодов с равновероятными и взаимонезависимыми символами.

Рассмотрим теперь случай поблочного кодирования (смотри пример из первой части лекции, где каждый из блоков состоит из М независимых букв a₁,a₂,…,a_м ).

Выражение для энтропии сообщения из всех букв блока, согласно правилу сложения энтропии,

<![if !vml]><![endif]>

По аналогии с формулой (C) запишем выражение для средней длины такого кодового блока

<![if !vml]>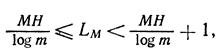<![endif]>

 

где L_М – среднее количество символов в блоке.

Для такого блочного кодирования, очевидно, имеет место соотношение

L_М=L*M,

тогда

L=Lм/M.

 

Нетрудно заметить, что теперь L можно получить, разделив все части неравенства (С) на М. Тогда общее выражение для среднего числа элементарных символов на кода на символ первичного источника сообщений

<![if !vml]>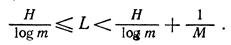<![endif]>(D)

 

Из этого видно, что при М → ∞ среднее число элементарных символов кодового слова, затрачиваемых на передачу одной буквы, неограниченно приближается к величине

_{<![if !vml]><![endif]>}

 

Выражение (D) является основным выражением фундаментальной теоремы кодирования Шеннона при отсутствии шумов. Сама теорема может быть сформулирована следующим образом:

При кодировании множества сигналов с энтропией Н в алфавите, насчитывающем m символов, при отсутствии шумов средняя длина кодового слова не может быть меньше, чем

_{<![if !vml]><![endif]>},

точное достижение указанной границы невозможно; но при кодировании достаточно длинными блоками к этой границе можно сколь угодно приблизиться.

 

Для двоичных кодов основную теорему кодирования можно сформулировать так: при кодировании, сообщений в двоичном алфавите с ростом количества кодовых слов среднее число двоичных знаков на символ исходного алфавита приближается к энтропии источника сообщений.

Если кодируемый алфавит равновероятный и N= 2ⁱ (где i — целое число), то среднее число двоичных знаков на букву в точности равно энтропии источника сообщений.

 

Выводы:

1. Чем длиннее первичное кодовое слово, тем точнее величина

_{<![if !vml]><![endif]>}

характеризует среднюю длину кодового слова.

2. Чем больше первичных символов в блоке, тем меньше разность между верхней и нижней границами, определяющими среднее число элементарных символов кода на букву сообщения.

3. Из какого бы числа букв ни состоял алфавит, целесообразно кодировать сообщения не побуквенно а поблочно.

4. Энтропия первичного алфавита может характеризовать возможный предел сокращения кодового слова во вторичном алфавите.

 

3.4Контрольныевопросы.

1. Назовите причины избыточности источников информации.

2. Назовите основные требования к кодам, уменьшающим избыточность первичного источника сообщений.

3. Сформулируйте основной практический вывод из теоремы Шеннона для кодирования в канале без помех.

Надеюсь, эта статья про эффективное кодирование источника дискретных сообщений в канале без помех, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое эффективное кодирование источника дискретных сообщений в канале без помех и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория информации и кодирования

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.