Лекция
Привет, сегодня поговорим про преобразования в двухмерном пространстве, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое преобразования в двухмерном пространстве, компьютерная графика , настоятельно рекомендую прочитать все из категории Компьютерная графика.
преобразования в двухмерном пространстве используются в разнообразных случаях: чтобы отдельные части объекта можно было описывать в различных координатных системах; чтобы типовые и повторяющиеся части можно было располагать в произвольных положениях на чертеже и в пространстве, в том числе с использованием циклов; чтобы без повторной кодировки можно было получать симметричные части объекта; для направленной деформации фигур, тел и их частей; для изменения масштаба чертежа, построения проекций пространственных образов... С аналитической точки зрения преобразования — это пересчет значений координат.
Точка на плоскости представляется двумя координатами: |x y|. Матрица преобразования точки выглядит так:

Ниже показано преобразование точки через квадратную матрицу; здесь xn = xa + yc и yn = xb + yd — новые координаты точки после преобразования:
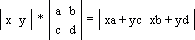
Если представить фигуру как совокупность точек, то можно провести и ее преобразование. В следующем примере задано четыре точки: A(0, 0), B(1, 0), C(1, 1), D(0, 1), каждая из которых после преобразования переходит соответственно в A*(0, 0), B*(a, b), C*(a + c, b + d), D*(c, d):
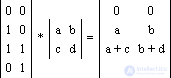
Геометрически это соответствует деформации фигуры:

При этом площадь новой фигуры равна площади старой фигуры, умноженной на детерминант матрицы преобразования: S2 = S1 * |ad - bc|.
Любая система координат, в которой представление точки в двухмерном (трехмерном) пространстве задается при помощи трех (четырех) координат (Р1, Р2, Р3(, Р4)), называется системой однородных координат. Вообще, для n-мерного пространства число однородных координат должно быть на единицу больше: n + 1.
Применение однородных координат в общем случае позволяет устранять аномалии, возникающие при работе в декартовых координатах, и представлять сложные преобразования в виде произведения нескольких матриц.
Геометрическая интерпретация на случай двухмерного пространства: введение третьей координаты, равной единице, можно трактовать как переход в трехмерное пространство, в котором разрешено работать только в плоскости z = 1. Следует представлять себе, что экран компьютера (картинная плоскость, плоскость изображения) находится в плоскости z = 1:

В случае выхода рисунка за сечение z = 1 рисунок возвращается принудительно в данное сечение — для того, чтобы были возможны последующие операции:
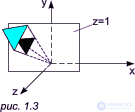
Такая операция называется нормализацией однородных координат:



Матрица преобразования содержит в себе константы m и n, под действием которых точка смещается на m единиц вдоль оси x и на n единиц — вдоль оси y:


За счет коэффициентов a и d матрицы преобразования происходит увеличение (или уменьшение) значения координат точки (x, y) в a и d раз по осям x и y соответственно:


В данном случае при s < 1 будет происходить увеличение значения координат точки (x, y) в s раз; при s > 1 мы получим обратный эффект — уменьшение значения координат (x, y) в s раз.

Здесь q — угол, на который требуется повернуть точку (x, y). Об этом говорит сайт https://intellect.icu . Обратите внимание: поворот происходит относительно точки (0, 0) декартовой системы координат против часовой стрелки!
А теперь вот вам маленькое задание. Попробуйте повернуть треугольник на угол q = 90o, координаты точек можете взять любые. Наш вариант представлен здесь.

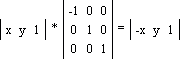

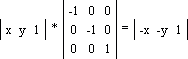

Чтобы провести любое сложное преобразование, необходимо разложить его на базовые операции. Поворот фигуры вокруг произвольной точки (m, n) на произвольный угол a состоит из трех базовых операций: 1) перенос фигуры на вектор A(-m, -n) для совмещения точки (m, n) с началом координат; 2) поворот фигуры на угол a; 3) перенос фигуры на вектор A'(m, n) для возвращения ее в исходное положение. Так как фигуру можно представить набором точек, то операции 1) - 3) можно выполнять последовательно для каждой точки. Покажем это на примере.
Пусть мы хотим повернуть треугольник с координатами A(x, y), B(x1, y1), C(x2, y2) вокруг точки D(m, n) на угол a. Пусть P-s — матрица переноса точки на вектор A(-m, -n), Va — матрица поворота на угол a, Ps — матрица переноса точки на вектор A'(m, n).
Итак, мы имеем все данные, необходимые для проведения сложного преобразования первой точки A(x, y):

Точно такие же преобразования необходимо провести для оставшихся двух точек треугольника, подставляя соответствующие их координаты взамен x и y (последовательность операций см. на рис. 1.7). Таким образом, сложная операция разбивается на простейшие и задается произведением соответствующих матриц преобразования, причем порядок, в котором перемножаются матрицы, существенно определяет результат.


px + qy + 1 = H — плоскость.
В общем случае от перемены матриц местами результат меняется.
Матрицы операций, идущие подряд, можно перемножать раздельно, главное — не менять их порядок следования (см. примечание 1).
Линии при описанных выше (аффинных) преобразованиях переходят в линии. Поэтому обычно производится пересчет только координат вершин фигуры, а после этого соответствующие вершины в результирующей фигуре соединяются, как и в исходной фигуре.
Пусть имеются две линии: x + y = 1, 2x - 3y = 0, необходимо найти точку их пересечения. Решение может быть найдено с использованием матриц. Перенесем все члены уравнений в левую часть: x + y - 1 = 0, 2x - 3y - 0 = 0; запишем коэффициенты первого уравнения в первый столбец матрицы, второго уравнения — во второй:

Условие, при котором пересекаются две прямые, выглядит следующим образом:
|x y 1| * M = |0 0 1|
Для нахождения ответа необходимо обе части предыдущего уравнения домножить справа на обратную матрицу M-1 (при перемножении M и M-1 получается единичная матрица E):
|x y 1| * E = |0 0 1| * M-1
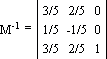
|x y 1| = |3/5 2/5 1|
Ответ: точка пересечения прямых: x = 3/5, y = 2/5.
Как задается точка знают все, а как задаются другие фигуры? Окружность задается тремя числами: x- и y-координатами центра и радиусом; для эллипса в дополнение к координатам центра нужно добавить величины двух его полуосей и еще направление одной из осей. Одну и ту же фигуру можно задать разными способами, но обычно выделяют те, для которых количество параметров является минимальным. Это минимальное количество называют «параметрическим числом образа». Составляя программы и алгоритмы машинной графики, надо знать параметрические числа основных геометрических образов.
| Таблица параметрических чисел для некоторых геометрических образов | ||
| Объект | Размерность пространства | Параметрическое число |
| Отрезок на плоскости | 2 | 4 |
| Отрезок в пространстве | 3 | 6 |
| Окружность в пространстве | 3 | 6 |
| Сфера | 3 | 4 |
| Дуга окружности на плоскости | 2 | 5 |
| Прямоугольник общего положения | 2 | 5 |
| Эллипс общего положения | 2 | 5 |
| Эллипсоид | 3 | 9 |
| Поверхность второго порядка | 3 | 9 |
| Линия полинома степени n | 2 | n+1 |
В задании объекта могут также участвовать «логические параметры». При этом можно ограничиться числами 0 и 1 или же устанавливать параметр по знаку числа. Эти параметры не влияют на параметрические числа объектов. Например, точка на окружности может быть задана значением одной из ее координат (X или Y), но надо будет указать, на какой полуокружности она может находиться.
В машинной графике существенно, с какого конца вычерчивается геометрический компонент, в этом случае должно задаваться направление вычерчивания. Это нужно для определения видимости сторон. Направление обхода тела можно задавать знаком «+» или «-», можно воспользоваться касательными, но чаще всего используются касательные векторы, или «векторы направления». Вектор на плоскости можно задать двумя его проекциями, касательные векторы имеют произвольную длину — поэтому можно ограничиться одним числом, однако из соображения удобства пользуются проекциями. На рис. 1.1a показана дуга, построенная по двум конечным точкам и проведенным их них касательным векторам. Этот набор (конечные точки и касательные векторы) — одна из типичных конфигураций данных. Если направление одного из векторов изменить на противоположное, то мы увидим картину, показанную на рис. 1.1b.

Таким образом, у линии можно будет выделить две области («стороны»): «положительную», с которой будут располагаться нормальные векторы, и «отрицательную». Линии, проведенные на поверхности, делят поверхность, а поверхности делят пространство. Данная методика применяется для решения задач нанесения штриховки на различные элементы чертежа, определения принадлежности точки телу сложной формы, выделения видимых или ограниченных частей и поверхностей.
Коснемся двух различных способов представления геометрических объектов в ЭВМ.
Первый способ — это аналитические модели. Аналитическая модель есть набор чисел и, если необходимо, логических параметров, которые играют роль коэффициентов и других величин в уравнениях, аналитических соотношениях, задающих объект данного типа. Например, для окружности основная форма аналитической модели — координаты центра и радиус, связанные известным соотношением: (x - xc)2 + (y - yc)2 - R2 = 0.
Окружность, как и многие другие объекты, может быть задана в параметрическом виде, где кроме координат есть еще одна переменная величина — параметр. Параметрическое задание образов широко применяется в компьютерной графике.
Второй способ численного моделирования геометрических объектов в ЭВМ — это координатные модели. В простых случаях — это наборы точек, которые принадлежат объектам и задаются координатами. Для кривых и ломанных линий точки располагаются в том же порядке, что и на линии. Упорядочить точки поверхности — более сложная задача: в большинстве случаев точки последовательно размещаются на линиях, проведенных на поверхности.
Координатные модели имеют несколько разновидностей:
Многие графические устройства имеют линейные интерполяторы. То есть если это устройсва траекторного типа, то элементы изображения представляются в виде координатных моделей, дополненых упраляющими командами. Последовательно задаваемые в них точки соединяются отрезками прямых, таким образом, все кривые представляются в виде ломанных с мелкими звеньями. Этот принцип позволяет заменять разнообразные и сложные в аналитическом отношении объекты на множества простых объектов. После этого с ними можно производить операции по одним и тем же алгоритмам. Для некоторых алгоритмов последовательные точки могут соединяться дугами каких-либо кривых, что позволяет снизить число опорных точек в модели, не уменьшая точности представления.
В общем, мой друг ты одолел чтение этой статьи об преобразования в двухмерном пространстве. Работы впереди у тебя будет много. Смело пиши комментарии, развивайся и счастье окажется в твоих руках. Надеюсь, что теперь ты понял что такое преобразования в двухмерном пространстве, компьютерная графика и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная графика
Комментарии
Оставить комментарий
Компьютерная графика
Термины: Компьютерная графика