Лекция 2 мин.
Привет, Вы узнаете о том , что такое метод оболочек, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое метод оболочек , настоятельно рекомендую прочитать все из категории Компьютерная графика.
метод оболочек получил широкое распространение в системах трехмерной машинной графики как для однопроцессорных, так и многопроцессорных машин. Свое название он получил от использования простых по конструкции трехмерных выпуклых фигур-оболочек, которые охватывают объект или его составные части и позволяют сравнительно просто выявлять часть пространства, где находится объект. Известно несколько модификаций метода, например показано его применение на этапе определения видимости.
Оболочки-многоугольники. Сущность метода, реализующего сокращение времени вычислений изображений с тенями, заключается в следующем. На этапе создания математической конструкции объекта каждый его отдельный элемент (примитив или система примитивов) окружается интерактивно или автоматически воображаемой оболочкой – выпуклым многогранником. Об этом говорит сайт https://intellect.icu . Число вершин и ориентация граней выбираются из соображений надежного охватывания тела элемента оболочкой, минимального объема оболочки и минимального числа граней.
При автоматическом построении выпуклой оболочки в качестве формы последней чаще всего выбирают параллелепипед. Основная идея определения положения и размеров параллелепипеда заключается в вычислении максимальных габаритных размеров охватывающего примитива вдоль осей. Так как отрезки, определяющие максимальные габаритные размеры, могут быть не параллельны осям, то часто построенная оболочка захватывает лишние, не принадлежащие объекту участки пространства, а это, в свою очередь, снижает эффективность метода. При "ручном" задании оболочки в виде неправильного многоугольника достигается более плотное облегание объекта, но зато требуется неавтоматизированная работа оператора. На практике эта работа сводится к выставлению в пространстве наименьшего числа точек, лежащих как можно ближе к объекту и одновременно таких, что выпуклая оболочка, построенная на этих точках, не сечет своими гранями объекта.
Кроме многогранников и параллелепипедов в качестве оболочек можно применить эллипсоиды. Замечательным свойством эллипсоида среди всех поверхностей второго порядка является замкнутость поверхности, и поэтому эллипсоид может быть использован как оболочка, охватывающая объект. Изменением размера и ориентации полуосей можно достаточно плотно охватить тело практически любой конфигурации.
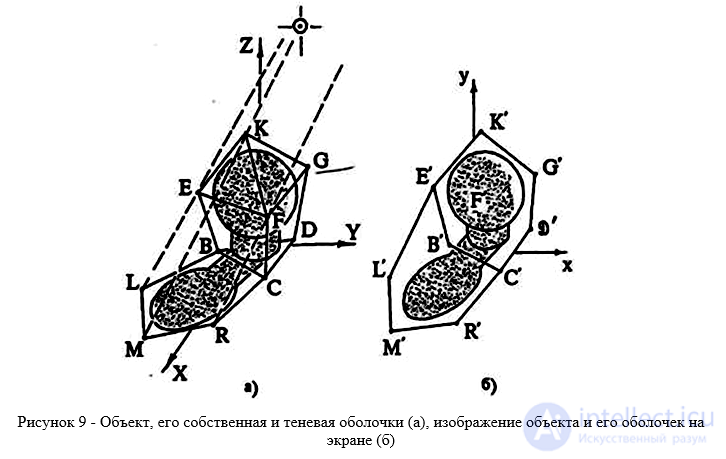
Рисунок 9 - Объект, его собственная и теневая оболочки (а), изображение объекта и его оболочек на экране (б)
Исследование, описанное в статье про метод оболочек, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое метод оболочек и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная графика
Из статьи мы узнали кратко, но содержательно про метод оболочек
Комментарии