2.3. Параметрические бикубические поверхности кратко

Привет, Вы узнаете о том , что такое параметрические бикубические поверхности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое параметрические бикубические поверхности , настоятельно рекомендую прочитать все из категории Компьютерная графика.

Перейдем теперь от кубических кривых к задаваемым бикубочным поверхностям.
кубическими уравнениями от двух переменных s и t. Изменяя оба параметра от 0 до 1 можно определить все точки на куске поверхности. Если один из параметров
присвоить постоянное значение, а другой изменять в диапазоне 0 – 1, то в результате получим кубическую кривую. Так же как и в случае кривых, мы будем рассматривать уравнение только для x:

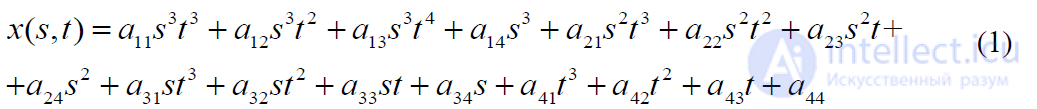
или в алгебраической форме:

где

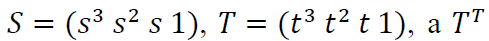
означает транспонируемую матрицу 𝑇.
𝐶𝑥 задает коэффициенты бикубического многочлена. Об этом говорит сайт https://intellect.icu . Существуют также 𝐶𝑦 и 𝐶𝑧 задающие
коэффициенты 𝑦(𝑠, 𝑡) и 𝑧(𝑠, 𝑡).

Чтобы записать поверхность в форме Эрмита применяется подход, аналогичный
изложенном для бикубических кривых, что позволяет использовать управляющие точки и касательные векторы для определения коэффициентов бикубического многочлена.
Рассмотрим уравнение бикубической кривой п 2.1(13), в котором t заменим на s.

Перепишем это уравнение так, чтобы геометрическая матрица Эрмита была не константой, а функцией t.

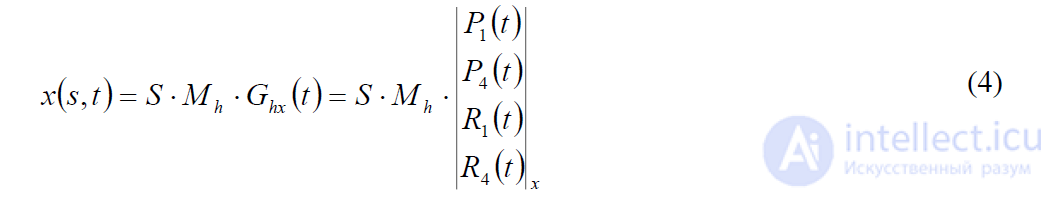
Функции P1x(t) и P4x(t) описывают x- компоненты начальной и конечной точек
кривой, задаваемой параметром s. Для каждого значения t определяются некоторые
две конечные точки. Аналогично R1x(t) и R4x(t) описывают касательные векторы в концевых векторах.
точках кубической кривой, построенной в зависимости от 𝑠.

Исследование, описанное в статье про параметрические бикубические поверхности, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое параметрические бикубические поверхности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная графика