3.3. Математическое описание плоских геометрических проекций кратко

Привет, Вы узнаете о том , что такое математика проекций, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое математика проекций , настоятельно рекомендую прочитать все из категории Компьютерная графика.

Для простоты будем считать, что при центральном проектировании центр проекции находится в начале координат, картинная плоскость перпендикулярна оси 𝑍 и совпадает с плоскостью 𝑧=𝑑, а при параллельном проектировании совпадает с плоскостью. Проекции рассматриваются в системе координат наблюдателя, которая является левосторонней. Система координат, в которой ось 𝑋 направлена ​​вправо, ось 𝑌 – вверх, а ось 𝑍 – вглубь экрана, естественно согласуется с экраном дисплея. Для перехода от правосторонней системы координат, в которой описывались преобразования переноса, поворота и масштабирования к левосторонней, в которой описаны проекции, можно воспользоваться матрицей

где координата 𝑧 умножается на −1
Каждую из проекций можно обрисовать матрицей 4×4. Это оказывается удобным, поскольку появляется возможность объединить матрицу проектирования с матрицей аффинных преобразований, представив в результате две операции преобразования (геометрический-перенос, масштабирование, поворот и проектирование) в виде одной матрицы.

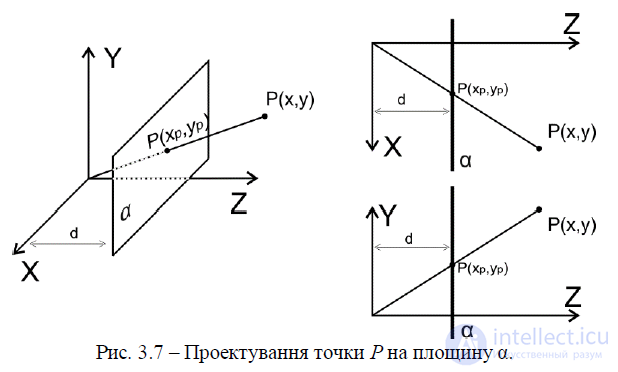
Рис. 3.7 – Проецирование точки P на плоскость α.

На рис. Об этом говорит сайт https://intellect.icu . 3.7 приведены три изображения в левосторонней системе координат, в которых точка Р проектируется на проекционную плоскость, расположенную на расстоянии от начала координат 𝑑.
Для вычисления координаты проекции точки (𝑥,𝑦,𝑧) напишем соотношения, полученные из подобных треугольников:

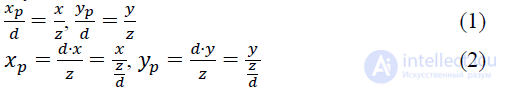
Расстояние 𝑑 является в данном случае масштабным множителем, применяемым к координатам 𝑥𝑝 и 𝑦𝑝. Причиной, приводящей к тому, что на центральной проекции более удаленные объекты выглядят мельче, чем ближние, является деление на 𝑧. Допустимы все значения 𝑧, за исключением 𝑧=0. Точки могут размещаться как позади центра проекции на отрицательной части оси 𝑍, так и между центром проекции и проекционной плоскостью.
Это преобразование можно представить в виде матрицы 4×4:

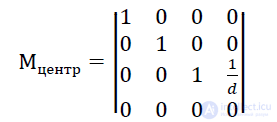
Умножая точку 𝑃 = |𝑥 𝑦 𝑧 1| на матрицу Мцентр, получим общее выражение для точки в однородных координатах |𝑋 𝑌 𝑍 𝑊|:

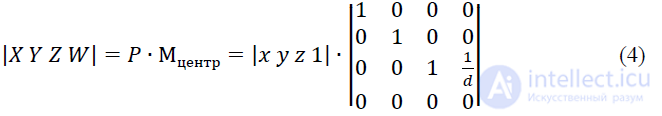
или

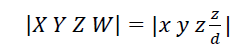(5)

Теперь, поделив на 𝑊 (которое равно 𝑧𝑑) для обратного перехода к трем измерениям, имеем

Этот результат является корректным, поскольку содержит преобразованную 𝑧- координату, что соответствует положению проекционной плоскости вдоль оси 𝑍.

Ортографическое проектирование на плоскость 𝑧 = 0 очевидно.

Направление проектирования совпадает с нормалью к плоскости проекции, то есть в нашем случае с осью 𝑍.
Таким образом, точка 𝑃 имеет координаты:

Эта проекция описывается матрицей

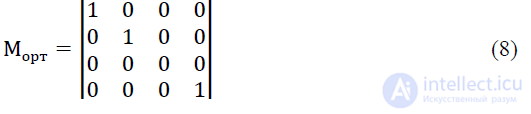
При косоугольной проекции, на плоскость XOY орт 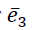= (0,0,1) переходит в = (𝑎, 𝑏, 0) т.е. направление проекции задается вектором

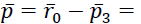(𝑎, 𝑏, −1)

Такое преобразование в однородных координатах можно задать с помощью матрицы.

В проекции кавале вектор 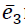переходит в (cos (𝜋⁄4), 𝑐𝑜𝑠 (𝜋 ⁄ 4),0),

а в проекции кабине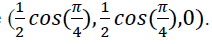

Исследование, описанное в статье про математика проекций, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое математика проекций и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная графика

Из статьи мы узнали кратко, но содержательно про математика проекций