Лекция
Привет, Вы узнаете о том , что такое треугольная сетка, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое треугольная сетка , настоятельно рекомендую прочитать все из категории Компьютерная графика.
В компьютерной графике треугольная сетка — это тип полигональной сетки . Она состоит из набора треугольников (обычно в трех измерениях ), соединенных общими ребрами или вершинами .
Многие графические программные пакеты и аппаратные устройства могут работать более эффективно с треугольниками, сгруппированными в сетки, чем с аналогичным количеством треугольников, представленных по отдельности. Это обычно происходит потому, что компьютерная графика выполняет операции с вершинами в углах треугольников. С отдельными треугольниками система должна работать с тремя вершинами для каждого треугольника. В большой сетке может быть восемь или более треугольников, встречающихся в одной вершине — обрабатывая эти вершины только один раз, можно выполнить часть работы и достичь идентичного эффекта.
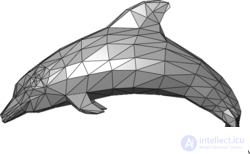
Пример треугольной сетки, представляющей дельфина
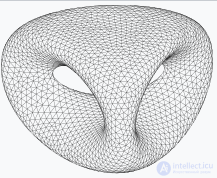
Треугольная сетка, созданная путем контурирования неявной поверхности
Во многих приложениях компьютерной графики необходимо управлять сеткой треугольников. Компонентами сетки являются вершины, ребра и треугольники. Приложению может потребоваться знание различных связей между компонентами сетки. Эти связи могут управляться независимо от фактических положений вершин. В этом документе описывается простая структура данных, которая удобна для управления связями. Это не единственная возможная структура данных. Существует много других типов, которые поддерживают различные запросы о сетках.
Возможны различные методы хранения и работы с сеткой в памяти компьютера. С API OpenGL и DirectX есть два основных способа передачи сетки треугольников графическому оборудованию: полосы треугольников и массивы индексов.
Одним из способов обмена данными вершин между треугольниками является полоса треугольников. В полосах треугольников каждый треугольник делит одно полное ребро с одним соседом, а другое — со следующим. Об этом говорит сайт https://intellect.icu . Другой способ — веер треугольников , который представляет собой набор соединенных треугольников, разделяющих одну центральную вершину. С помощью этих методов вершины обрабатываются эффективно, в результате чего требуется обрабатывать только N+2 вершины для рисования N треугольников.
Полосы треугольников эффективны, однако их недостатком является то, что может быть неочевидно, как или удобно преобразовывать произвольную сетку треугольников в полосы.
Структура данных, представляющая сетку, обеспечивает поддержку двух основных операций: вставки треугольников и удаления треугольников. Она также поддерживает операцию схлопывания ребер, которая полезна в схемах прореживания треугольников. Структура не обеспечивает поддержки позиций вершин, но предполагает, что каждой вершине назначен уникальный целочисленный идентификатор, обычно индекс этой вершины в массиве смежных позиций вершин. Вершина сетки определяется одним целым числом и обозначается hvi. Ребро сетки определяется парой целых чисел hv0,v1i, каждое целое число соответствует конечной точке ребра. Для поддержки карт ребер ребра хранятся так, что v0 = min(v0,v1). Компонент треугольника определяется тройкой целых чисел hv0,v1,v2i, каждое целое число соответствует вершине треугольника. Для поддержки карт треугольников треугольники хранятся так, что v0 = min(v0,v1,v2). Обратите внимание, что hv0,v1,v2i и hv0,v2,v1i рассматриваются как разные треугольники. Приложение, требующее двухсторонних треугольников, должно вставить обе тройки в структуру данных. Чтобы избежать постоянных напоминаний о порядке индексов, в оставшейся части документа информация о паре/тройке не подразумевает, что вершины упорядочены каким-либо образом (хотя реализация обрабатывает упорядочение).
Связность между компонентами полностью определяется набором троек, представляющих треугольники. Треугольник t = hv0,v1,v2i имеет вершины v0, v1 и v2. Он имеет ребра e0 = hv0,v1i, e1 = hv1,v2i и e2 = hv2,v0i. Обратные связи также известны. Вершина v0 смежна с ребрами e0 и e2 и треугольником t. Вершина v1 смежна с ребрами e0 и e1 и треугольником t. Вершина v2 смежна с ребрами e1 и e2 и треугольником t. Все три ребра e0, e1 и e2 смежны с t.
Сколько этой информации хранит структура данных, зависит от потребностей приложения. Более того, приложение может захотеть хранить дополнительную информацию в компонентах. Информация, хранящаяся в вершине, ребре или треугольнике, называется атрибутом вершины, атрибутом ребра или атрибутом треугольника. Абстрактные представления этих данных для простой структуры данных, описанной здесь,
Вершина = <целое число>; // v Край = <целое число, целое число>; // v0, v1 Треугольник <целое число,целое число,целое число>; // v0, v1, v2 VData = <данные вершин, специфичные для приложения>; EData = <данные периферии, специфичные для приложения>; TData = <данные треугольника, специфичные для приложения>; VAttribute = ,set>; // данные, eset, tset EAttribute = >; // данные, tset TAttribute = ; // данные VPair = pair<Вершина,VAttribute>; EPair = пара; TPair = pair<Треугольник,TAttribute>; VMap = карта; EMap = карта; TMap = карта; Сетка = ; // vmap, emap, tmap
Карты поддерживают стандартные функции вставки и удаления для хэш-таблицы. Вставка происходит только в том случае, если элемент еще не существует. Удаление происходит только в том случае, если элемент существует.
Эта операция включает в себя определение ребра hvk, vti, где vk называется вершиной сохранения, а vt называется вершиной выброса. Треугольники, которые разделяют это ребро, удаляются из сетки. Вершина vt также удаляется из сетки. Любые треугольники, которые разделяют vt, заменяют эту вершину на vk. На рисунке 1 показана сетка треугольников и последовательность из трех схлопываний ребер, примененных к сетке.
С индексными массивами сетка представлена двумя отдельными массивами, один массив содержит вершины, а другой содержит наборы из трех индексов в этом массиве, которые определяют треугольник. Графическая система сначала обрабатывает вершины, а затем визуализирует треугольники, используя наборы индексов, работающие с преобразованными данными. В OpenGL это поддерживается примитивом glDrawElements() при использовании Vertex Buffer Object (VBO).
С помощью этого метода любой произвольный набор треугольников, имеющих произвольное количество вершин, может быть сохранен, обработан и передан в графический API без какой-либо промежуточной обработки.
Исследование, описанное в статье про треугольная сетка, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое треугольная сетка и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная графика
Из статьи мы узнали кратко, но содержательно про треугольная сетка
Комментарии
Оставить комментарий
Компьютерная графика
Термины: Компьютерная графика