2.2.Параметрические бикубические кривые ПРЕДСТАВЛЕНИЕ ПРОСТРАНСТВЕННЫХ ФОРМ

Привет, Вы узнаете о том , что такое параметрические бикубические кривые, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое параметрические бикубические кривые , настоятельно рекомендую прочитать все из категории Компьютерная графика.

Основная цель – описать кривую с помощью последовательности сегментов кривой. Как правило, все векторные редакторы имеют схожий интерфейс редактирования кривых. Чтобы изменить форму кривой пользователь с помощью специального инструмента может изменять расположение узла и концы соприкасающихся с ним векторов. Чтобы кривая не имела изломов в точках соединения сегментов кривой, их соприкасающиеся векторы должны быть коллинеарны. (рис 2.1).

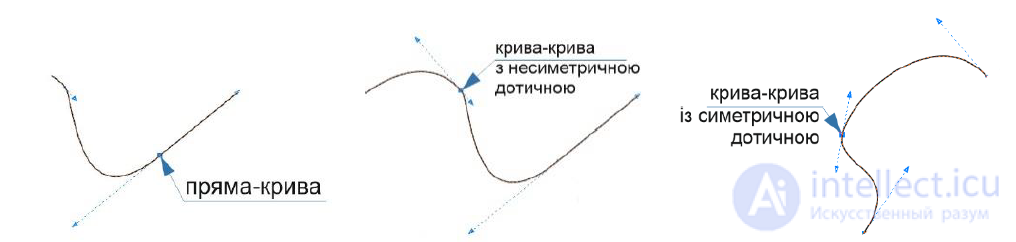
Рис. 2.1 – редактирование кривых в CorelDraw

Ниже для описания мы будем пользоваться общим обозначением 𝐶^(𝑖) -непрерывности. Говорят, что кривые 𝐶⁽⁰⁾ – непрерывны, если они не имеют разрывов, и кривые 𝐶⁽¹⁾ – непрерывны, если кроме того, непрерывны их соприкасающиеся (производные).
Существуют два основных способа представления кривых: с помощью функций переменных 𝑥, 𝑦, 𝑧 и функций некоторого параметра 𝑡.

В первом случае, чтобы определить точки (𝑥,𝑦,𝑧) на кривой, приходится иметь дело с функциями вида

𝑥=𝑥, 𝑦=𝑓(𝑥), 𝑧=𝑔(𝑥). (1)

Это представление влечет за собой много осложнений: в некоторой точке кривой тангенс угла наклона может оказаться равным бесконечности. Непроста также проверка, принадлежит ли точка некоторому сегменту кривой, заданному начальной и конечной точками.

При параметрическом представлении трехмерных кривых эти проблемы существенно упрощаются, поскольку при таком представлении легко описывать замкнутые.
многозначные функции и, кроме того, вместо тангенсов углов наклона используются соприкасающиеся векторы, никогда не бывают бесконечными.

Параметрической кубической кривой является кривая, в которой 𝑥, 𝑦, 𝑧 многочлены третьего порядка (кубические) относительно некоторого параметра 𝑡. Поскольку мы рассматриваем конечные отрезки кривой, то без потери общности можем ограничить диапазон изменения параметра и считать 0 ≤ 1.
Итак

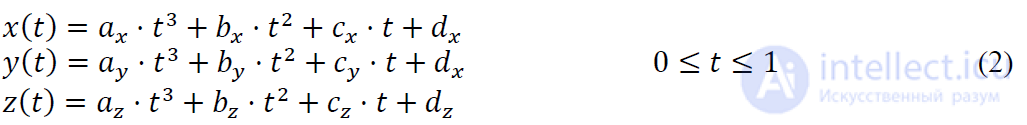
Производные функций 𝑥(𝑡), 𝑦(𝑡), 𝑧(𝑡) по параметру 𝑡 имеют один и тот же вид:

Три производных определяют касательный вектор. Тангенсы углов наклона кривой задаются как соотношение компонент этого вектора:

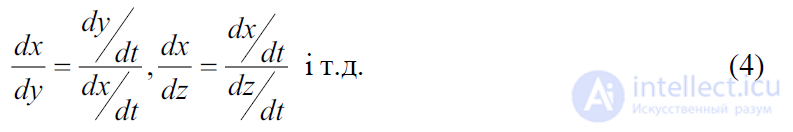
Углы наклона не зависят от длины соприкасающегося вектора. Если умножить производные на k, получим

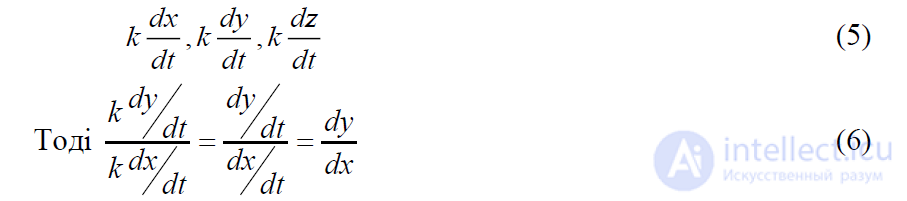
При поиске способов определения 𝑎𝑥, 𝑏𝑥, 𝑐𝑥, 𝑑𝑥 ниже мы будем иметь дело
только с производными 𝑥(𝑡). Для 𝑦(𝑡) и 𝑧(𝑡) производные и окончательные формулы аналогичны
формулам для 𝑥(𝑡) и мы их не будем приводить.

Почему мы рассматриваем именно кубические кривые? Потому что для сегментов кривой не
существует представление низшего порядка, которое обеспечивало бы в точке соединения
кривых друг с другом непрерывность положения и наклона сегментов и в то же время
гарантировало бы, что конечные точки сегмента кривой проходят через заданные точки.

Параметрический кубический многочлен с четырьмя коэффициентами является параметрической кривой наиболее низкой степени, при соответствующем выборе коэффициентов
может удовлетворять четырем условиям (положению каждого из концов сегмента и
касательным векторам в них).

Мы рассмотрим только три способа описания параметрических бикубических кривых:
метод Эрмита, в котором задаются положения конечных точек кривой и касаются
векторы в них; метод Безье, в котором задается положение конечных точек кривой,
а для неявной задачи соприкасающихся в этих точках используются две другие точки, обычно не лежащие на этой кривой; метод B-сплайнов, при котором конечные
точки не лежат на кривой, вследствие чего как первая, так и вторая производная оказываются непрерывными на концах сегмента. Об этом говорит сайт https://intellect.icu . (рис 4)

Рис. 2.2 – формы задания бикубических кривых: a – Эрмита; b – Безье, с – В-сплайн.

В форме Эрмита, задаются конечные точки и соприкасающиеся векторы к кривой в этих
точках (рис. 2.2-а) Зададим точки 𝑃1 и 𝑃4 и соприкасающиеся векторы 𝑅1 и 𝑅4 (точкам предоставляются индексы 1 и 4, а не 1 и 2 для совместимости с используемыми выражениями
при построении кривых методами Безье и В-сплайнов). Требуется найти коэффициенты 𝑎𝑥 , 𝑏𝑥 , 𝑐𝑥 , 𝑑𝑥 из выражения (2), удовлетворяющего условиям

Мы используем индекс x для ссылки на x-компоненты точек и соприкасающихся векторов. Переписывая выражение для x(t), получим.

где Т есть вектор-строка степеней 𝑡, а 𝐶𝑥 – вектор-столбец коэффициентов 𝑥(𝑡).
Запишем условия (7), используя уравнение (8).

Чтобы записать выражение для ограничений на соприкасающиеся векторы, продифференцируем
выражение (9) по 𝑡 и получим:

Выражения (9), (10) можно объединить в одно матричное уравнение

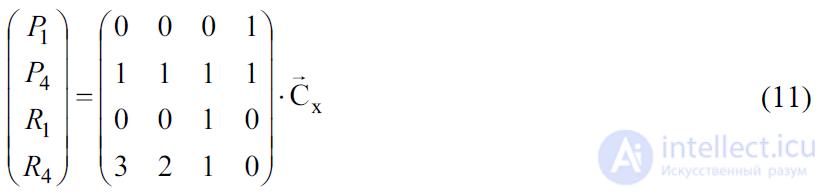
Найдя обратную матрицу, мы получим выражение для 𝐶𝑥 , если зададим:

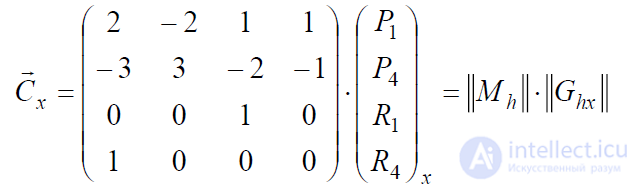
Через ‖𝑀ℎ‖ (𝑀ℎ) здесь обозначена эрмитовая матрица, а через ‖𝐺ℎ‖ (𝐺ℎ) геометрический вектор Эрмита.

Подставляя этот результат в (8), получим:

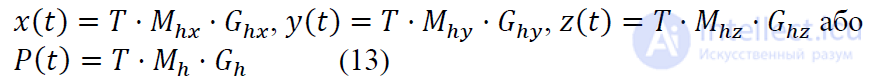
Если заданы 𝑃1, 𝑃4, 𝑅1, 𝑅4, можно определить 𝑥(𝑡), 𝑦(𝑡), 𝑧(𝑡) для 0 ≤ 𝑡 ≤ 1 и
найти все точки на сегменте кубической кривой от 𝑃1 до 𝑃4, у которого соприкасающийся вектор начальной точке равен 𝑅1, а в конечной – 𝑅4.

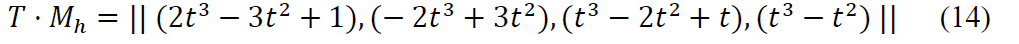
Умножив (14) на 𝐺ℎ𝑥, получим:

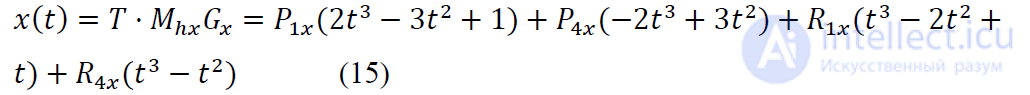
Четыре функции переменной 𝑡 в виде (15) называют функциями сопряжения,
поскольку с помощью двух первых соединяются точки 𝑃1 и 𝑃4, а с помощью
двух других – векторы 𝑅1 и 𝑅4, вследствие чего достигается "сглаженное" объединение
𝑥(𝑡).
Форма описания Безье очень близка к эрмитовой форме, но отличается заданием соприкасающихся векторов в конечных точках.
Соприкасающиеся векторы в конечных точках задаются отрезками [𝑃1𝑃2] и [𝑃3𝑃4].
В частности, касающиеся векторы эрмитовой формы 𝑅1 и 𝑅4 определялись таким образом, чтобы соответствовать четырем точкам Безье 𝑃1, 𝑃2, 𝑃3, 𝑃4:

Поэтому соотношение между эрмитовой матрицей и матрицей Безье Gb в общем случае записывается так:

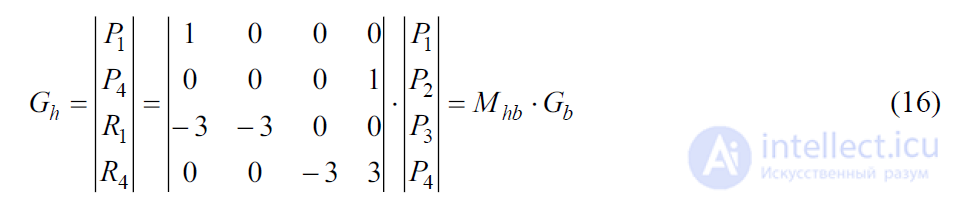
Подставляя (16) в (13), найдем: x(t)=T·Mh·Ghx = T·Mh·Mhb·Gbx
Обозначив через Mb произведение Mh·Mhb , получим выражение
x(t)=T·Mb·Gbx , имеющий теперь форму Безье. x(t)=T·Mb·Gbx

Непрерывность при сопряжении двух кривых Безъе обеспечивается соблюдением равенства векторов Р3Р4 = k Р4Р5.
Форма Безье благодаря своим двум свойствам используется в машинной.
графике чаще, чем эрмитовая форма. Во-первых, задавать (и изменять) касательные
векторы в форме двух точек в интерактивном режиме более удобно, чем в явном виде. Во-вторых четыре управляющие точки, определяющие выпуклый многоугольник
(выпуклую оболочку), внутри которой находится кривая Безье. Выпуклая оболочка оказывается полезной при отсечении кривой по окну или видимому объему.
Сплайном (spline) называли гибкую металлическую линейку — универсальное лекало,
которое использовали для того, чтобы гладко соединить отдельные точки на чертеже,
то есть для графической интерполяции. Более того, кривая, описывающая деформацию
гибкой линейки, зафиксированной в отдельных точках, является сплайном. Таким образом гибкая
линейка является физической моделью сплайн-функции (или, напротив, сплайн-функция является математической моделью гибкой линейки).

B-сплайн (базисный сплайн) – сплайн-функция, имеющая минимальный носитель для
заданной степени, порядка гладкости и области определения.
Фундаментальная теорема утверждает, что произвольная сплайн-функция заданного
степени, гладкости и области определения может быть представлена ​​как линейная комбинация B-сплайнов той же степени и гладкости на той же области определения.
Кривая, представленная в виде кубического В-сплайна, в общем случае
может проходить через любые управляющие точки, однако она непрерывна и, кроме
того, непрерывны ее соприкасающийся вектор и кривизна (т.е. первая и вторая производные кривой непрерывны в конечных точках) в отличии от форм Эрмита и Безье, у которых в
конечных точках непрерывны только первые производные, проходящие через управляющие точки. Таким образом, можно утверждать, что форма В-сплайнов более "гладкая", чем другие формы. Термин сплайн происходит от названия длинных гибких металлических линеек, с помощью которых чертежи размечали поверхности самолетов и кораблей.

Металлический сплайн, если не сильно напряжен, также имеет непрерывность второго порядка. В-сплайн описывается следующей формулой:

При аппроксимации управляющих точек Р1, Р2,...Рn последовательностью В-сплайнов
мы будем применять между каждой парой соседних точек геометрические матрицы. Для аппроксимации в интервале, близком к точкам Pi и Pi+1, (рис. 2.2-с) используется

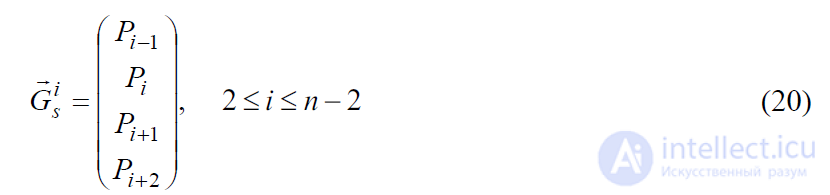
Свойство выпуклой оболочки кривой Безье также справедливо для кривых в форме В-сплайнов: выпуклая оболочка кривой в приближенном интервале Pi - Pi+1
та же, что и для четырех управляющих точек, используемых для генерации кривой: Pi - 1, Pi, Pi+1, Pi+2

Форма Эрмита пригодна для аппроксимации уже имеющихся поверхностей, когда необходимо добиться как соответствия точек, так и соответствия векторов, тогда как представление в виде В-сплайнов удобно для аппроксимации точек и достижения.
C(2)-непрерывности. Формы Безье и В-сплайн пригодны для работы в интерактивном режиме.
Обе эти формы обладают свойством выпуклой оболочки. Отметим,
что кривую, первоначально заданную в одной форме, можно превратить в другую форму, если записать геометрический вектор первой формы в терминах второй.

Исследование, описанное в статье про параметрические бикубические кривые, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое параметрические бикубические кривые и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная графика