Проекции трехмерных объектов на двухмерной проекционной плоскости кратко

Привет, Вы узнаете о том , что такое проекции объектов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое проекции объектов , настоятельно рекомендую прочитать все из категории Компьютерная графика.

Несоответствие между пространственными объектами и плоскими изображениями устраняет проектирование создания проекции трехмерных объектов на двухмерной проекционной плоскости. Проекция трехмерного объекта, представленного в виде совокупности точек, строится с помощью прямых проектирующих лучей, которые называются проекторами и выходят из центра проекции, проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию. (рис.3.2)

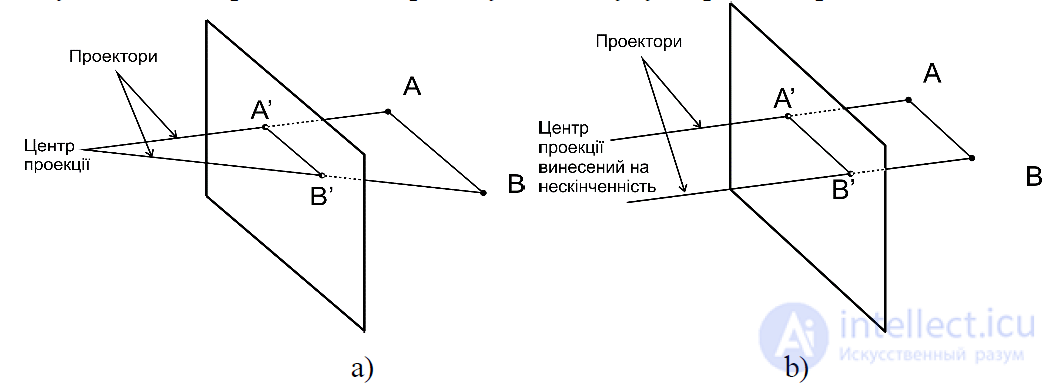
Рис. 3.2 – Отрезок АВ и его проекция A'B': a – центральная; b – параллельно.
Поскольку проекция отрезка сама является отрезком, достаточно спроектировать только конечные точки. Определенный таким образом класс проекций известен под названием плоских геометрических проекций, поскольку проектирование в этом случае производится на плоскость, а не на искривленную поверхность, и в качестве проекторов берутся прямые, а не кривые линии. В отличии от них многие картографические проекции являются либо неплоскими, либо негеометрическими.

Плоские геометрические проекции, которые в дальнейшем будем называть просто проекциями, можно подразделить на два основных класса: центральные и параллельные. Различие между ними определяется соотношением между центром проекции и проекционной плоскостью. Если расстояние между ними конечно, то проекция будет центральной, если же бесконечна, то проекция будет параллельной. При описании центральной проекции мы явно задаем ее центр проекции, в то время как определяя параллельную проекции, мы указываем направление проектирования.

Центральная проекция порождает визуальный эффект, аналогичный тому, к которому приводят фотографические системы или зрительная система человека, и поэтому используется в случае, когда требуется достичь определенной степени реальности. Этот эффект известен как перспективное укорочение: размер центральной проекции объекта уменьшается с приближением проекционной плоскости к центру проекции. Это означает, что, хотя центральная проекция реалистична, она оказывается непригодной для представления точной формы и размеров объекта: из проекции нельзя получить информацию о расстояниях; углы хранятся только на тех гранях объекта, которые параллельны проекционной плоскости; проекции параллельных линий в общем случае не параллельны.

Параллельная проекция порождает менее реалистичное изображение, поскольку отсутствует перспективное укорочение, хотя при этом могут иметь место разные постоянные укорочения вдоль каждой из осей. Об этом говорит сайт https://intellect.icu . Проекция фиксирует истинные размеры (с точностью до скалярного множителя), и параллельные прямые остаются параллельными. Как и в случае центральной проекции, углы сохраняются только на тех гранях объекта, которые параллельны проекционной плоскости.

Центральные проекции любой совокупности параллельных прямых, не параллельные проекционной плоскости будут сходиться в точке восхождения. Существует нескончаемое число точек схождения. Если совокупность прямых параллельна одной из главных координатных осей, то их точка восхождения называется главной точкой восхождения. Есть только три такие точки, соответствующие трем координатным осям. Если, например, проекционная плоскость пересекает одну только ось 𝑧 и, следовательно, перпендикулярна ей, то только на этой оси будет лежать главная точка схождения, поскольку прямые, параллельные как 𝑦 -, так и 𝑥 - осям, параллельны также и проекционной плоскости и поэтому нет точки восхождения.

Центральные проекции классифицируются в зависимости от числа главных точек схождения, которые они имеют, а следовательно, и от числа координатных осей, пересекаемых проекционной плоскостью.

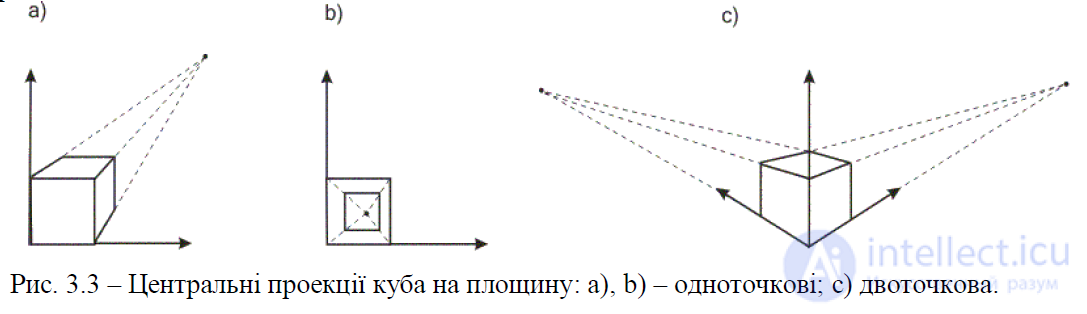
Рис. 3.3 – Центральные проекции куба на плоскость: a), b) – одноточечные; с) двухточечная.

Двухточечная центральная проекция широко применяется в проектировании и в рекламных изображениях, в которых вертикальные прямые проектируются как параллельные и, следовательно, не сходятся. Трехточечные центральные проекции почти совсем не используются, во-первых, потому, что их трудно строить, а во-вторых, из-за того, что они придают мало нового с точки зрения реалистичности по сравнению с двухточечной проекцией.
Параллельные проекции разделяются на два типа в зависимости от соотношения между направлением проектирования и нормалью к проекционной плоскости. в ортографических параллельных проекциях эти направления совпадают, а в косоугольных параллельных проекциях они не совпадают. То есть в ортографических проекциях направление проектирования является нормалью к проекционной плоскости.

Наиболее распространенными видами ортографических проекций являются вид спереди, вид сверху (план) и вид сбоку (рис. 3.4), в которых картинная плоскость перпендикулярна главным координатным осям, совпадающим вследствие этого с направлением проектирования. По этим проекциям можно измерять расстояния и углы.

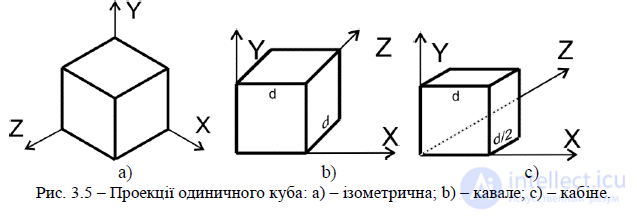
Рис. 3.5 – Проекции единичного куба: a) – изометрическая; b) – кавалье ; c) – кабине.

Рис. 3.4 – Ортографические проекции усеченного куба

При аксонометрических ортографических проекциях используются проекционные плоскости, не перпендикулярные главным координатным осям, поэтому на них изображаются сразу несколько сторон объекта, равно как и при центральном проектировании. Однако в аксонометрии укорочение постоянно, тогда как для центральной проекции оно связано с расстоянием от центра проекции. При аксонометрическом проектировании сохраняется параллельность прямых, а углы изменяются; расстояния можно измерять вдоль главных координатных осей (в общем случае, с разными масштабными коэффициентами).

Часто используемая аксонометрическая проекция представляет собой изометрическую проекцию (рис.3.5-а). В этом случае нормаль к проекционной плоскости (а следовательно и направление проектирования) составляет равные углы с каждой из главных координатных осей. Изометрическая проекция обладает следующим свойством: все три главные координатные оси одинаково укорачиваются. Поэтому можно производить измерения вдоль направления осей с одним тем же масштабом (отсюда название ИЗО равно).
Косоугольные проекции. Проекционная плоскость перпендикулярна главной координатной оси. Сторона объекта, параллельная этой плоскости, проектируется так, что можно измерять углы и расстояния. Проектирование других сторон также допускает проведение линейных (но не угловых) измерений вдоль главных осей.

Двумя важными видами косоугольных проекций являются проекции кавале (рис. 3.5-b) – cavalier (в отечественной литературе горизонтальная косоугольная изометрия – военная перспектива) и кабине (рис. 3.5-c) – cabinet (фронтальная косоугольная диметрия – кабинетная проекция).
В проекции кузнец направление проектирования, как правило, составляет с проекционной плоскостью угол 45°. Расстояния по каждой оси откладываются одинаково, что позволяет производить измерения, но искажает представление о реальной форме объекта.
Проекция кабине имеет направление проектирования, которое составляет с проекционной плоскостью угол 𝑎𝑟𝑐𝑐𝑡𝑔(1/2). При этом отрезки, перпендикулярные проекционной плоскости, после проектирования составляют половину их действительной длины. Проекции кабины более реалистичны, чем проекции кавале, поскольку укорочение с коэффициентом 1/2 больше согласуется с нашим визуальным опытом.

Исследование, описанное в статье про проекции объектов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое проекции объектов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная графика

Из статьи мы узнали кратко, но содержательно про проекции объектов