Графические и геометрические примитивы в компьютерной графике

Привет, Вы узнаете о том , что такое геометрические примитивы, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое геометрические примитивы , настоятельно рекомендую прочитать все из категории Компьютерная графика.

В векторной компьютерной графике , системах автоматизированного проектирования и географических информационных системах геометрический примитив (или прим ) — это простейшая (т. е. «атомарная» или неприводимая) геометрическая форма , которую система может обрабатывать (рисовать, хранить). Иногда подпрограммы , которые рисуют соответствующие объекты, также называют «геометрическими примитивами». Наиболее «примитивными» примитивами являются точка и отрезок прямой линии , которые были всем, что было в ранних системах векторной графики.

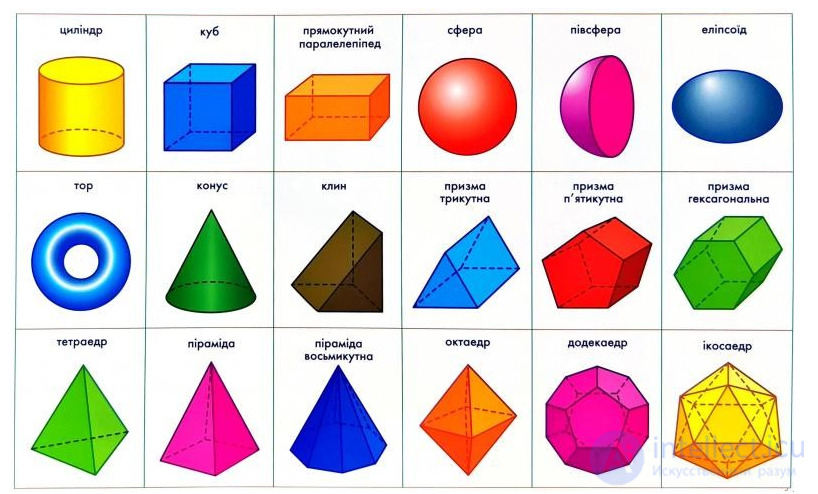
В конструкционной блочной геометрии (стереометрии)примитивами называют простые геометрические тела такие как куб , цилиндр , сфера , конус , пирамида , тор .

Современные компьютерные системы 2D-графики могут оперировать такими примитивами как линии (отрезки прямых линий, кругов или более сложных кривых, таких как кривые Безье ), а также формами (треугольники, прямоугольники, произвольные многоугольники, круги).

Обычный набор двумерных примитивов включает линии, точки и многоугольники , хотя некоторые люди предпочитают считать треугольники примитивами, потому что каждый многоугольник может быть построен из треугольников. Все остальные графические элементы построены из этих примитивов. В трех измерениях треугольники или многоугольники, расположенные в трехмерном пространстве, могут использоваться в качестве примитивов для моделирования более сложных трехмерных форм. В некоторых случаях примитивами могут считаться кривые (такие как кривые Безье , окружности и т. д.); в других случаях кривые представляют собой сложные формы, созданные из множества прямых примитивных форм.

Обычные (Общие) примитивы

3D тор

• точка
• прямая или отрезок
• плоскость
• круг или эллипс
• треугольник , четырехугольник или произвольный полигон
• сплайн

В 3D-приложениях базовые геометрические фигуры и формы отличаются от приведенных выше. Среди них:

• сфера
• куб или прямоугольный параллелепипед
• тор
• цилиндр
• пирамида
• сетку из треугольников или полигональную сетку которые состоят из связанных вершин

3D-приложения могут иметь расширенный список примитивов, имеющих более сложные формы, идущие вместе с приложением. К примеру, чайник является примитивом в 3D Studio Max .

Набор геометрических примитивов основан на размерности представляемой области:

• Точка (0-мерная), отдельное место без высоты, ширины или глубины.
• Линия или кривая (одномерная), имеющая длину, но не имеющая ширины, хотя линейный объект может изгибаться в пространстве более высокой размерности.
• Плоская поверхность или криволинейная поверхность (двумерная), имеющая длину и ширину.
• Объемная область или тело (трехмерное), имеющее длину, ширину и глубину.

В ГИС поверхность рельефа часто в разговорной речи называют «2 1/2-мерной», поскольку необходимо представить только верхнюю поверхность. Таким образом, высоту можно концептуализировать как свойство скалярного поля или функцию двумерного пространства, что дает ей ряд эффективностей моделирования данных по сравнению с настоящими трехмерными объектами. Форма любого из этих измерений, больших нуля, состоит из бесконечного числа отдельных точек. Поскольку цифровые системы конечны, можно сохранить только выборочный набор точек в форме. Таким образом, векторные структуры данных обычно представляют геометрические примитивы с использованием стратегической выборки, организованной в структуры, которые облегчают программному обеспечению интерполяцию оставшейся части формы во время анализа или отображения с использованием алгоритмов вычислительной геометрии .

• Точка — это отдельная координата в декартовой системе координат . Некоторые модели данных допускают многоточечные объекты, состоящие из нескольких разъединенных точек.

Простая полилиния

• Полигональная цепь или полилиния — это упорядоченный список точек (в данном контексте называемых вершинами ). Ожидается, что программное обеспечение будет интерполировать промежуточную форму линии между соседними точками в списке как параметрическую кривую, чаще всего прямую линию, но часто доступны и другие типы кривых, включая дуги окружности , кубические сплайны и кривые Безье . Некоторые из этих кривых требуют определения дополнительных точек, которые не находятся на самой линии, но используются для параметрического управления.
• Полигон — это полилиния, которая замыкается в своих конечных точках, представляя границу двумерной области. Ожидается, что программное обеспечение будет использовать эту границу для разделения двумерного пространства на внутреннюю и внешнюю части. Некоторые модели данных допускают, чтобы один объект состоял из нескольких полилиний, которые могут совместно соединяться, образуя единую замкнутую границу, могут представлять набор непересекающихся областей (например, штат Гавайи ) или могут представлять область с отверстиями (например, озеро с островом).
• Трехмерный торический прим, созданный в Second Life , пример параметрической формы
• 

• Параметрическая фигура — это стандартизированная двумерная или трехмерная фигура, определяемая минимальным набором параметров, например, эллипс , определяемый двумя точками в фокусах или тремя точками в центре, вершине и совершине.
• Многогранник или сетка полигона — это набор граней полигона в трехмерном пространстве, которые соединены по краям, чтобы полностью заключить объемную область. Об этом говорит сайт https://intellect.icu . В некоторых приложениях замыкание может не требоваться или может подразумеваться, например, при моделировании рельефа. Ожидается, что программное обеспечение будет использовать эту поверхность для разделения трехмерного пространства на внутреннюю и внешнюю части. Сетка треугольника — это подтип многогранника, в котором все грани должны быть треугольниками, единственный многоугольник, который всегда будет плоским, включая триангулированную нерегулярную сеть (TIN), обычно используемую в ГИС.

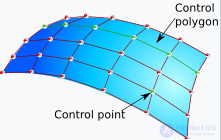
Поверхность NURBS

• Параметрическая сетка представляет собой трехмерную поверхность, созданную с помощью связанного набора параметрических функций, подобно сплайну или кривой Безье в двух измерениях. Наиболее распространенной структурой является неравномерный рациональный B-сплайн (NURBS), поддерживаемый большинством САПР и программного обеспечения для анимации.

В графических процессорах используются аппаратные ускорения для рендеринга таких примитивов как точки и треугольники, обычно с текстурами и шейдерами .

Текстура ( англ. Texture mapping ) — это способ придания поверхности 3D детали — полигона : цвета, фактуры, блеска, матовости и других физических свойств (для имитации чаще всего какого-либо природного материала, например бумаги, дерева, камня, металла и т.п.).

Шейдер ( англ. Shader ) — программа для одной из степеней графического конвейера, используемая в трехмерной графике для определения окончательных параметров объекта или изображения. Она может включать в себя произвольной сложности описание поглощения и рассеяния света, наложение текстуры, отражение и преломление, затенение, смещение поверхности и эффекты постобработки.

Программируемые шейдеры гибкие и эффективные. Сложные с виду поверхности могут быть визуализированы с помощью простых геометрических форм. К примеру, шейдеры могут быть использованы для рисования поверхности из трехмерной керамической плитки на абсолютно плоской поверхности.

Современные 3D-ускорители обычно принимают набора треугольников в виде полосы треугольников .

Ранние векторные форматы, такие как POLYVRT , ARC/INFO Coverage и шейп-файл Esri , поддерживают базовый набор геометрических примитивов: точки, полилинии и полигоны, только в двумерном пространстве, а последние два — только с интерполяцией прямых линий. Также были добавлены структуры данных TIN для представления поверхностей рельефа в виде треугольных сеток. С середины 1990-х годов были разработаны новые форматы, расширяющие диапазон доступных примитивов, в целом стандартизированных спецификацией Simple Features Открытого геопространственного консорциума . Распространенные расширения геометрических примитивов включают: трехмерные координаты для точек, линий и полигонов; четвертое «измерение» для представления измеренного атрибута или времени; изогнутые сегменты в линиях и полигонах; текстовая аннотация как форма геометрии; и полигональные сетки для трехмерных объектов.

Часто представление формы явления реального мира может иметь иное (обычно меньшее) измерение, чем представляемое явление. Например, город (двумерный регион) может быть представлен в виде точки, а дорога (трехмерный объем материала) может быть представлена ​​в виде линии. Это размерное обобщение коррелирует с тенденциями в пространственном познании. Например, вопрос о расстоянии между двумя городами предполагает концептуальную модель городов как точек, в то время как указание направлений, включающих движение «вверх», «вниз» или «вдоль» дороги, подразумевает одномерную концептуальную модель. Это часто делается в целях эффективности данных, визуальной простоты или когнитивной эффективности и приемлемо, если различие между представлением и представляемым понятно, но может вызвать путаницу, если пользователи информации предполагают, что цифровая форма является идеальным представлением реальности (т. е. верят, что дороги на самом деле являются линиями).

В программном обеспечении САПР или 3D-моделировании интерфейс может предоставлять пользователю возможность создавать примитивы, которые могут быть дополнительно изменены путем редактирования. Например, в практике моделирования коробок пользователь начнет с кубоида, затем использует выдавливание и другие операции для создания модели. В этом использовании примитив является просто удобной отправной точкой, а не фундаментальной единицей моделирования.

Пакет 3D может также включать список расширенных примитивов, которые являются более сложными формами, входящими в пакет. Например, чайник указан как примитив в 3D Studio Max .

• Скульптурная чопорность
• Симплекс

Исследование, описанное в статье про геометрические примитивы, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое геометрические примитивы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная графика