Лекция
Сразу хочу сказать, что здесь никакой воды про система кодирования информации, и только нужная информация. Для того чтобы лучше понимать что такое система кодирования информации, бит, байт, трит, трайт, кубит , настоятельно рекомендую прочитать все из категории Информатика.
Кодирование информации применяют для унификации формы представления данных, которые относятся кразличным типам, в целях автоматизации работы с информацией.
Кодирование – это выражение данных одного типа через данные другого типа. Например, естественные человеческие языки можно рассматривать как системы кодирования понятий для выражения мыслей посредством речи, к тому же и азбуки представляют собой системы кодирования компонентов языка с помощью графических символов.
В вычислительной технике применяется двоичное кодирование. Основой этой системы кодирования является представление данных через последовательность двух знаков: 0 и 1. Данные знаки называются двоичными цифрами (binary digit), или сокращенно bit ( бит ). Одним битом могут быть закодированы два понятия: 0 или 1 (да или нет, истина или ложь и т. п.). Двумя битами возможно выразить четыре различных понятия, а тремя – закодировать восемь различных значений.
Наименьшая единица кодирования информации в вычислительной технике после бита – байт . Его связь с битом отражает следующее отношение: 1 байт = 8 бит = 1 символ.
Обычно одним байтом кодируется один символ текстовой информации. Исходя из этого для текстовых документов размер в байтах соответствует лексическому объему в символах.
Более крупной единицей кодирования информации служит килобайт, связанный с байтом следующим соотношением: 1 Кб = 1024 байт.
Другими, более крупными, единицами кодирования информации являются символы, полученные с помощью добавления префиксов мега (Мб), гига (Гб), тера (Тб):
1 Мб = 1 048 580 байт;
1 Гб = 10 737 740 000 байт;
1 Тб = 1024 Гб.
Для кодирования двоичным кодом целого числа следует взять целое число и делить его пополам до тех пор, пока частное не будет равно единице. Совокупность остатков от каждого деления, которая записывается справа налево вместе с последним частным, и будет являться двоичным аналогом десятичного числа.
В процессе кодирования целых чисел от 0 до 255 достаточно использовать 8 разрядов двоичного кода (8 бит). Применение 16 бит позволяет закодировать целые числа от 0 до 65 535, а с помощью 24 бит – более 16,5 млн различных значений.
Для того чтобы закодировать действительные числа, применяют 80-разрядное кодирование. В этом случае число предварительно преобразовывают в нормализованную форму, например:
2,1427926 = 0,21427926 ? 101;
500 000 = 0,5 ? 106.
Первая часть закодированного числа носит название мантиссы, а вторая часть – характеристики. Основная часть из 80 бит отводится для хранения мантиссы, и некоторое фиксированное число разрядов отводится для хранения характеристики.
Байт (англ. byte) — единица хранения и обработки цифровой информации; совокупность битов, обрабатываемая компьютером одномоментно. В современных вычислительных системах байт состоит из восьми битов и, соответственно, может принимать одно из 256 (28) различных значений (состояний, кодов). Однако в истории компьютерной техники существовали решения с иными размерами байта (например, 6, 32 или 36 битов), поэтому иногда в компьютерных стандартах и официальных документах для однозначного обозначения группы из 8 битов используется термин «октет» (лат. octet).
В большинстве вычислительных архитектур байт — это минимальный независимо адресуемый набор данных.
Название «байт» (слово byte представляет собой сокращение словосочетания BinarY TErm — «двоичный терм» ) было впервые использовано в 1956 году В. Бухгольцем (англ. Werner Buchholz) при проектировании первогосуперкомпьютера IBM 7030 Stretch для пучка одновременно передаваемых в устройствах ввода-вывода шести битов. Позже, в рамках того же проекта, байт был расширен до восьми бит.
Ряд ЭВМ 1950-х и 1960-х годов (БЭСМ-6, М-220) использовали 6-битовые символы в 48-битовых или 60-битовых машинных словах. В некоторых моделях ЭВМ производства Burroughs Corporation (ныне Unisys) размер символа был равен 9 битам. Всоветской ЭВМ Минск-32 использовался 7-битный байт.
Байтовая адресация памяти была впервые применена в системе IBM System/360. В более ранних компьютерах адресовать можно было только целиком машинное слово, состоявшее из нескольких байтов, что затрудняло обработку текстовых данных.
8-битные байты были приняты в System/360, вероятно, из-за использования BCD-формата представления чисел: одна десятичная цифра (0-9) требует 4 бита (тетраду) для хранения; один 8-битный байт может представлять две десятичные цифры. 6-битные байты могут хранить только по одной десятичной цифре, два бита остаются незадействованными.
По другой версии, 8-битный размер байта связан с 8-битным же числовым представлением символов в кодировке EBCDIC.
По третьей версии, из-за двоичной системы кодирования в компьютерах наиболее выгодными для аппаратной реализации и удобными для обработки данных являются длины слов кратные степеням 2, в том числе и 1 байт = 23 = 8 битов, системы и компьютеры с длинами слов не кратными числу 2 отпали из-за невыгодности и неудобства.
Постепенно 8-битные байты стали стандартом де-факто; с начала 1970-х в большинстве компьютеров байты состоят из 8 бит, а размер машинного слова кратен 8 битам.
Из соображений удобства единицы нетекстовых типов данных также делают кратными восьми битам, например:
Количество состояний (кодов, значений), которое может принимать 1 восьмибитный байт с позиционным кодированием, определяется в комбинаторике, равно количеству размещений с повторениями и вычисляется по формуле:
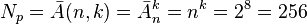 возможных состояний (кодов, значений), где
возможных состояний (кодов, значений), где
 — количество состояний (кодов, значений) в одном байте.
— количество состояний (кодов, значений) в одном байте.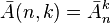 — количество размещений с повторениями.
— количество размещений с повторениями.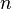 — количество состояний (кодов, значений) в одном бите; в бите 2 состояния (n=2).
— количество состояний (кодов, значений) в одном бите; в бите 2 состояния (n=2).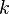 — количество битов в байте; в 8-битном байте k=8 и в нем может быть от 0 до 8 одинаковых битов (повторений).
— количество битов в байте; в 8-битном байте k=8 и в нем может быть от 0 до 8 одинаковых битов (повторений).| Измерения в байтах | ||||||||
|---|---|---|---|---|---|---|---|---|
| ГОСТ 8.417-2002 | Приставки СИ | приставки МЭК | ||||||
| Название | Символ | Степень | Название | Степень | Название | Символ | Степень | |
| байт | Б | 100 | - | 100 | байт | B | Б | 20 |
| килобайт | кБ | 103 | кило- | 103 | кибибайт | KiB | КиБ | 210 |
| мегабайт | МБ | 106 | мега- | 106 | мебибайт | MiB | МиБ | 220 |
| гигабайт | ГБ | 109 | гига- | 109 | гибибайт | GiB | ГиБ | 230 |
| терабайт | ТБ | 1012 | тера- | 1012 | тебибайт | TiB | ТиБ | 240 |
| петабайт | ПБ | 1015 | пета- | 1015 | пебибайт | PiB | ПиБ | 250 |
| эксабайт | ЭБ | 1018 | экса- | 1018 | эксбибайт | EiB | ЭиБ | 260 |
| зеттабайт | ЗБ | 1021 | зетта- | 1021 | зебибайт | ZiB | ЗиБ | 270 |
| йоттабайт | ЙБ | 1024 | йотта- | 1024 | йобибайт | YiB | ЙиБ | 280 |
Кратные приставки для образования производных единиц для байта применяются не как обычно: уменьшительные приставки не используются совсем, а единицы измерения информации, меньшие, чем байт, называются специальными словами (ниббл и бит); увеличительные приставки кратны 1024=210, то есть 1 килобайт равен 1024 байтам, 1 мегабайт — 1024 килобайтам или 1 048 576 байтам и т. д. для гиби-, тера- и пебибайтов. Разница между емкостями (объемами), выраженными в кило = 103 = 1000 и выраженными в киби = 210 = 1024, возрастает с ростом веса приставки. МЭК рекомендует использовать двоичные приставки, но на практике они пока не применяются, возможно, из-за неблагозвучности — кибибайт, мебибайт, йобибайт и т. п.
Иногда десятичные приставки используются и в прямом смысле, например, при указании емкости жестких дисков: у них гигабайт может обозначать не 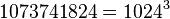 байтов, а миллион килобайтов (то есть 1 024 000 000 байтов), а то и просто миллиард байтов.
байтов, а миллион килобайтов (то есть 1 024 000 000 байтов), а то и просто миллиард байтов.
Межгосударственный (СНГ) стандарт ГОСТ 8.417-2002 («Единицы величин») в «Приложении А» для обозначения байта регламентирует использование русской прописной буквы «Б». Кроме того, констатируется традиция использования приставок СИ вместе с наименованием «байт» для указания множителей, являющихся степенями двойки (1 Кбайт = 1024 байт, 1 Мбайт = 1024 Кбайт, 1 Гбайт = 1024 Мбайт и т. д., причем вместо строчной «к» используется прописная «К»), и упоминается, что подобное использование приставок СИ не является корректным.
Использование прописной буквы «Б» для обозначения байта соответствует требованиям ГОСТ и позволяет избежать путаницы между сокращениями от байт и бит. Однако следует учитывать, что в стандарте нет сокращения для «бит», поэтому использование записи вроде «Гб» как синонима для «Гбит» недопустимо.
В международном стандарте МЭК IEC 60027-2 2005 года , для применения в электротехнической и электронной областях, рекомендуются обозначения:
Согласно рекомендации Института русского языка имени В. В. Виноградова Российской Академии Наук байт, как и бит, склонять необходимо .
Кроме обычной формы родительного падежа (битов, байтов, килобайтов) существует счетная форма, которая используется в сочетании с числительными: 8 байт, 16 килобайт. Счетная форма является разговорной. Точно так же, например, с килограммами: обычная форма родительного падежа употребляется, если нет числительного, а в сочетании с числительным могут быть варианты: 16 килограммов (стилистически нейтральная обычная форма) и 16 килограмм (разговорная счетная форма) .
Бит (англ. binary digit — двоичное число; также игра слов: англ. bit — кусочек, частица) — единица измерения количества информации, равная одному разряду в двоичной системе счисления. Обозначается по ГОСТ 8.417-2002. Для образования кратных единиц применяется с приставками СИ и с двоичными приставками.
Клод Шэннон в 1948 г предложил использовать слово bit для обозначения наименьшей единицы информации в статье A Mathematical Theory of Communication.
В зависимости от точек зрения, бит может определяться следующими способами:
Возможны две физические (в частности электронные) реализации бита (одного двоичного разряда):
В вычислительной технике и сетях передачи данных обычно значения 0 и 1 передаются различными уровнями напряжения либо тока. Например, в микросхемах на основе ТТЛ 0 представляется напряжением в диапазоне от +0 до +0,8 В, а 1 в диапазонеот +2,4 до +5,0 В.
В вычислительной технике, особенно в документации и стандартах, слово «бит» часто применяется в значении «двоичный разряд». Например: старший бит — старший двоичный разряд байта или слова, о котором идет речь.
Аналогом бита в квантовых компьютерах является кубит (q-бит).
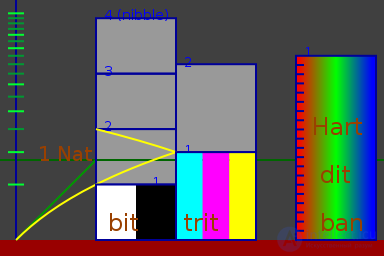
Бит (бело-черный) — одна из самых известных используемых единиц информации
Замена логарифма 2 на e, 3 или 10 приводит соответственно к редко употребляемым единицам нат,
трит и хартдит, равным соответственно 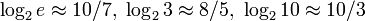 бита.
бита.
Трит — применяется в информатике, цифровой и вычислительной технике.
1 трит (трор) равен троичному логарифму 3-х возможных состояний (кодов) одного троичного разряда
1 трит (трор) = log3(3 [возможных состояний (кодов)])
1. Один трит, как один троичный разряд, может принимать три возможных значения (состояния, кода): 0, 1 и 2.
2. Один трит, как троичный логарифм 3-х возможных состояний (кодов) одного троичного разряда, может принимать только одно значение равное log33 = 1.
Способ устранения двойственности трита (трора)
Если за значением "1 троичный разряд" закрепить полные названия: троичный разряд и trinary digit, а за значениями "1 единица емкости ЗУ, 1 единица объема данных и 1 единица количества информации" закрепить сокращенные названия: трор и trit, то двойственность трита (трора) исчезнет.
Ёмкость одного троичного разряда и объем "0", "1" и "2"
Пустая ("0"), заполненная наполовину ("1") и заполненная полностью ("2") 1 тритная емкость.
"2" > "1" > "0", а один трит, как единица измерения емкости ЗУ, соответствует наибольшему возможному объему, т.е. значению троичного разряда - "2". Из этого следует, что значение троичного разряда равное "0" объема не занимает, а значение троичного разряда равное "1" занимает объем равный половине от наибольшего.
Очевидно, что модель на рисунке справа с наибольшим приближением описывается унарнокодированной троичной системой кодирования (UnaryCodedTernary, UCT), в которой: "0" - "", "1" - "1" и "2" - "11". В двоичных компьютерах унарнокодированной троичной системе кодирования соответствует двоичнокодированная унарнокодированная троичная система кодирования (BinaryCodedUnaryCodedTernary, BCUCT), в которой: "0" - "00", "1" - "01" и "2" - "11".
Единицы измерения информации бит, нат, трит и бан (децит)
При других основаниях логарифма, логарифмы 3-х возможных состояний (кодов) равны:
log2(3[возможных состояний]) = ln 3/ln 2 = 1,58... бита,
loge(3[возможных состояний]) = ln 3 = 1,09... ната
log3(3[возможных состояний]) = 1 триту
...
log10(3[возможных состояний]) = 0,477... бана (Хартли, дита, децита)
...
Трит — логарифмическая единица измерения в теории информации, минимальная целая единица измерения количества информации источников с тремя равновероятными сообщениями.Энтропию в 1 трит имеет источник информации с тремя равновероятными состояниями. Проще говоря, по аналогии с битом, который «уменьшает незнание» об исследуемом объекте в два раза, трит «уменьшает незнание» в три раза.
Применяется в теории информации.
По аналогии с понятием «байт» существует понятие « трайт ». Впервые термин использовался в ЭВМ троичной логики Сетунь-70, где он равнялся 6 тритам.
Аналогом трита в квантовых компьютерах является кутрит (q-трит).
Количество возможных состояний запоминающего устройства, состоящего из n элементарных ячеек, определяется в комбинаторике, при позиционном кодировании равно количеству размещений с повторениями и выражается показательной функцией:
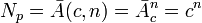 [возможных состояний], где
[возможных состояний], где
 — количество возможных состояний (кодов, значений) при позиционном кодировании,
— количество возможных состояний (кодов, значений) при позиционном кодировании,
 — количество размещений с повторениями,
— количество размещений с повторениями,
 — количество возможных состояний одного элемента запоминающего устройства, в SRAM - количество состояний триггера, в DRAM — количество распознаваемых уровней напряжения на конденсаторе, в устройствах с магнитной записью — количество распознаваемых уровней намагничивания на одном элементарном участке записи (один элементарный участок записи в устройствах записи на магнитную ленту, на магнитные барабаны, на магнитные диски — одна распознаваемая элементарная часть дорожки, в устройствах записи на ферритовые кольца — одно ферритовое кольцо),
— количество возможных состояний одного элемента запоминающего устройства, в SRAM - количество состояний триггера, в DRAM — количество распознаваемых уровней напряжения на конденсаторе, в устройствах с магнитной записью — количество распознаваемых уровней намагничивания на одном элементарном участке записи (один элементарный участок записи в устройствах записи на магнитную ленту, на магнитные барабаны, на магнитные диски — одна распознаваемая элементарная часть дорожки, в устройствах записи на ферритовые кольца — одно ферритовое кольцо),
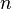 — количество троичных разрядов (троров, тритов) (элементов запоминающего устройства), в SRAM — количество триггеров, в DRAM — количество конденсаторов, в устройствах с магнитной записью — количество элементарных участков записи (в устройствах записи на магнитную ленту, на магнитные барабаны, на магнитные диски — количество распознаваемых элементарных участков дорожки, в устройствах записи на ферритовые кольца — количество ферритовых колец).
— количество троичных разрядов (троров, тритов) (элементов запоминающего устройства), в SRAM — количество триггеров, в DRAM — количество конденсаторов, в устройствах с магнитной записью — количество элементарных участков записи (в устройствах записи на магнитную ленту, на магнитные барабаны, на магнитные диски — количество распознаваемых элементарных участков дорожки, в устройствах записи на ферритовые кольца — количество ферритовых колец).
Так как прямая функция — зависимость количества состояний от количества разрядов — показательная, то обратная ей функция — зависимость количества разрядов от количества состояний — логарифмическая:
возьмем логарифм от обеих частей уравнения в предыдущем разделе, получим:
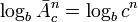 , где
, где
 — основание логарифма,
— основание логарифма,
выведем показатель степени за знак логарифма, получим:

поменяем местами обе части уравнения и перенесем сомножитель при 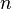 в правую часть в знаменатель дроби, получим:
в правую часть в знаменатель дроби, получим:
 , [троичных разрядов (троров, тритов)],
, [троичных разрядов (троров, тритов)],
при 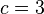 и применении троичного логарифма (
и применении троичного логарифма ( ) формула упрощается до:
) формула упрощается до:
 , [троичных разрядов (троров, тритов)].
, [троичных разрядов (троров, тритов)].
Цифровое запоминающее устройство представляет собой автомат с конечным числом состояний, причем возможен безусловный переход между любыми двумя произвольно выбранными состояниями.
|
Запоминающие устройства имеют одинаковую информационную емкость, если равны количества состояний, в которых они могут находиться. |
Если двоичное запоминающее устройство имеет 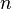 бит, то оно может принимать
бит, то оно может принимать
 возможных состояний.
возможных состояний.
Аналогично, если троичное устройство имеет  трит, то оно может принимать
трит, то оно может принимать
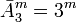 возможных состояний.
возможных состояний.
Частный случай 2.1
Приравнивая, получим, что емкость запоминающего устройства с  тритами равна
тритами равна 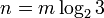 бит. Аналогично, емкость запоминающего устройства с
бит. Аналогично, емкость запоминающего устройства с 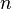 битами равна
битами равна  трит.
трит.
Таким образом:
6 тритов (длина машинного слова Сетуни) равны 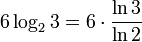 ≈ 9,51 бита. Следовательно, для кодирования машинного слова из 6 тритов требуется 10 битов.
≈ 9,51 бита. Следовательно, для кодирования машинного слова из 6 тритов требуется 10 битов.
1 байт равен  ≈ 5,047 трита. То есть, одного байта хватит для кодирования машинного слова длиной в 5 тритов.
≈ 5,047 трита. То есть, одного байта хватит для кодирования машинного слова длиной в 5 тритов.
1 килобайт равен 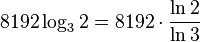 ≈ 5168,57 трита.
≈ 5168,57 трита.
Частный случай 2.2
1 трит равен 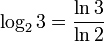 ≈ 1,585 бит.
≈ 1,585 бит.
Общий случай
В более общем случае отношение информационных емкостей двух запоминающих устройств с разными информационными емкостями элементов (разрядов) и с разным числом элементов (разрядов), выраженных в нелогарифмических единицах измерения емкости ЗУ и объема информации - в количествах возможных состояний, равно:
 где
где
 и
и  — количества возможных (вероятных) состояний элементарных ячеек сравниваемых запоминающих устройств,
— количества возможных (вероятных) состояний элементарных ячеек сравниваемых запоминающих устройств,
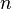 — количество элементарных устройств памяти запоминающего устойства в числителе,
— количество элементарных устройств памяти запоминающего устойства в числителе,
 — количество элементарных устройств памяти запоминающего устройства в знаменателе.
— количество элементарных устройств памяти запоминающего устройства в знаменателе.
Отношение является функцией от четырех аргументов, т.е. переменной.
Частный случай 1.1
Отношение информационных емкостей троичного (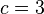 ) и двоичного (
) и двоичного ( ) запоминающих устройств с разными информационными емкостями (
) запоминающих устройств с разными информационными емкостями ( ), выраженными в нелогарифмических единицах измерения емкости ЗУ и объема информации - в количествах возможных состояний, равно:
), выраженными в нелогарифмических единицах измерения емкости ЗУ и объема информации - в количествах возможных состояний, равно:
 где
где
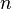 [битов] — количество элементарных двоичных устройств памяти (в двоичной SRAM - двоичных триггеров, в двоичной DRAM - конденсаторов с двумя распознаваемыми уровнями напряжений),
[битов] — количество элементарных двоичных устройств памяти (в двоичной SRAM - двоичных триггеров, в двоичной DRAM - конденсаторов с двумя распознаваемыми уровнями напряжений),
 [тритов] — количество элементарных троичных устройств памяти (в троичной SRAM - троичных триггеров, в троичной DRAM - конденсаторов с тремя распознаваемыми уровнями напряжений).
[тритов] — количество элементарных троичных устройств памяти (в троичной SRAM - троичных триггеров, в троичной DRAM - конденсаторов с тремя распознаваемыми уровнями напряжений).
Отношение является функцией от двух аргументов, т.е. переменной.
Частный случай 1.2
При сравнении информационных емкостей троичного запоминающего устройства и двоичного запоминающего устройства с одинаковым количеством элементов ( ), выраженных не в логарифмических единицах емкости носителя (объема информации) (бит, трит), а в нелогарифмических единицах количества информации - в количествах возможных состояний (значений, кодов):
), выраженных не в логарифмических единицах емкости носителя (объема информации) (бит, трит), а в нелогарифмических единицах количества информации - в количествах возможных состояний (значений, кодов):
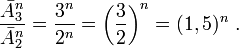
Отношение является функцией от одного аргумента, т.е. переменной, зависящей от числа разрядов - 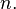
Частный случай 1.3
В еще более частном случае, при сравнении информационных емкостей одного элемента троичного запоминающего устройства и одного элемента двоичного запоминающего устройства ( ) выраженных в нелогарифмических единицах информации - в количествах возможных состояний:
) выраженных в нелогарифмических единицах информации - в количествах возможных состояний:

Отношение является константой (const), т.е. постоянной.
Следует отметить, что это не отношение логарифмических единиц измерения емкостей носителей и объемов информации - трита и бита, а отношение емкостей носителей и объемов информации, соответствующих триту и биту, выраженных в нелогарифмических единицах измерения емкостей носителей (ЗУ) и объемов информации - в количествах возможных состояний. Т.е. не отношение 1 трита к 1 биту, а отношение количеств возможных состояний устройств, соответствующих 1 триту и 1 биту.
Частный случай 2.1
При одинаковых информационных емкостях двоичного устройства памяти и троичного устройства памяти (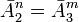 ), выраженных в нелогарифмических единицах измерения емкости ЗУ и объема информации - в количествах возможных состояний:
), выраженных в нелогарифмических единицах измерения емкости ЗУ и объема информации - в количествах возможных состояний:
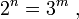
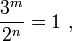
отношение является константой (const), т.е. постоянной, не зависящей от количества разрядов - 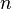 или
или  (при задании одного из двух количеств разрядов
(при задании одного из двух количеств разрядов 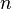 или
или  второе количество разрядов вычисляется).
второе количество разрядов вычисляется).
Возьмем натуральный логарифм от каждой из двух частей уравнения, при этом происходит переход от отношения количеств возможных состояний к натуральному логарифму отношения количеств возможных (вероятных) состояний:

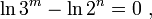
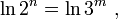

отметим, что произошел переход от отношения объемов (емкостей), выраженных в нелогарифмических единицах измерения емкости носителей и объемов информации - в количествах возможных состояний, к отношению логарифмов объемов (емкостей), т.е. к логарифмическим единицам измерения емкости носителей и объемов информации - битам и тритам,
выведем показатели степени за знак логарифма:
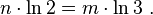
Из этого уравнения следуют две формулы:
1. для перевода логарифмической емкости троичного запоминающего устройства из тритов в биты:
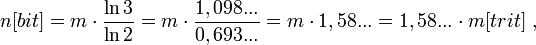
2. для перевода логарифмической емкости двоичного запоминающего устройства из битов в триты:

При емкости запоминающего устройства 6 тритов (длина машинного слова Сетуни)  и:
и:
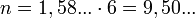 битов. Следовательно, для кодирования машинного слова из 6 тритов требуется 10 битов.
битов. Следовательно, для кодирования машинного слова из 6 тритов требуется 10 битов.
При емкости запоминающего устройства 9 тритов  и:
и:
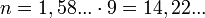 битов. Следовательно, для кодирования машинного слова из 9 тритов вполне достаточно 16 битов = 2 Байта.
битов. Следовательно, для кодирования машинного слова из 9 тритов вполне достаточно 16 битов = 2 Байта.
1байт = 28, т.е. n = 8 и:
 тритов. То есть, одного байта хватит для кодирования машинного слова длиной в 5 тритов.
тритов. То есть, одного байта хватит для кодирования машинного слова длиной в 5 тритов.
1 килобайт равен 213, т.е. n = 13 и:
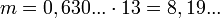 тритов.
тритов.
Частный случай 2.2
При сравнении информационных емкостей одного элемента троичного запоминающего устройства и одного элемента двоичного запоминающего устройства к условию 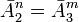 добавляется условие
добавляется условие  , при этом уравнение:
, при этом уравнение:
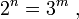 превращается в уравнение:
превращается в уравнение:
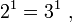 что не истинно, т.е. при наложенных условиях уравнение частного случая 2 решения не имеет, это означает, что для сравнения информационных емкостей одного элемента троичного запоминающего устройства и одного элемента двоичного запоминающего устройства уравнение частного случая 2 для этого частного случая не годится и в этом частном случае
что не истинно, т.е. при наложенных условиях уравнение частного случая 2 решения не имеет, это означает, что для сравнения информационных емкостей одного элемента троичного запоминающего устройства и одного элемента двоичного запоминающего устройства уравнение частного случая 2 для этого частного случая не годится и в этом частном случае
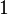 трит
трит  ≈ 1,585 бит.
≈ 1,585 бит.
Другими словами, так как уравнение в частном случае 2.1 было выведено при условии 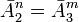 , а в данном частном случае
, а в данном частном случае  , то для данного случая оно не годится.
, то для данного случая оно не годится.
В этом частном случае нужно пользоваться уравнением из частного случая 1.3.
Таким образом, уравнение в частном случае 2.2 толкования 1 неправильное.
При бросании трехгранного (b = 3) «чижа», тринарная энтропия источника («чижа»)  с исходным алфавитом (цифры на гранях трехгранного «чижа»)
с исходным алфавитом (цифры на гранях трехгранного «чижа»)  (считывается цифра с грани лежащей на земле) и дискретным равномерным распределением вероятности (сечение «чижа» — равносторонний треугольник, плотность материала «чижа» однородна по всему объему «чижа»)
(считывается цифра с грани лежащей на земле) и дискретным равномерным распределением вероятности (сечение «чижа» — равносторонний треугольник, плотность материала «чижа» однородна по всему объему «чижа») 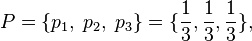 где
где  является вероятностью
является вероятностью 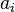 (
( ) равна:
) равна:
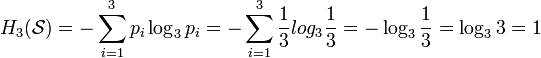 трит.
трит.
Трайт — минимальная непосредственно адресуемая единица главной памяти «Сетуни 70» Брусенцова.
Трайт равен 6 тритам (почти 9,51 бита). В «Сетуни 70» интерпретируется как знаковое целое число в диапазоне от -364 до 364.
Трайт достаточно велик, чтобы закодировать, например, алфавит, включающий русские и латинские заглавные и строчные буквы, цифры, математические и служебные знаки.
В трайте целое число как 9-ричных, так и 27-ричных цифр.
Куби́т (q-бит, кьюбит, кубит; от quantum bit) — квантовый разряд или наименьший элемент для хранения информации в квантовом компьютере.
Как и бит, кубит допускает два собственных состояния, обозначаемых 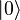 и
и  (обозначения Дирака), но при этом может находиться и в их суперпозиции, то есть в состоянии
(обозначения Дирака), но при этом может находиться и в их суперпозиции, то есть в состоянии 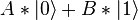 , где
, где  и
и 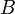 — комплексные числа, удовлетворяющие условию
— комплексные числа, удовлетворяющие условию 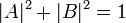 .
.
При любом измерении состояния кубита он случайно переходит в одно из своих собственных состояний. Вероятности перехода в эти состояния равны соответственно 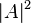 и
и 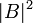 , то есть косвенно, по наблюдениям за множеством кубитов, мы все-таки можем судить об исходном состоянии.
, то есть косвенно, по наблюдениям за множеством кубитов, мы все-таки можем судить об исходном состоянии.
Кубиты могут быть связаны друг с другом, то есть на них может быть наложена ненаблюдаемая связь, выражающаяся в том, что при всяком изменении над одним из нескольких кубитов остальные меняются согласованно с ним. Иными словами, совокупность запутанных между собой кубитов может интерпретироваться как заполненный квантовый регистр. Как и отдельный кубит, квантовый регистр гораздо информативнее классического регистра битов. Он может не только находиться во всевозможных комбинациях составляющих его битов, но и реализовывать всевозможные тонкие зависимости между ними.
Несмотря на то, что мы сами не можем непосредственно наблюдать состояние кубитов и квантовых регистров во всей полноте, между собой они могут обмениваться своим состоянием и могут его преобразовывать. Тогда есть возможность создать компьютер, способный к параллельным вычислениям на уровне своего физического устройства, и проблемой остается лишь прочитать конечный результат вычислений.
Слово «qubit» ввел в употребление Бен Шумахер из Кеньон-колледжа (США) в 1995 г., а А. К. Звездин в своей статье предположил вариант перевода «q-бит» . Иногда также можно встретить название «квантбит».
Обобщением понятия кубит является кунит (Q-энк, куэнк; qudit), способный хранить в одном разряде более двух значений (например, кутрит англ. qutrit — 3, куквадрит — 4, …, куэнк — n) .
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про система кодирования информации Надеюсь, что теперь ты понял что такое система кодирования информации, бит, байт, трит, трайт, кубит и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Информатика
Комментарии
Оставить комментарий
Информатика
Термины: Информатика