Лекция
Сразу хочу сказать, что здесь никакой воды про табулирование функции, и только нужная информация. Для того чтобы лучше понимать что такое табулирование функции, табуляция функции , настоятельно рекомендую прочитать все из категории Информатика.
табулирование функции — это вычисление значений функции при изменении аргумента от некоторого начального значения до некоторого конечного значения с определенным шагом. Именно так составляются таблицы значений функций, отсюда и название — табулирование или табуляция. Необходимость в табулировании возникает при решении достаточно широкого круга задач. Например, при численном решении нелинейных уравнений f(x) = 0, путем табулирования можно отделить (локализовать)корни уравнения, то есть найти такие отрезки, на концах которых, функция имеет разные знаки. С помощью табулирования можно (хотя и очень грубо) найти минимумили максимум функции. Иногда случается так, что функция не имеет аналитического представления, а ее значения получаются в результате вычислений, что часто бывает при компьютерном моделировании различных процессов. Если такая функция будет использоваться в последующих расчетах (например, она должна бытьпроинтегрирована или продифференцирована и т. п.), то часто поступают следующим образом: вычисляют значения функции в нужном интервале изменения аргумента, то есть составляют таблицу (табулируют), а затем по этой таблице строят каким-либо образом другую функцию, заданную аналитическим выражением (формулой). Необходимость в табулировании возникает также при построении графиков функции на экране компьютера.
Табулирование функции – это вычисление значений функции для некоторого набора значений аргумента.
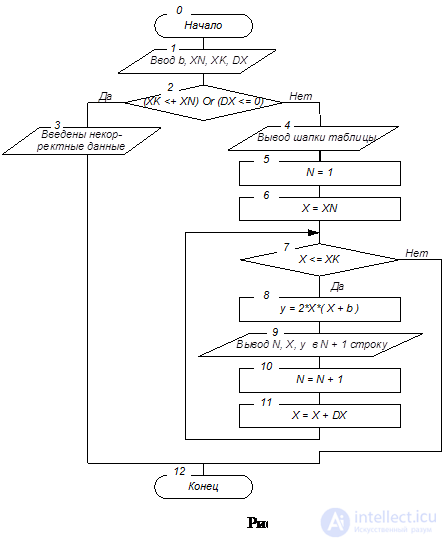
Пример 5.1. Выполнить табулирование функции y=2x(x+b) для переменной x, значение которой изменяется от начального до конечного значения с постоянным положительным шагом.
Результаты вычисления вывести на рабочий лист Excel.
Таблица соответствия переменных
| Обозначение в задании | Имя переменной | Тип переменной | Комментарий |
| y | y | вещественный | Результат. Значение функции |
| x | x | вещественный | Текущее значение аргумента функции |
| b | b | вещественный | Исходное данное. Числовая константа |
| Начальное значение x | XN | вещественный | Исходное данное |
| Конечное значение x | XK | вещественный | Исходное данное |
| Шаг изменения значения x | DX | вещественный | Исходное данное(>0) |
| N | целый | Номер итерации вычисления |
Анализ исходных данных:
| Имя переменной | Недопустимое значение | Ситуация |
| XN, XK | XN>XK | Ввод данных |
| DX | £0 | Ввод данных |
Вводимые значения переменных XN, XK и DX удобно проверять с помощью следующего логического выражения
(XK<=XN) Or (DX<=0)
Очевидно, что если это выражение истинно, то введенные данные некорректны.
Графическая схема алгоритма представлена на рис.5.2, результаты тестирования программы – на рис.5.3.
Sub Pr5_1()
Dim y As Single, x As Single, b As Single
Dim XN As Single, XK As Single, DX As Single
Dim N As Byte
'Ввод исходных данных
b = InputBox("Введи значение b")
XN = InputBox("Введи начальное значение х")
XK = InputBox("Введи конечное значение х")
DX = InputBox("Введи шаг изменения х")
'Проверка исходных данных
If (XK<=XN) Or (DX<=0) Then
Cells(1, 1) = "Введены некорректные данные:"
Cells(2, 1) = "XN=" & CStr(XN)
Cells(3, 1) = "XK=" & CStr(XK)
Cells(4, 1) = "DX=" & CStr(DX)
Else
'Выполнение расчетов и вывод результатов
Cells(1, 1) = "№"
Cells(1, 2) = "x"
Cells(1, 3) = "y"
N = 1
x = XN
While x <= XK
y = 2 * x * (x + b)
Cells(1 + N, 1) = N
Cells(1 + N, 2) = x
Cells(1 + N, 3) = y
 N = N + 1
N = N + 1
x = x + DX
Wend
Cells(1 + N + 1, 1) = "При b=" & CStr(b)
End If
End Sub
Пример 5.2. Выполнить табулирование функции
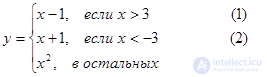
для переменной x, значение которой изменяется от начального до конечного значения с постоянным положительным шагом.
Результаты вычисления вывести в Excel. Об этом говорит сайт https://intellect.icu . Вывести номер формулы вычисления.
Таблица соответствия переменных
| Обозначение в задании | Имя переменной | Тип переменной | Комментарий |
| y | y | вещественный | Результат. Значение функции |
| x | x | вещественный | Текущее значение аргумента функции |
| Начальное значение x | XN | вещественный | Исходное данное |
| Конечное значение x | XK | вещественный | Исходное данное |
| Шаг изменения значения x | DX | вещественный | Исходное данное |
| N | целый | Номер итерации вычисления | |
| f | целый | Номер формулы вычисления |
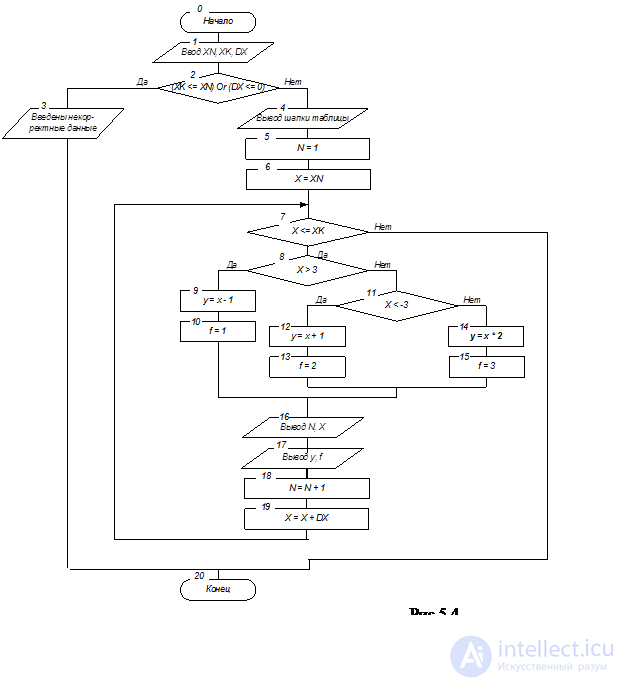
Анализ исходных данных: начальное, конечное значение переменной x и шаг ее модификации, - этого примера аналогичен анализу исходных данных примера 5.1. Однако требуется дополнительный анализ текущего значения аргумента функции, т.к. от его значения зависит выбор функциональной зависимости: по формуле 1, 2 или 3.

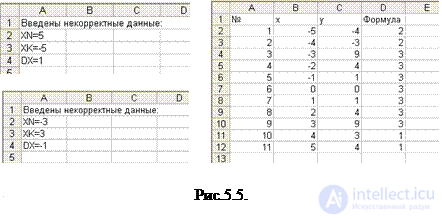
Графическая схема алгоритма представлена на рис.5.4, а результаты тестирования программы – на рис.5.5.
Sub Pr5_2()
Dim y As Single, x As Single
Dim XN As Single, XK As Single, DX As Single
Dim N As Byte, f As Byte
'Ввод и проверка исходных данных
XN = InputBox("Введи начальное значение х")
XK = InputBox("Введи конечное значение х")
DX = InputBox("Введи шаг изменения х")
If (XK<=XN) Or (DX<=0) Then
Cells(1, 1) = "Введены некорректные данные:"
Cells(2, 1) = "XN=" & XN: Cells(3, 1) = "XK=" & XK
Cells(4, 1) = "DX=" & DX
Else
'Выполнение расчетов и вывод результатов
Cells(1, 1) = "№": Cells(1, 2) = "x" ' Вывод шапки таблицы
Cells(1, 3) = "y": Cells(1, 4) = "Формула"
N = 1 ' Номер вычислений
For x = XN To XK Step DX ' Вычисления
If x >3 Then
y = x - 1: f = 1 ' По формуле 1
ElseIf x < -3 Then
y = x + 1: f = 2 ' По формуле 2
Else
y = x^2 : f = 3 ' По формуле 3
End If
Cells(1 + N, 1) = N: Cells(1 + N, 2) = x ' Номер вычислений и значение х
Cells(1 + N, 3) = y: Cells(1 + N, 4) = f ' Вывод y и номера формулы
N = N + 1 ' Модификация значения номера вычислений
Next
 End If
End If
End Sub
Для программирования циклических действий в приведенных выше примерах используются разные операторы цикла: в примере 5.1 – это оператор While … Wend, а в примере 5.2 – оператор For … Next.
Под табулированием функций в Mathcad понимается вычисление дискретных значений функции при изменении значения аргумента по закону арифметической прогрессии. При этом функция должна быть непрерывной на отрезке табулирования. Результаты табулирования в Mathcad принято представлять в виде таблиц. При табулировании необходимо определить значение дискретного аргумента, для чего задается идентификатор дискретного аргумента и определяется область его значений. Одним из способов задания значений дискретного аргумента, является задание счетчика значений дискретного аргумента или иначе – ранжированной переменной в Mathcad. Изменение аргумента задается в формате
x:=начальное значение[,начальное значение+шаг]..конечное значение
в скобках указан необязательный параметр, если его нет, шаг, по умолчанию, равен
1. Двоеточие ".." вводится символом точка с запятой ";" или кнопкой “m..n” панели инструментов “Матрицы”. В некоторых случаях в Mathcad возможно непосредственное задание значений дискретного аргумента, при этом нет необходимости задавать счетчик значений дискретного аргумента. Для каждого значения дискретного аргумента определяется значение функции. Пример табулирования функций представлен на листинге.
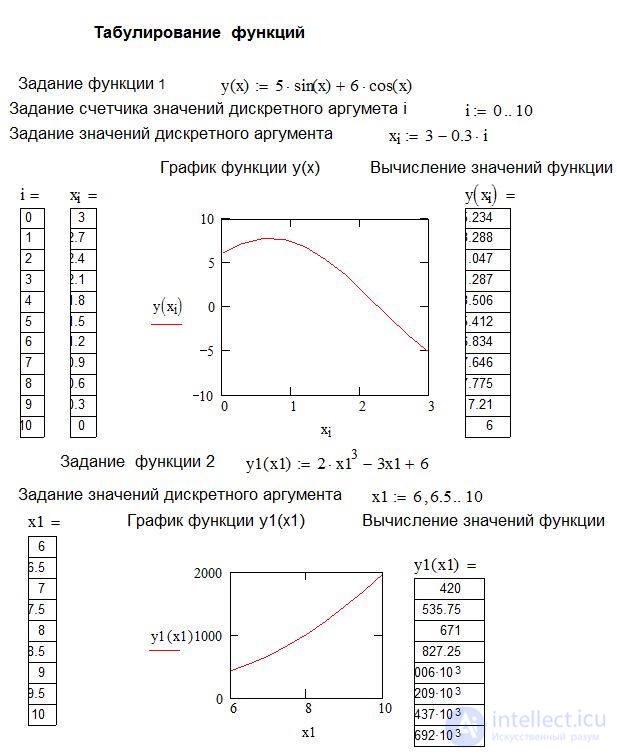
Рис пример табулирования в маткаде
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про табулирование функции Надеюсь, что теперь ты понял что такое табулирование функции, табуляция функции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Информатика
Из статьи мы узнали кратко, но содержательно про табулирование функции
Комментарии
Оставить комментарий
Информатика
Термины: Информатика