Лекция
Сразу хочу сказать, что здесь никакой воды про скорость, и только нужная информация. Для того чтобы лучше понимать что такое скорость, скорость материальной точки , настоятельно рекомендую прочитать все из категории Физические основы механики.
скорость (часто обозначается }, от англ. velocity или фр. vitesse, исходно от лат. vēlōcitās) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчета; по определению, равна производной радиус-вектора точки по времени . Этим же словом называют и скалярную величину — либо модуль вектора скорости, либо алгебраическую скорость точки, то есть проекцию этого вектора на касательную к траектории точки .

Термин «скорость» используют в науке и в широком смысле, понимая под ним быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят об угловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.
Расширениями понятия скорости являются четырехмерная скорость, или скорость в релятивистской механике, и обобщенная скорость, или скорость в обобщенных координатах.
Для характеристики движения материальной точки вводят векторную физическую величину - скорость, определяющую как быстроту движения, так и направление движения в данный момент времени.
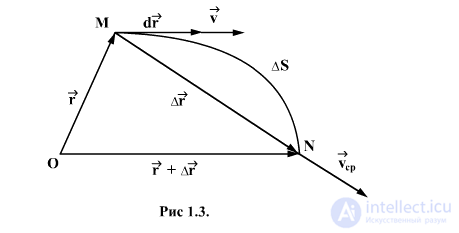
Пусть материальная точка движется по криволинейной траектории МN так, что в момент времени t она находится в т.М, а в момент времени 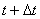 в т. N. Радиус-векторы точек М и N соответственно равны
в т. N. Радиус-векторы точек М и N соответственно равны  , а длина дуги МN равна
, а длина дуги МN равна 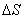 (рис. 1.3).
(рис. 1.3).
Вектором средней скорости 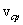 точки в интервале времени от t до t+Δt называют отношение приращения
точки в интервале времени от t до t+Δt называют отношение приращения 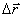 радиуса-вектора точки за этот промежуток времени к его величине
радиуса-вектора точки за этот промежуток времени к его величине 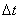 :
:
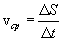 |
(1.5) |
Вектор средней скорости направлен также, как вектор перемещения 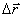 т.е. вдоль хорды МN.
т.е. вдоль хорды МN.
Мгновенная скорость или скорость в данный момент времени. Если в выражении (1.5) перейти к пределу, устремляя 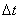 к нулю, то мы получим выражение для вектора скорости м.т. в момент времени t прохождения ее через т.М траектории.
к нулю, то мы получим выражение для вектора скорости м.т. в момент времени t прохождения ее через т.М траектории.
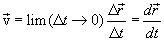 |
(1.6) |
В процессе уменьшения величины 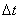 точка N приближается к т.М, и хорда МN, поворачиваясь вокруг т.М, в пределе совпадает по направлению с касательной к траектории в точке М. Поэтому вектор
точка N приближается к т.М, и хорда МN, поворачиваясь вокруг т.М, в пределе совпадает по направлению с касательной к траектории в точке М. Поэтому вектор 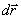 и скорость v движущейся точки направлены по касательной траектории в сторону движения. Вектор скорости v материальной точки можоразложить на три составляющие, направленные вдоль осей прямоугольной декартовой системы координат.
и скорость v движущейся точки направлены по касательной траектории в сторону движения. Вектор скорости v материальной точки можоразложить на три составляющие, направленные вдоль осей прямоугольной декартовой системы координат.
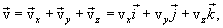 |
(1.7) |
где 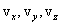 - проекции вектора скорости на оси координат х, у, z.
- проекции вектора скорости на оси координат х, у, z.
Подставляя в (1.6) значения для радиус-вектора материальной точки (1.1) и выполнив почленное дифференцирование, получим:
 |
(1.8) |
Из сопоставления выражений (1.7) и (1.8) следует, что проекции скорости материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих координат точки:
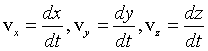 |
(1.9) |
Поэтому численное значение скорости:
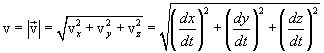 |
(1.10) |
Движение, при котором направление скорости материальной точки не изменяется, называется прямолинейным. Если численное значение мгновенной скорости точки остается во время движения неизменным, то такое движение называется равномерным.
Если же за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным.
В этом случае часто пользуются скалярной величиной 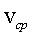 , называемой средней путевой скоростью неравномерного движения на данном участке
, называемой средней путевой скоростью неравномерного движения на данном участке 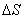 траектории. Она равна численному значению скорости такого равномерного движения, при котором на прохождение пути
траектории. Она равна численному значению скорости такого равномерного движения, при котором на прохождение пути 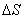 затрачивается то же время
затрачивается то же время 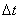 , что и при заданном неравномерном движении:
, что и при заданном неравномерном движении:
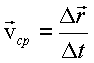 |
(1.11) |
Т.к. 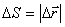 только в случае прямолинейного движения с неизменной по направлению скоростью, то в общем случае:
только в случае прямолинейного движения с неизменной по направлению скоростью, то в общем случае:
 .
.
Закон сложения скоростей. Если материальная точка одновременно участвует в нескольких движениях, то результирующее перемещения 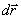 в соответствии с законом независимости движения, равно векторной (геометрической) сумме элементарных перемещений, обусловленных каждым из этих движений в отдельности:
в соответствии с законом независимости движения, равно векторной (геометрической) сумме элементарных перемещений, обусловленных каждым из этих движений в отдельности:
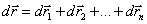
В соответствии с определением (1.6):
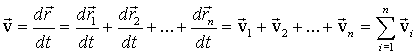 |
(1.12) |
Таким образом, скорость 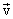 результирующего движения равна геометрической сумме скоростей
результирующего движения равна геометрической сумме скоростей 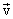 всех движений, в которых участвует материальная точка, (это положение носит название закона сложения скоростей).
всех движений, в которых участвует материальная точка, (это положение носит название закона сложения скоростей).
Небесная механика изучает поведение тел Солнечной системы и других небесных тел. Движение искусственных космических тел изучается в астродинамике. При этом рассматривается несколько вариантов движения тел, для каждого из которых необходимо придание определенной скорости. Для вывода спутника на круговую орбиту ему необходимо придать первую космическую скорость (например, искусственный спутник Земли); преодолеть гравитационное притяжение позволит вторая космическая скорость (например, объект запущенный с Земли, вышедший за ее орбиту, но находящийся в Солнечной системе); третья космическая скорость нужна чтобы покинуть звездную систему, преодолев притяжение звезды (например, объект запущенный с Земли, вышедший за ее орбиту и за пределы Солнечной системы); четвертая космическая скорость позволит покинуть галактику.
В небесной механике под орбитальной скоростью понимают скорость вращения тела вокруг барицентра системы.
Скорость звука — скорость распространения упругих волн в среде, определяется упругостью и плотностью среды. Скорость звука не является постоянной величиной и зависит от температуры (в газах), от направления распространения волны (в монокристаллах). При заданных внешних условиях обычно не зависит от частоты волны и ее амплитуды. В тех случаях, когда это не выполняется и скорость звука зависит от частоты, говорят о дисперсии звука. Впервые измерена Уильямом Дерхамом. Как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях скорость звука меньше, чем в твердых телах, поэтому при сжижении газа скорость звука возрастает.
Отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде называется числом Маха по имени австрийского ученого Эрнста Маха. Упрощенно, скорость, соответствующая 1 Маху при давлении в 1 атм (у земли на уровне моря), будет равна скорости звука в воздухе. Движение аппаратов со скоростью, сравнимой со скоростью звука, сопровождается рядом явлений, которые называются звуковой барьер. Скорости от 1,2 до 5 Махов называются сверхзвуковыми, скорости выше 5 Махов — гиперзвуковыми.
Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме. Традиционно обозначается латинской буквой «c» (произносится как [це]). Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчета (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.
Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году. Теперь ввиду современного определения метра скорость света считается равной точно 299792458 м/с[13].
Скорость гравитации — скорость распространения гравитационных воздействий, возмущений и волн. До сих пор остается не определенной экспериментально, но согласно общей теории относительности должна совпадать со скоростью света.
Линейная скорость:
Угловая скорость:
Автолик из Питаны в IV веке до н. э. определил равномерное движение так: «О точке говорится, что она равномерно перемещается, если в равные времена она проходит равные и одинаковые величины». Несмотря на то, что в определении участвовали путь и время, их отношение считалось бессмысленным[14], так как сравнивать можно было только однородные величины и скорость движения являлась чисто качественным, но не количественным понятием[15]. Живший в то же время Аристотель делил движение на «естественное», когда тело стремится занять свое естественное положение, и «насильственное», происходящее под действием силы. В случае «насильственного» движения произведение величины «двигателя» и времени движения равно произведению величины «движимого» и пройденного пути, что соответствует формуле , или
[14]. Этих же взглядов придерживался Авиценна в XI веке, хотя и предлагал другие причины движения[16], а также Герард Брюссельский в конце XII — начале XIII века. Герард написал трактат «О движении» — первый европейский трактат по кинематике — в котором сформулировал идею определения средней скорости движения тела (при вращении прямая, параллельная оси вращения, движется «одинаково с любой своей точкой», а радиус — «одинаково со своей серединой»)[17].
В 1328 году увидел свет «Трактат о пропорциях или о пропорциях скоростей при движении» Томаса Брадвардина, в котором он нашел несоответствие в физике Аристотеля и связи скорости с действующими силами. Брадвардин заметил, что по словесной формуле Аристотеля если движущая сила равна сопротивлению, то скорость равна 1, в то время как она должна быть равна 0. Он также представил свою формулу изменения скорости, которая хоть и была не обоснованна с физической точки зрения, но представляла собой первую функциональную зависимость скорости от причин движения. Брадвардин называл скорость «количеством движения»[18]. Уильям Хейтсбери, в трактате «О местном движении» ввел понятие мгновенной скорости. В 1330—1340 годах он и другие ученики Брадвардина доказали так называемое «мертонское правило», которое означает равенство пути при равноускоренном движении и равномерном движении со средней скоростью[19].
Всякая широта движения, униформно приобретаемая или теряемая, соответствует своему среднему градусу, так что столько же в точности будет пройдено благодаря этой приобретаемой широте, сколько и благодаря среднему градусу, если бы тело двигалось все время с этим средним градусом.
— «Мертонское правило» в формулировке Суайнсхеда
В XIV веке Жан Буридан ввел понятие импетуса[20], благодаря чему была определена величина изменения скорости — ускорение. Николай Орем, ученик Буридана, предложил считать, что благодаря импетусу ускорение остается постоянным (а не скорость, как полагал сам Буридан), предвосхитив, таким образом, второй закон Ньютона[21]. Орем также использовал графическое представление движения. В «Трактате о конфигурации качеств и движения» (1350) он предложил изображать отрезками перпендикулярных прямых количество и качество движения (время и скорость), иными словами, он нарисовал график изменения скорости в зависимости от времени[22].
По мнению Тартальи, только вертикальное падение тела является «естественным» движением, а все остальные — «насильственные», при этом у первого типа скорость постоянно возрастает, а у второго — убывает. Два этих типа движения не могут проистекать одновременно. Тарталья считал, что «насильственные» движения вызваны ударом, результатом которого является «эффект», определяемый скоростью[23]. С критикой работ Аристотеля и Тартальи выступал Бенедетти, который вслед за Оремом пользовался понятиями импетуса и ускорения[24].
В 1609 году в работе «Новая астрономия» Кеплер сформулировал закон площадей, согласно которому секторная скорость планеты (площадь, описываемая отрезком планета — Солнце, за единицу времени) постоянна[25]. В «Началах философии» Декарт сформулировал закон сохранения количества движения, которое в его понимании есть произведение количества материи на скорость[26], при этом Декарт не принимал во внимание тот факт, что количество движения имеет не только величину, но и направление[27]. В дальнейшем понятие «количество движения» развивал Гук, который понимал его как «степень скорости, присущей в определенном количестве вещества»[28]. Гюйгенс, Валлис и Рен добавили к этому определению направление. В таком виде во второй половине XVII века количество движения стало важным понятием в динамике, в частности в работах Ньютона и Лейбница[29]. При этом Ньютон не определял в своих работах понятие скорости[30]. По-видимому, первая попытка явного определения скорости была сделана Валлисом в его трактате «Механика или геометрический трактат о движении» (1669—1671): «Скорость есть свойство движения, отражающееся в сравнении длины и времени; а именно, она определяет, какая длина в какое время проходится»[31].
В XVII веке были заложены основы математического анализа, а именно интегрального и дифференциального исчисления. В отличие от геометрических построений Лейбница, теория «флюксий» Ньютона строится на потребностях механики и имеет в своем основании понятие скорости. В своей теории Ньютон рассматривает переменную величину «флюенту» и ее скорость изменения — «флюксию»[32].
| Метры в секунду | |
|---|---|
| Скорость света | 299 792 458 |
| Скорость движения самых далеких галактик | |
| Скорость электронов в кинескопе телевизора | |
| Скорость движения Солнца по орбите вокруг центра Галактики | |
| Скорость движения Земли по орбите вокруг Солнца | |
| Скорость искусственного спутника Земли | |
| Скорость движения Луны по орбите вокруг Земли | |
| Максимальная скорость пассажирского реактивного самолета | |
| Средняя скорость молекулы азота при температуре 0 град С | |
| Максимальная скорость автомобиля | |
| Максимальная скорость локомотива на железной дороге | |
| Максимальная скорость полета сокола | |
| Скорость гепарда | |
| Рекорд скорости человека в беге на дистанции 100 м | |
| Рекорд скорости человека в ходьбе на 50 км | |
| Скорость черепахи | |
| Скорость улитки |
Статью про скорость я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое скорость, скорость материальной точки и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики