3.8. Центр инерции системы

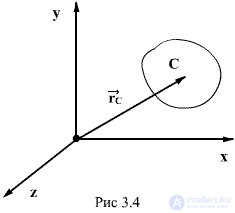
В рассматриваемом выше уравнении Ньютона предполагалось, что тело имеет настолько малые размеры, что его можно считать материальной точкой. Движение любого недеформируемого тела конечных размеров может быть описано уравнениями, аналогичными (3.6), если ввести понятие «центра масс» («центра инерции») тела. Если тело состоит из n материальных точек с массами 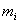 и радиус-векторами 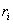, то центром масс системы материальных точек называют такую т.С, радиус-вектор которой определяется следующим образом:

(3.7)

где 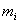 и 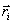 - масса и радиус-вектор i-ой точки системы, m - общая массавсей системы.

Соответственно соотношения между декартовыми координатами центра инерции и всех точек системы имеют вид:

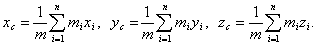
Скорость центра инерции:

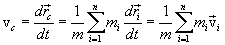(3.8)

Импульс системы. Геометрическую сумму импульсов всех материальных точек системы называют импульсом системы и обозначают буквой :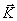

,

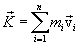тогда скорость центра масс

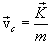(3.9)

Таким образом, из (3.9) следует, что импульс системы равен произведению массы всей системы на скорость ее центра инерции:

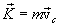(3.10)