4. Закон сохранения энергии и момента импульса,работа,Потенциальная и кинетическая энергия, Закон сохранения энергии

Привет, Вы узнаете о том , что такое закон сохранения энергии, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое закон сохранения энергии, закон сохранения момента импульса, работа силы, равновесие механической системы, применение законов сохранения , настоятельно рекомендую прочитать все из категории Физические основы механики.

Если тело движется под действием силы, то говорят, что сила совершает работу. В механике с работой тесно связано понятие энергии.

Наверно, энергия — самое известное понятие физики, о котором так или иначе наслышаны многие люди. История развития представлений об энергии была достаточно драматичной. На протяжении сорока лет велись споры между сторонниками Декарта и Лейбница. Первые утверждали, что при соударениях тел остается неизменной произведение массы на значение скорости (Декарт понимал импульс в алгебраическом смысле, а не в векторном), вторые отстаивали сохранение произведения массы на квадрат скорости, называвшееся тогда живой силой. Как часто случается, правы оказались обе стороны: при упругих соударениях сохраняется как вектор количества движения, так и живая сила, которую теперь называют кинетической энергией.

Впоследствии выяснился глубокий физический смысл закона сохранения энергии, который оказался связан с фундаментальной симметрией нашего мира — однородностью времени. Ученые обнаружили новые формы энергии, а закон сохранения полной энергии стал непременным атрибутом всех физических теорий. В этом разделе мы начинаем знакомство с простейшими формами энергии — потенциальной энергией тела в силовом поле и кинетической энергией движущегося тела.

4.1. работа силы

Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы, сделанных из пластилина. Если эти шары летят друг на друга с одной и той же скоростью, то при соударении они прилипнут друг к другу и остановятся. В этом случае суммарный импульс обоих шаров остался равным нулю, хотя состояние системы изменилось. Шары при этом нагрелись. Этот пример показывает, что импульс не всегда может служить мерой движения. Такой мерой является энергия. В данном случае механическая энергия при ударе перешла в другой вид энергии (тепловую).

Сначала рассмотрим важную характеристику — работу. Пусть материальная точка движется по траектории AB (рис. 1). На точку во время движения действует в общем случае переменная сила F. На участке ds (настолько малом, что модуль перемещения равен пройденному пути) силу F можно считать постоянной.

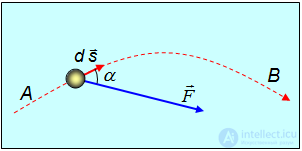
Рис 4.1. Элементарная работа

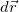
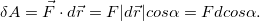
Работа — скалярная величина, ее знак зависит от знака . Положительная работа совершается силой, если ее направление составляет острый угол с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол с направлением движения, при этом сила тормозит это движение. Величина

— это проекция силы F на направление перемещения. Следовательно,

Полная работа силы находится как сумма (интеграл) элементарных работ по всей траектории L точки:

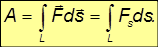
При перемещении вдоль оси x работу графически можно представить как площадь под кривой F_x(x) (рис. 4.2), причем площади под осью абсцисс следует приписывать отрицательное значение.

Рис. 2. Графическая интерпретация работы силы. Здесь для краткости положено F = F_x(x)

Если перемещение ортогонально силе, то = 0 и работа равна нулю:

Последнее показывает, что понятие работы в механике отлично от обыденного представления о работе. Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и 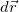= 0. Здесь и ниже 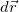и 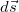означают одно и то же — бесконечно малое перемещение, а |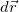|=||=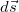 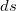— соответствующий бесконечно малый путь.

Если на тело действует несколько сил, то

то есть работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности.

Рассмотрим для примера работу, совершаемую внешней силой по сжатию и растяжению пружины с жесткостью 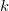. Направим ось 0x вдоль пружины, причем за начало координат 0 выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины. Тогда согласно закону Гука

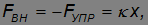
где x — удлинение пружины. При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).

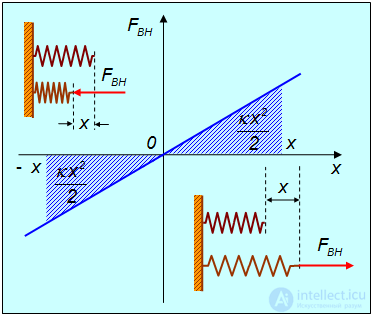
Рис. 4.3. Работа, совершаемая при сжатии/растяжении пружины

Скалярное произведение для элементарной работы внешней силы имеет в этом случае вид

так что для полной работы упругой деформации пружины получаем

Заметим, что A не зависит от знака x: и при растяжении, и при сжатии пружины внешняя сила совершает одну и ту же положительную работу.

4.2. Кинетическая энергия

Запишем уравнение движения материальной точки:

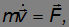
где F — результирующая сила. Умножим уравнение движения скалярно на ds = vdt:

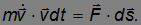
В правой части уравнения мы получили элементарную работу 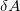, в левой — выражение, которое можно преобразовать к виду полного дифференциала:

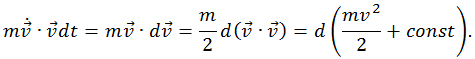
В результате имеем

то есть элементарная работа, совершенная силой F при перемещении ds материальной точки массой m равна приращению величины mv₂/2 + const. По размерности это энергия (энергия имеет ту же размерность, что и работа). Получается, что сила совершает некоторую работу, и на такое же количество возрастает указанная величина с размерностью энергии, причем энергии, обусловленной самим фактом движения со скоростью v. Поэтому в нерелятивистской (ньютоновской) механике произвольную константу полагают равной нулю, а то, что осталось, называют кинетической энергией частицы массы m, движущейся со скоростью v. Будем обозначать кинетическую энергию буквой K, другое общепринятое обозначение: буква T. Таким образом, по определению:

Кинетическую энергию материальной точки можно также выразить через ее импульс :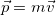

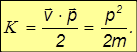
Если F = 0 (система замкнута), то работа сил равна нулю, следовательно, равно нулю приращение кинетической энергии. Иными словами, кинетическая энергия в этом случае сохраняется: К = const. На этом уровне нашего знакомства с законами природы трудно обнаружить особый смысл в введении нового понятия — кинетической энергии, поскольку она полностью определяется импульсом частицы. Но не будем торопиться с выводами. Вся глубина понятия энергии будет выявлена в дальнейшем, когда выяснится, что кинетическая энергия — лишь одна из многочисленных форм энергии.

Выражение для кинетической энергии устанавливает единицу измерения энергии.

Пример. Найти кинетическую энергию Земли в ее годичном движении вокруг Солнца. Расстояние до Солнца R = 150 млн. км, масса Земли равна M_З = 6 • 1024 кг.

Мы знаем, что расстояние

Земля преодолевает за время

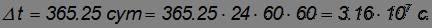
Отсюда скорость орбитального движения Земли равна

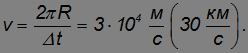
Кинетическая энергия Земли будет равна

На рис. 4.4 показаны характерные значения энергий некоторых физических процессов.

Рис. 4.4. Энергия некоторых физических процессов

4.3. Мощность

Представим снова элементарную работу в виде

Другими словами, мощность, развиваемая некоторой силой, равна скорости, с которой эта сила производит работу. Можно сказать и так: средняя за единицу времени мощность численно равна работе совершенной за единицу времени. Если мощность за выбранную единицу времени практически не меняется, то слово «средняя» можно опустить: мощность численно равна работе за единицу времени.

Как видно из определения, мощность равна скалярному произведению силы на скорость перемещения ее точки приложения, поэтому работа силы за время от t₁ до t₂ может быть вычислена следующим образом:

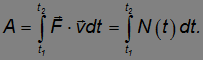
Средняя мощность за этот же промежуток времени равна

За единицу мощности принимается такая мощность, при которой в единицу времени совершается единица работы.

Внесистемная единица мощности — лошадиная сила (л.с.) — равна 736 Вт. В быту часто используют единицу энергии — 1 кВт•ч = 103 Вт•3600 с=3.6 МДж.

Пример. Вертолет массой m = 3 m висит в воздухе. Определить мощность, развиваемую мотором вертолета, если диаметр ротора равен d = 8 м. При расчете принять, что ротор отбрасывает вниз цилиндрическую струю воздуха диаметром, равным диаметру ротора. Плотность воздуха 1.29 кг/м3.

При решении этой задачи надо применить все известные нам законы динамики. Поскольку это — не одно- и не двухходовая задача, попробуем сначала найти вид окончательного выражения, пользуясь анализом размерности (см. тему 1.3). Искомая мощность зависит от: 1) веса вертолета mg; 2) диаметра винта d, 3) плотности воздуха 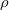, то есть искомая формула должна иметь вид

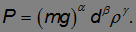
Размерность мощности будет [N] = [ML2T–3]. Составляем равенство размерностей в обеих частях искомой формулы:

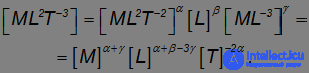
Решая систему уравнений

находим

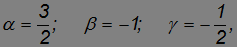
то есть искомая мощность двигателя вертолета будет

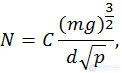
где C — некий числовой коэффициент.

Решим теперь эту же задачу точно. Пусть — скорость струи воздуха, отбрасываемой винтом. За время частицы воздуха проходят расстояние 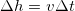. Иными словами, за время винт вертолета придает скорость всем частицам воздуха, находящимся в цилиндре с площадью основания 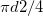и высотой 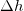. Масса воздуха 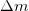в этом объеме равна

а его кинетическая энергия 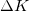дается выражением

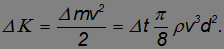
Поскольку мотор передает воздуху кинетическую энергию 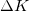, то такова и совершаемая им работа. Поэтому развиваемая мотором мощность (без учета потерь мощности во всех трансмиссиях на пути от двигателя до винта) равна

В этом выражении нам надо еще найти скорость струи воздуха, отбрасываемой винтом. Импульс , передаваемый частицам воздуха за время , равен

Из второго закона Ньютона следует, что средняя сила, действующая на отбрасываемый вниз воздух равна 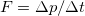. По третьему закону Ньютона такая же сила действует на вертолет со стороны воздуха. Эта сила компенсирует вес вертолета:

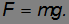
Отсюда получаем уравнение

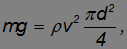
позволяющее найти скорость струи воздуха:

Подставляя найденную скорость в выражение для мощности двигателя вертолета, получаем окончательный результат:

Мы видим, что выражение для мощности действительно оказалось таким, каким ожидалось на основе анализа размерностей. Подставляя числовые данные, находим

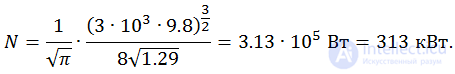
Рис.4.5. Мощность в природе и технике

4.4. Потенциальная энергия

Выше мы уже получили выражение для работы, совершаемой при растяжении пружины. Рассмотрим следующую систему. Нерастянутая пружина лежит на гладкой горизонтальной плоскости, один ее конец закреплен, а ко второму прикреплен грузик массой m. Начало координатной оси поместим в точку, где находится свободный конец пружины. Мы оттягиваем пружину на расстояние х_max и отпускаем грузик без начальной скорости. Каково движение грузика?

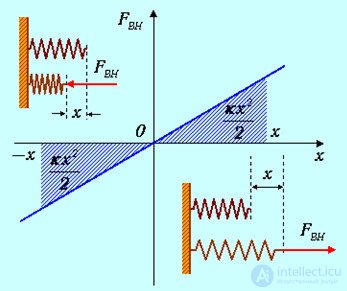
Рис 4.6. Работа при изменении длины пружинки.

В горизонтальной плоскости на грузик действует только упругая сила деформированной пружины, стремящаяся вернуть его к началу координат (положению равновесия). Под действием этой силы грузик приходит в движение. Если его координата в какой-то момент времени равна x, то в этот момент на грузик действует со стороны пружины упругая сила . Поэтому уравнение движения грузика имеет вид

Умножим обе части равенства на скорость грузика

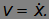
Произведение в левой части можно представить в виде производной

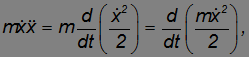
а произведение в правой части — в виде производной

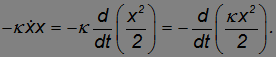
Поэтому уравнение движения грузика можно записать теперь в виде

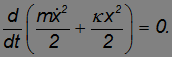
Раз производная выражения в скобках равна нулю, само это выражение не зависит от времени, оно постоянно (сохраняет свое начальное значение):

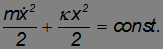
Как бы ни двигался грузик на пружинке, выписанная сумма двух слагаемых не меняется. В первом слагаемом мы узнаем кинетическую энергию грузика, а во втором — работу по растяжению (сжатию) пружины на расстояние х. Совершив эту работу, мы запасаем энергию упругой деформации пружины (ее называют потенциальной энергией). В любой момент времени грузик обладает какой-то кинетической энергией, а пружина — потенциальной.

Значение постоянной интегрирования в выражении для полной механической энергии системы «грузик — пружинка» находим, вспоминая начальные условия: при t = 0 мы отпустили грузик без начальной скорости v(0) = 0 на расстоянии x(0) = х_max от начала координат. Отсюда полная механическая энергия системы будет равна

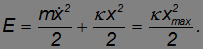
В начальный момент времени кинетическая энергия грузика равна нулю, и полная энергия системы равна той работе, которую мы сначала совершили, растянув пружину на расстояние х_max. Затем груз двигается к началу координат с возрастающей скоростью. В момент прохождения положения равновесия (х = 0) потенциальная энергия пружины равна нулю, следовательно, кинетическая достигает максимума. Грузик проходит положение равновесия, сила упругости меняет знак и начинает его тормозить. Скорость груза обращается в нуль при х = –х_max , когда полная энергия системы снова состоит лишь из потенциальной энергии (на этот раз сжатой) пружины. Далее процесс "перекачки" потенциальной энергии в кинетическую и обратно повторяется.

На этом частном примере мы заметили, что

• сохраняется полная энергия Е системы «грузик-пружинка», равная сумме кинетической энергии К = mv²/2 грузика и потенциальной энергии П = kх²/2 пружинки;
• потенциальная энергия пружины связана с работой по ее растяжению (сжатию): П = А_внеш ;
• силу упругости F = –kх = –F_внеш со стороны деформированной пружины можно получить дифференцированием потенциальной энергии по координате:

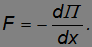
Потенциальное поле сил. Обобщим теперь наш частный случай. Пусть на частицу в каждой точке пространства действует определенная сила F (r,t), зависящая только от положения частицы и, быть может, от времени. Поскольку действующая сила не зависит от движения частицы, мы можем считать ее атрибутом пространства. В этом случае говорят, что в пространстве задано силовое поле. Например, поле тяжести Земли мы можем рассматривать как внешнее силовое поле по отношению к таким телам, движущимся в этом поле, как люди, автомобили, поезда, самолеты, спутники, вода в реках, облака в небе и так далее, по той простой причине, что их движение никак не влияет на характеристики этого поля. Совершенно очевидно, что это обусловлено размерами Земли.

Видео 4.1. Баллистический маятник — двухстадийный процесс демонстрация сохранения импульса на первом этапе и сохранения полной механической энергии на втором этапе.

Среди силовых полей мы выделим потенциальные поля, которые можно описать некоторой скалярной функцией

такой, что

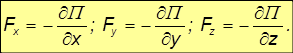
Здесь F_x, F_{y, Fz} проекции силы на направления осей некоторой декартовой системы координат, ее разложение по базису имеет вид

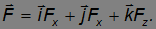
Как будет видно из дальнейшего, связь потенциальной энергии и силы оказывается действительно полезной, когда функция П не зависит от времени. Только этот случай и будет рассматриваться на протяжении всего курса.

Выражение для вектора силы можно записать более компактно. Для этого вводят операцию градиент — своего рода «векторное» дифференцирование функции (не путать с просто дифференцированием вектора, например, по времени):

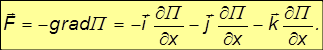
Знак минус, поставленный впереди, к операции «градиент» отношения не имеет и присутствует в выражении для вектора силы ради удобства (см. пример с пружиной выше и текст ниже) Применение операции «градиент» (grad) к скалярному полю (скалярной функции координат) порождает векторное поле. Ясно, что расчеты движения в потенциальных полях должны быть проще хотя бы потому, что вместо трех функций (проекций силы) мы будем иметь дело лишь с одной функцией П(x,y,z)..

Рассмотрим стационарное потенциальное силовое поле (то есть потенциальное поле П(x,y,z), не зависящее явно от времени). Найдем элементарную работу сил поля при перемещении ds:

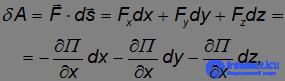
то есть элементарная работа

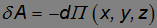
представляется как взятый с обратным знаком полный дифференциал функции П. С другой стороны, поскольку работа равна приращению кинетической энергии тела

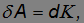
получаем отсюда

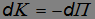
или

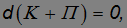
то есть сохраняется сумма

Таким образом, для стационарных потенциальных полей справедливы все выводы, сделанные нами при рассмотрении частного случая грузика на пружинке. Стало быть, скалярная функция П (r), описывающая такое поле, есть не что иное как потенциальная энергия частицы в этом силовом поле.

Консервативные силы. Проинтегрируем полученное соотношение

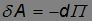
вдоль траектории тела и получим важное свойство стационарных потенциальных полей:

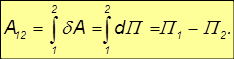
Здесь П₁ = П(r₁) и П₂ = П(r₂) — значения потенциальной энергии в начальной r₁ и конечной r₂ точках перемещения. Соотношение, связывающее работу силы и изменение потенциальной энергии тела, означает, что

Если работа сил поля положительна (частица перемещается под действием сил поля), то ее потенциальная энергия уменьшается: П₂ < П₁. Если же работа сил поля отрицательна (например, внешняя сила вынуждает частицу двигаться против сил поля), то потенциальная энергия частицы увеличивается. Растягивая пружину в нашем примере, мы совершали работу против сил упругости и увеличивали потенциальную энергию системы.

Действительно, в этом случае начальная и конечная точки совпадают, П₂ = П₁ и A₁₂ = 0. Покажем это более детально. Рассмотрим две произвольные точки 1 и 2 и два произвольных пути I и II, их соединяющих (рис. 4.7).

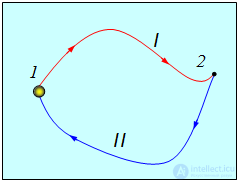
Рис 4.7. Работа при перемещении тела по замкнутому контуру

Пусть поле сил консервативно, то есть работы на этих путях совпадают:

Переместим теперь тело из точки 1 в точку 2 по пути I, а затем — из точки 2 в точку 1 по пути II. Об этом говорит сайт https://intellect.icu . Полная совершенная работа по замкнутому контуру равна сумме

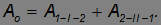
Сравним работы на пути II, проходимом в прямом и обратном направлениях. В каждой точке пути действуют те же силы, но изменение направления движения на обратное приводит к замене ds нa –ds. Таким образом, искомая работа равна

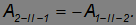
Учитывая полученные соотношения, переписываем выражение для работы по замкнутому контуру в виде

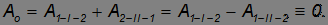
Мы доказали эквивалентность утверждений, что 1) работа консервативных сил не зависит от формы траектории и 2) работа таких сил при обходе замкнутого контура равна нулю.

Итак, стационарное потенциальное поле консервативно. Но верно и обратное: консервативное поле потенциально. Покажем это. Берем произвольную точку r₀ и задаем в этой точке произвольное значение потенциальной энергии П(r₀). При переходе из точки r₀ в любую другую точку r совершается работа A₀₁, не зависящая от пути перехода. Поэтому можно определить функцию П для каждой точки равенством

Подчеркнем еще раз: задать функцию П в каждой точке пространства можно лишь вследствие независимости работы от пути. Иначе, проходя из точки r0 в точку r, мы получали бы разные результаты, и функция П была бы неоднозначной (точнее непрерывно бесконечнозначной).

Применим полученное выражение для соседней точки r+dr:

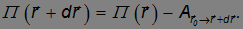
Работу по перемещению из точки r0 в точку r+dr представим как сумму работ по перемещению из r0 в r и из r в r+dr:

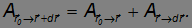
(снова пользуясь независимостью работы от пути). Проведя преобразования, получим

Слева стоит приращение –dП, а справа — элементарная работа 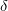A. Полученное соотношение

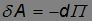
влечет за собой, как мы видели, сохранение величины К+П, то есть введенная нами функция П действительно является потенциальной энергией системы. Таким образом, поле консервативных сил потенциально.

Не следует думать, что все поля в природе потенциальны, а силы — консервативны. Например, силы трения или сопротивления среды всегда направлены против перемещения и, следовательно, имеют одинаковый знак на всей траектории тела. При суммировании элементарных работ по замкнутому пути мы не получим нуля: работа будет зависеть от длины пройденного пути. Значит, эти силы не консервативны.

Произвольная постоянная П(r₀), фигурирующая в формуле для изменения потенциальной энергии, не играет роли, так как физически наблюдаемым является изменение потенциальной энергии, а не ее абсолютное значение. Часто, когда это возможно, в качестве r₀ выбирают бесконечно удаленную точку, и полагают значение потенциальной энергии в ней равной нулю. Но этот выбор не всегда возможен, как демонстрируется в следующем разделе.

Постоянное однородное поле сил тяжести. Вблизи поверхности Земли все тела падают с постоянным ускорением g, направленным к центру планеты. Если мы рассматриваем движение в области, линейные размеры которой много меньше радиуса Земли, земную поверхность можно считать плоской. В этом приближении поле тяжести однородно: силы, действующие на тело, в любой точке имеют одинаковое направление и величину F = mg. Покажем потенциальность поля силы тяжести у поверхности Земли (рис. 4.8).

Рис. 4.8. Нахождение потенциальной энергии поля сил тяжести

Элементарная работа при перемещении ds равна

где –dh — проекция перемещения на направление действия силы, то есть dh — изменение высоты тела. Полная работа при перемещении тела из точки 1 в точку 2 равна

Таким образом, в поле сил тяжести работа не зависит от пути, по которому движется частица, а определяется только начальным и конечным положениями частицы в пространстве. Соответственно, потенциальная энергия в поле сил тяжести находится в соответствии с общим рецептом как

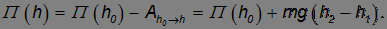
Если отсчитывать высоту от поверхности Земли, приписав при этом точке на поверхности нулевую потенциальную энергию П(h₀ = 0) = 0, для произвольной высоты h получим хорошо знакомую формулу

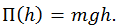
Или в векторном виде

(4.4.1)

В последней формуле радиус вектор 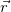начинается в любой точке лежащей на поверхности Земли, потенциальная энергия на поверхности Земли, как и ранее, принята равной нулю.

Пример. Исходя из уравнений движения, показать сохранение полной энергии тела, движущегося в однородном поле силы тяжести.

Решение. Учитывая (4.4.1), запишем полную механическую энергию тела в виде

(4.4.2)

Сохранение во времени некоторой величины означает, что полная производная по времени от этой величины в любой момент времени равна нулю. И обратно, если полная производная по времени от некоторой величины равна нулю тождественно (в любой момент времени), то эта величина сохраняется. Вычислим полную производную по времени механической энергии из (4.4.2):

(4.4.3)

При получении (4.4.3) было учтено, что 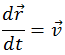и, согласно уравнению движения, ускорение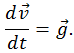

Видео 4.2. Маятник Галилея — демонстрация сохранения полной механической энергии при движении в однородном поле тяжести.

Поле центральных сил

Другой пример. Вычислим работу произвольной центральной стационарной силы при перемещении ее точки приложения из некоторой произвольной точки пространства 1, находящейся на расстоянии r₁ до центра поля, в некоторую произвольную точку 2, находящуюся на расстоянии r₂ от центра поля. Воспроизведенные ниже выкладки показывают, что траектория перемещения точки приложения силы может быть любой — результат не зависит от ее формы.

Общий вид центральной силы следующий

(4.4.4)

Здесь радиус-вектор 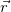начинается в центре поля. Примерами могут служить поле точечного электрического заряда, находящегося в начале координат, или гравитационное поле сферически симметричного объекта с центром в начале координат. Подставив (4.4.4) в общее определение работы, получаем:

(4.4.5)

Криволинейный интеграл вида (4.4.5) легко превращается в обычный интеграл с помощью весьма полезного тождества (4.4.6) ниже. Дифференцируя определение квадрата модуля вектора

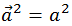
и сокращая на двойку имеем для любого вектора:(4.4.6)

(4.4.6)

То есть, скалярное произведение вектора на его приращение равно произведению модуля этого вектора на приращение его модуля. Заменяя в (4.4.5) скалярное произведение на обычное произведение rdr и сокращая на r, получаем

(4.4.7)

Если функция φ(r) есть первообразная для f(r), то окончательно имеем:

(4.4.8)

Из формулы (4.4.8) видно, что величина работы определяется только положением начальной и конечной точек и действительно не зависит от формы траектории перемещения точки приложения силы. Часто говорят короче: работа не зависит от пути. Работа получилась равной приращению первообразной φ(r), поэтому отождествлять ее с потенциальной энергией неудобно: получится, что при совершении положительной работы растет и функция f(r). Потенциальная энергия вводится как П = –φ(r), тогда, при совершении положительной работы, потенциальная энергия убывает и можно говорить и так: работа совершается за счет убыли потенциальной энергии тела в силовом поле. Тогда

(4.4.9)

Вычисление интеграла с помощью тождества (4.4.6) иллюстрирует следующий рисунок

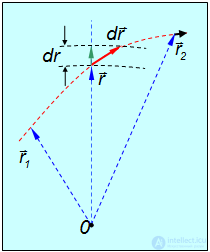
Рис. 4.8. Работа центральной силы

Положив потенциальную энергию в точке с радиус-вектором равной 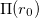, для ее значения в произвольной точке с радиус-вектором 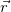, получим

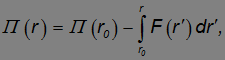
Покажем, что операция «градиент», примененная к потенциальной энергии П(r), действительно дает нам поле центральных сил, направленных по радиус-вектору 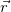и с модулем F(r). Берем производную от П(r) по координате x как производную сложной функции:

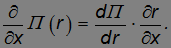
Производная по r вычисляется без труда из формулы для потенциальной энергии:

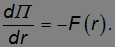
Производная r по x равна

Таким образом,

Аналогичные выражения получатся при дифференцировании по координатам y, z. В итоге

Мы убедились, что исходное центральное поле сил восстанавливается по функции потенциальной энергии:

Рис.4.9. Потенциал гравитационного поля Земли.

Говоря о центральных силах, мы также используем некоторую абстракцию. Что означает силовой центр, к которому (или от которого) направлено поле сил? Мы предполагаем, что центр неподвижен, но реально он образован какими-то физическими телами — зарядами в случае электрического поля, массами — в случае гравитационного. Просто при определенных условиях движением центра можно пренебречь. Скажем, изучая движение спутника вокруг Земли, мы, строго говоря, должны учесть, что спутник и Земля движутся вокруг общего центра масс. Но масса Земли намного превышает массу спутника, центр масс системы практически совпадает с центром Земли, и ее можно считать неподвижным центром гравитационного поля.

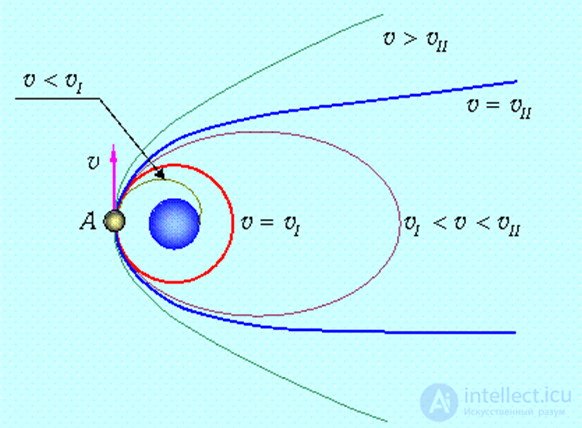
Рис.4.10. Зависимость формы траектории от начальной скорости тела.

Если же такого допущения сделать нельзя, то рассматривают силы взаимодействия между телами. Когда силы направлены вдоль линии, соединяющей тела, а их величина зависит только от взаимного расстояния

мы имеем дело с аналогом центральных сил. Здесь тоже можно ввести потенциальную энергию взаимодействия тел между собой П(r₁₂), так что сила F₁₂ между телами 1 и 2 удовлетворяет соотношению

4.5. закон сохранения энергии

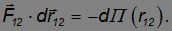
Рассмотрим систему из N материальных точек с массами m₁, m₂, ..., m_N. Предположим, что на точку с номером i действуют: 1) суммарная внутренняя консервативная сила , 2) суммарная внутренняя неконсервативные сила , 3) суммарная внешняя консервативная сила и 4) суммарная внешняя неконсервативная сила . Тогда уравнение движения i-ой точки имеет вид (4.5.1)

(4.5.1)

Умножим обе части уравнения (4.5.1) на элементарное перемещение

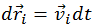
и сложим все уравнения для точек с номерами i = 1, ..., N. При этом учтем, что

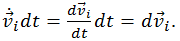
Получим

(4.5.2)

Рассмотрим по отдельности каждый член в этом уравнении. В левой части стоит величина

(4.5.3)

которая с очевидностью является приращением полной кинетической энергии К частиц системы.

Первое слагаемое в правой части (4.5.2) есть суммарная работа всех внутренних консервативных сил. Второе слагаемое есть суммарная работа всех внешних консервативных сил. В силу консервативности сил и то и другое слагаемые можно представить в виде убыли соответствующей потенциальной энергии. В первом случае — внутренние — консервативные силы, в виде убыли потенциальной энергии взаимодействия тел системы:

(4.5.4)

Во втором случае — внешние — консервативные силы, в виде убыли потенциальной энергии системы во внешнем консервативном силовом поле

(4.5.5)

Третье и четвертое слагаемые представляют суммарную работу внутренних и внешних неконсервативных сил и потому не могут быть представлены в виде убыли некоторой скалярной функции только координат по той простой причине, что таковая не существует. Введем для этих слагаемых следующие обозначения: элементарная работа всех внутренних неконсервативных сил

(4.5.6)

и элементарная работа всех внешних неконсервативных сил

(4.5.7)

Перенесем (4.5.4) и (4.5.5) налево и используем обозначения (4.5.6) и (4.5.7), тогда уравнение (4.5.2) приобретет вид.

(4.5.8)

Стоящая в левой части под знаком дифференциала сумма, по определению есть полная механическая энергия системы.

(4.5.9)

Таким образом, окончательно мы получаем соотношение, которое можно назвать теоремой о приращении полной механической энергии:

(4.5.10)

которая гласит: приращение механической энергии системы равно суммарной работе всех неконсервативных сил, как внутренних, так и внешних.

Как следует из (4.5.10), если система замкнута, то приращение ее механической энергии равно работе внутренних неконсервативных сил. То есть одного только факта замкнутости системы (отсутствия внешних сил) недостаточно для того, чтобы механическая энергия сохранялась. Достаточным является полное отсутствие — как среди внешних, так и среди внутренних — неконсервативных сил.

Таким образом, закон сохранения механической энергии гласит:

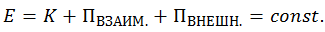
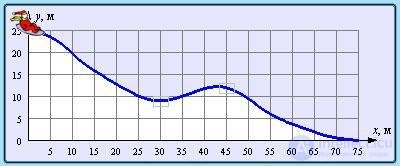
Рис.4.11. Ускорение материальной точки равно нулю в точках экстремумов потенциальной энергии.

Отсюда и название: консервативные (to conserve — беречь, охранять, сберегать, сохранять) силы это такие силы, при действии которых механическая энергия сохраняется/

Закон сохранения механической энергии замкнутой системы можно сформулировать так:

Налицо явное отличие закона сохранения механической энергии замкнутой системы от закона сохранения импульса замкнутой системы: импульс замкнутой системы сохраняется вне зависимости от характера сил, действующих внутри системы, а механическая энергия замкнутой системы сохраняется только тогда, когда внутри замкнутой системы отсутствуют неконсервативные силы. Это легко понять. Механический импульс системы

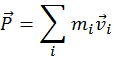
это весь импульс, какой только может быть — другого импульса не существует. А механическая энергия системы (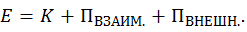) это не вся ее энергия — не учтена внутренняя (тепловая, химическая и т. п.) энергия тел, входящих в состав системы. Неконсервативные силы тем и занимаются, что переводят механическую энергию во внутреннюю, или наоборот, внутреннюю энергию в механическую. Подчеркнем, что механическая энергия замкнутой системы, в результате действия внутри нее неконсервативных сил, может не только убывать, но и возрастать. Например, при взрыве летящего снаряда, суммарная кинетическая энергия его осколков и образовавшихся при взрыве пороховых газов больше, чем кинетическая энергия снаряда (вместе с порохом внутри) непосредственно перед взрывом. Для того, чтобы это было вполне очевидным, перейдем в ту систему отсчета, в которой снаряд непосредственно перед взрывом покоится (в систему его центра масс). Все части снаряда неподвижны, значит полная кинетическая энергия равна нулю. После взрыва осколки снаряда и пороховые газы движутся — кинетическая энергия больше нуля и равна энергии, выделившейся при сгорании пороха.

Закон сохранения энергии является всеобъемлющим постольку, поскольку всеобщим является постулат об однородности времени для замкнутой системы, а общее определение энергии таково: энергия это сохраняющаяся характеристика замкнутой системы, сохранение которой обусловлено однородностью времени. Пока мы — в этом учебнике — имеем дело только с механической энергией, но есть и другие ее формы, в том числе, без сомнения, нам (человечеству) пока неизвестные. Например, совсем недавно астрофизики обнаружили наличие некоторого вида материи, которую назвали «темной материей». На сегодняшний день (начало 2010 года) про нее известно только то, что она подвержена гравитационному притяжению. Если обнаруживается, что в каком-либо физическом процессе энергия не сохраняется, мы ищем новую форму энергии, чтобы обеспечить ее точный баланс. Поступая так, мы вовсе не «жульничаем» и не делаем нечестной попытки скрыть недостаток наших знаний о природе. Так ученые «придумали» тепловую, электромагнитную, ядерную и др. формы энергии. Один из основоположников теории относительности Анри Пуанкаре писал: «Поскольку мы не в состоянии дать общее определение энергии, закон сохранения энергии следует рассматривать просто, как указание на то, что существует «нечто», остающееся постоянным (в любом физическом процессе). К каким бы открытиям ни привели нас будущие эксперименты, мы заранее знаем, что и тогда будет «нечто», обладающее способностью сохраняться, и это нечто мы, скорее всего, сможем называть энергией».

4.6. Условия равновесия механической системы

Закон сохранения энергии позволяет провести анализ общих закономерностей движения, если известна зависимость потенциальной энергии от координат. Рассмотрим для примера одномерное движение материальной точки (частицы), вдоль оси 0x в потенциальном поле, показанном на рис. 4.12.

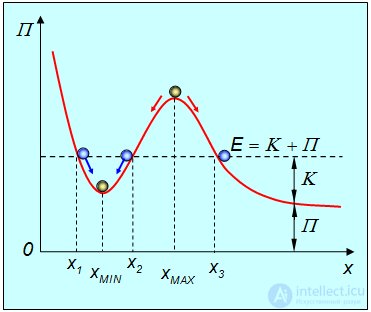
Рис.4.12. Движение частицы вблизи положений устойчивого и неустойчивого равновесия

Поскольку в однородном поле сил тяжести потенциальная энергия пропорциональна высоте подъема тела, можно представить себе ледяную горку (пренебрегаем трением) с профилем, соответствующим функции П(x) на рисунке.

Из закона сохранения энергии E = К + П и из факта, что кинетическая энергия К = Е - П всегда неотрицательна, следует, что частица может находиться лишь в областях, где E > П. На рисунке частица с полной энергией E может двигаться только в областях

В первой области ее движение будет ограничено (финитно): при данном запасе полной энергии частица не может преодолеть «горок» на своем пути (их называют потенциальными барьерами) и обречена вечно оставаться в «долине» между ними. Вечно — с точки зрения классической механики, которую мы сейчас изучаем. В конце курса мы увидим, как квантовая механика помогает частице выбраться из заточения в потенциальной яме — области

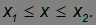
Во второй области движение частицы не ограничено (инфинитно), она может удалиться бесконечно далеко от начала координат направо, но слева ее движение по-прежнему ограничено потенциальным барьером:

Видео 4.6. Демонстрация финитного и инфинитного движений.

В точках экстремума потенциальной энергии x_MIN и x_MAX сила, действующая на частицу, равна нулю, потому что равна нулю производная потенциальной энергии:

Если поместить в эти точки покоящуюся частицу, то она оставалась бы там ... опять-таки вечно, если бы не флуктуации ее положения. В этом мире нет ничего строго покоящегося, частица может испытывать небольшие отклонения (флуктуации) от положения равновесия. При этом, естественно, возникают силы. Если они возвращают частицу к положению равновесия, то такое равновесие называется устойчивым. Если же при отклонении частицы возникающие силы еще дальше уводят ее от равновесного положения, то мы имеем дело с неустойчивым равновесием, и частица в таком положении обычно долго не задерживается. По аналогии с ледяной горкой можно догадаться, что устойчивым будет положение в минимуме потенциальной энергии, а неустойчивым — в максимуме.

Докажем, что это действительно так. Для частицы в точке экстремума x_M (x_MIN или x_MAX) действующая на нее сила F_x(x_M) = 0. Пусть вследствие флуктуации координата частицы изменяется на небольшую величину x. При таком изменении координаты на частицу начнет действовать сила

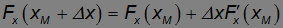
(штрихом обозначена производная по координате x). Учитывая, что F_x=-П', получаем для силы выражение

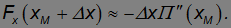
В точке минимума вторая производная потенциальной энергии положительна: U"(x_MIN) > 0. Тогда при положительных отклонениях от положения равновесия x > 0 возникающая сила отрицательна, а при x<0 сила положительна. В обоих случаях сила препятствует изменению координаты частицы, и положение равновесия в минимуме потенциальной энергии устойчиво.

Наоборот, в точке максимума вторая производная отрицательна: U"(x_MAX)<0. Тогда увеличение координаты частицы Δx приводит к возникновению положительной же силы, еще больше увеличивающей отклонение от положения равновесия. При x<0 сила отрицательна, то есть и в этом случае способствует дальнейшему отклонению частицы. Такое положение равновесия неустойчиво.

Таким образом, положение устойчивого равновесия может быть найдено при совместном решении уравнения и неравенства

Видео 4.7. Потенциальные ямы, потенциальные барьеры и равновесие: устойчивое и неустойчивое.

Пример. Потенциальная энергия двухатомной молекулы (например, Н₂ или О₂) описывается выражением вида

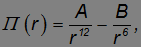
где r — расстояние между атомами, а A, B — положительные постоянные. Определить равновесное расстояние r_М между атомами молекулы. Устойчива ли двухатомная молекула?

Решение. Первый член описывает отталкивание атомов на малых расстояниях (молекула сопротивляется сжатию), второй — притяжение на больших расстояниях (молекула сопротивляется разрыву). В соответствии со сказанным, равновесное расстояние находится при решении уравнения

Дифференцируя потенциальную энергию, получаем

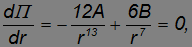
откуда

Находим теперь вторую производную потенциальной энергии

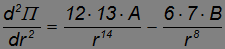
и подставляем туда значение равновесного расстояния r_M :

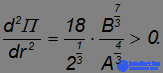
Положение равновесия устойчиво.

На рис. 4.13 представлен опыт по изучению потенциальных кривых и условий равновесия шарика. Если на модели потенциальной кривой поместить шарик на высоту большую высоты потенциального барьера (энергия шарика больше энергии барьера), то шарик преодолевает потенциальный барьер. Если начальная высота шарика меньше высоты барьера, то шарик остается в пределах потенциальной ямы.

Шарик, помещенный в наивысшую точку потенциального барьера, находится в неустойчивом равновесии, поскольку любое внешнее воздействие приводит к переходу шарика в нижнюю точку потенциальной ямы. В нижней точке потенциальной ямы шарик находится в устойчивом равновесии, поскольку любое внешнее воздействие приводит к возвращению шарика в нижнюю точку потенциальной ямы.

Рис. 4.13. Экспериментальное изучение потенциальных кривых

4.7. Примеры применения законов сохранения

Приведем вначале примеры задач-оценок, когда не требуется точного решения, но лишь более или менее адекватная оценка порядков величин.

Пример 1. Гвоздь забили пятью ударами молотка. Оценить, какую силу надо приложить, чтобы выдернуть гвоздь.

Решение. Пусть m — масса молотка, a — его скорость в момент удара. Для оценки можно предположить, что гвоздю передается вся кинетическая энергия молотка. При n ударах эта энергия равна

Энергия гвоздя расходуется на преодоление силы трения F при вхождении гвоздя в стену: при углублении гвоздя на расстояние l совершается работа

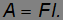
Из равенства A = К находим

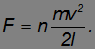
Эта же сила препятствует вытаскиванию гвоздя. Для численной оценки примем разумные исходные данные: m = 1 кг, v = 5 м/с, l = 5 см. Получаем тогда:

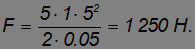
Эта сила примерно эквивалентна весу массы в 130 кг.

При решении мы пренебрегли потерями энергии на нагревание молотка, гвоздя и стенки, но перед нами стояла задача получить всего лишь оценку, а не точное решение.

Пример 2. Оценить мощность выделения тепла при экстренном торможении грузовика.

Решение. Пусть m — масса грузовика, который двигался со скоростью . Кинетическая энергия грузовика до торможения равна

после — нулю. Разность этих кинетических энергий перешла в тепло:

Среднюю скорость грузовика в процессе торможения можно принять равной /2. Если тормозной путь равен l , то до остановки грузовика прошло время

Отсюда находим мощность выделения тепла:

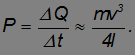
Для численной оценки примем: m = 10 т, v = 72 км/час, l = 20 м. Тогда находим:

Приведем теперь примеры совместного использования законов сохранения импульса и энергии при изучении соударения двух тел. При столкновении тела претерпевают деформацию. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел. Увеличение внутренней энергии тел приводит к повышению их температуры. Существует два предельных типа удара: абсолютно упругий и абсолютно неупругий.

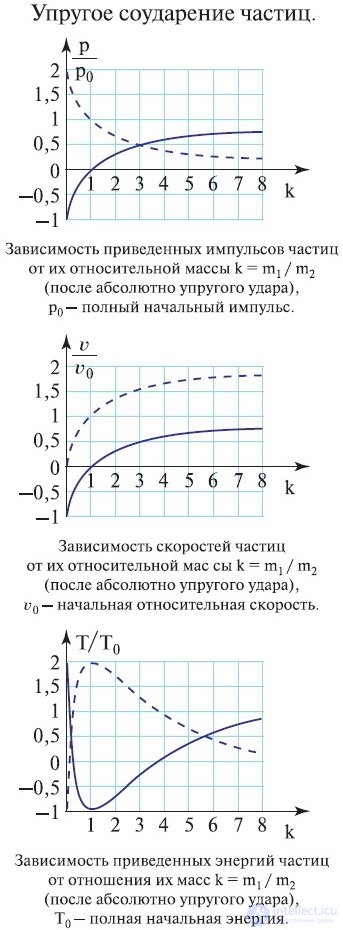
При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга, и разлетаются со скоростями, величина и направление которых определяются двумя условиями — сохранением полной энергии и сохранением полного импульса системы двух тел.

Видео 4.9. Упругое столкновение тележек. «Обмен скоростями» при равенстве масс упруго сталкивающихся тел.

Абсолютно неупругий удар характеризуется тем, что потенциальной энергии упругой деформации не возникает: кинетическая энергия тел полностью или частично превращается во внутреннюю (тепловую) энергию.

При абсолютно неупругом ударе тел работает лишь закон сохранения импульса, механическая энергия не сохраняется, переходит в тепловую (внутреннюю), поэтому имеет место закон сохранения суммарной энергии — механической и внутренней.

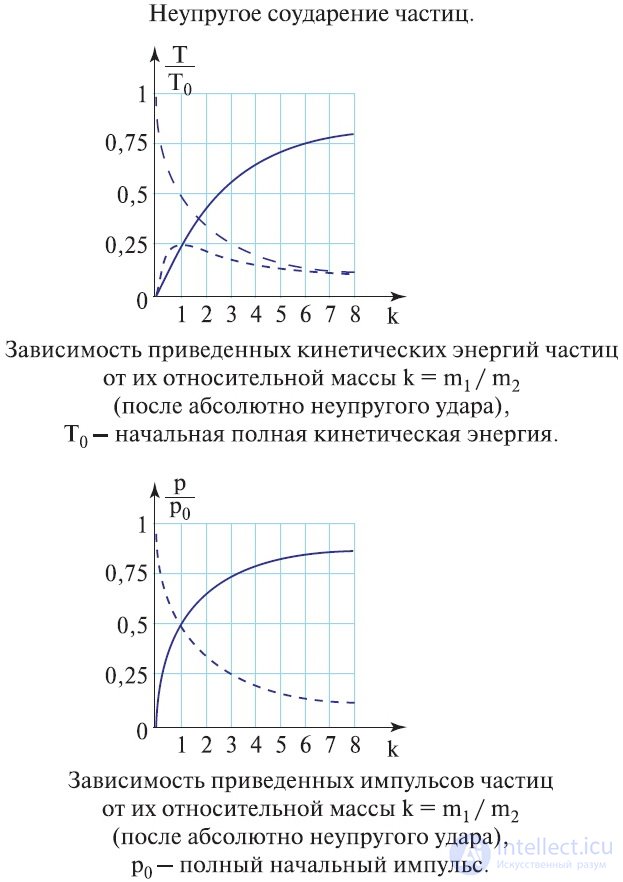
Пусть два сталкивающихся шара образуют замкнутую систему. Рассмотрим сначала абсолютно неупругий удар (рис. 4.16).

Рис. 4.16. Абсолютно неупругое столкновение двух шаров: 1 — состояние до удара; 2 — состояние после удара

Начальные скорости шаров ₁ и ₂, а их массы m₁ и m₂ конечная скорость шаров — . При соударении выполняется закон сохранения импульса:

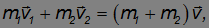
откуда находим скорость образовавшейся составной частицы

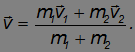
Как и следовало ожидать, соединившиеся шары после соударения продолжают двигаться со скоростью центра масс системы до соударения.

Энергия, перешедшая при этом во внутреннюю энергию шаров, равна разности кинетических энергий до и после соударения:

где 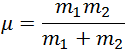— так называемая, «приведенная масса» шаров, а 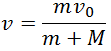— относительная скорость шаров до удара, а именно: скорость до удара второго шара ( 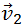минус ) относительно первого. Отсюда видно, что Q равно кинетической энергии относительного движения шаров до удара. Только эта часть полной кинетической энергии шаров до удара может полностью перейти в тепловую (внутреннюю) энергию. Поэтому абсолютно неупругий удар можно определить и так: при абсолютно неупругом ударе вся энергия относительного движения переходит в тепловую (внутреннюю) энергию.

Видео 4.10. Абсолютно неупругое столкновение шаров в системе центра масс и в лабораторной системе отсчета.

Пример 3. Артиллеристы стреляют так, чтобы ядро попало в неприятельский лагерь, находящийся на расстоянии l₀ = 7.2 км от пушки. В момент вылета ядра из дула на него вскакивает барон Мюнхаузен (абсолютно неупругий удар), масса которого в n = 5 раз больше массы ядра. Из-за этого ядро падает, не долетев до цели. Какое расстояние барону придется пройти пешком, чтобы добраться до неприятельского лагеря? Сопротивлением воздуха пренебречь.

Решение. Если ядро вылетело из дула со скоростью ₀, то после вскакивания на него барона его скорость стала равной

где m — масса ядра, а М — масса Мюнхгаузена. Пользуясь формулами темы 2.7, артиллеристы рассчитывали угол возвышения 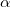орудия по формуле

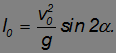
Поскольку скорость изменилась, а угол остался прежним, дальность полета составит

Поэтому барону надо будет пройти расстояние

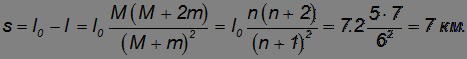
Иными словами, барону удалось пролететь на ядре только 200 м.

Теперь рассмотрим абсолютно упругий удар. Ограничимся случаем центрального удара двух однородных шаров. Удар называется центральным, если векторы скорости центров шаров до удара направлены вдоль прямой, проходящей через центры сталкивающихся шаров (рис. 4.17).

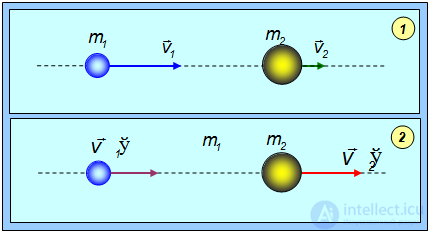
Рис. 4.17. Абсолютно упругое центральное соударение двух шаров: 1 – состояние до удара; 2 – состояние после удара

Шары рассматриваем как материальные точки, то есть пренебрегаем их возможным вращением. Как и в предыдущем случае, пренебрежем также трением о поверхность, по которой движутся шары. Напишем уравнения сохранения механической энергии и импульса.

В рассматриваемом случае центрального удара скорости шаров после удара будут направлены вдоль той же прямой, по которой двигались центры шаров перед ударом. Поэтому векторы скоростей можно заменить их проекциями на линию соударения:

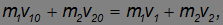
где m₁ и m₂ — массы шаров, v₁₀ и v₂₀ — скорости шаров до удара и v₁ и v₂ — скорости шаров после удара (скорости понимаются в алгебраическом смысле: знак указывает направление движения вдоль линии соударения).

Преобразуем уравнения сохранения энергии и импульса к виду:

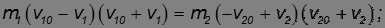
Выражения, стоящие в левой и правой частях уравнений, будем считать отличными от нуля (иначе v₁₀ = v₁ и v₂₀ = v₂ — скорости шаров не изменились, то есть столкновения не произошло). Разделим первое уравнение на второе, после чего получим:

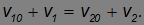
Умножим полученное уравнение на m₂ и вычтем из него преобразованное уравнение закона сохранения импульса. Находим:

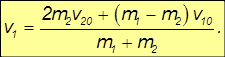
Аналогично умножим полученное уравнение на m₁ и сложим с ним преобразованное уравнение закона сохранения импульса. Получим:

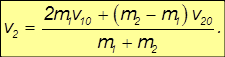
В отличие от неупругого столкновения, здесь скорости шаров после соударения не могут быть равны. В самом деле, если v₁ = v₂, то из полученных выражений для скоростей шаров после удара следует, что до соударения скорости тоже были равны v₁₀ = v₂₀. Но в этом случае соударение не может произойти. При центральном ударе шары столкнутся, если они движутся навстречу друг другу или один шар догоняет другой.

Анализ полученных соотношений

1. Если второй шар первоначально покоился (v₂₀ = 0), то после соударения скорости шаров определяются соотношениями

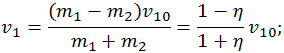
Здесь η = m₂/m₁ — отношение масс сталкивающихся шаров. Отметим, что при заданной скорости налетающего шара до столкновения, скорости шаров после столкновения определяются исключительно отношением масс шаров.

Знак скорости v₂ совпадает со знаком v₁₀: покоившийся шар обязательно начнет двигаться в направлении движения налетающего шара. Знак скорости v₁ зависит от соотношения масс шаров: если покоившийся шар более массивен, то налетавший отскочит в обратном направлении, если более массивен налетающий шар, он продолжит движение в том же направлении. При равенстве масс налетающий шар остановится.

Рассмотрим два предельных случая:

• Масса покоящегося шара гораздо больше массы налетающего: m₂ >> m₁ или η>>1.

  Тогда

  

  (то есть тяжелый шар остается неподвижным) и

  

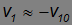
  (легкий шар отскакивает с той же скоростью в обратном направлении).

• Масса налетающего шара намного превосходит массу покоящегося: m₁>>m₂ или η<<1.

  Тогда

  

  (тяжелый шар не меняет своей скорости) и

  

2. Если массы шаров равны (m₁ = m₂ или η=1), то из полученных формул для скоростей шаров после столкновения следует

то есть шары при соударении обмениваются скоростями. С частным случаем этого явления мы познакомились выше: до соударения покоился шар 2, после — шар 1.

3. Если оба шара двигаются, но масса одного шара много больше массы другого (m₂>>m₁), то

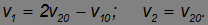
Иначе говоря, массивный шар не "замечает" соударения с легким шаром и продолжает двигаться с прежней скоростью. Скорость же легкого шара меняется. Мы получили комбинацию полученных ранее результатов.

Законы столкновения шаров иллюстрируются с помощью интерактивной компьютерной модели (рис. 4.18).

Рис. 4.18. Исследование законов столкновения шаров с помощью интерактивной компьютерной модели

Пусть имеется ряд одинаковых соприкасающихся упругих шаров. С крайним шаром ряда сталкивается такой же шар, движущийся со скоростью v₀ (рис. 4.19). В результате удара он останавливается, а последний шар ряда начинает двигаться с той же скоростью v₀.

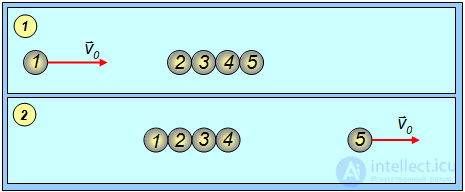
Рис 4.19. Упругое столкновение шара с несколькими покоящимися шарами: 1 – положение до соударения; 2 – после соударения

Это явление объясняется тем, что при столкновении шаров 1 и 2 шар 1 останавливается, а шар 2 приобретает скорость v₀. Шар 2 тут же сталкивается с шаром 3 и останавливается и т. д.

Пусть на неподвижный ряд одинаковых шаров налетают два таких же шара, движущихся со скоростью v₀ каждый (рис. 4.20).

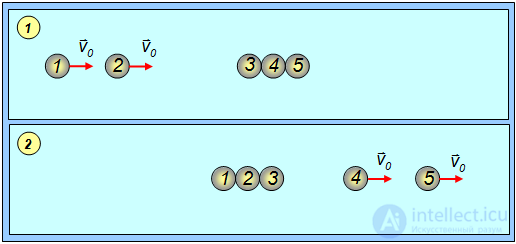
Рис 4.20. Упругое столкновение двух шаров с несколькими покоящимися шарами: 1 – положение до соударения; 2 – после соударения.

Сначала при столкновении шара 2 с шаром 3, шар 2 останавливается, а шар 3 приобретает скорость v₀, передавая ее шару 4 и т. д. Сразу же после этого шар 1 сталкивается с шаром 2, останавливается, передавая свою скорость шару 2, и процесс повторяется. В результате все шары, кроме двух последних, движущихся со скоростями v₀, остаются неподвижными.

Центральные упругие столкновения в цепочке одинаковых шаров демонстрируются на рис. 4.21.

Рис. 4.21. Центральные столкновения в цепочке одинаковых шаров

Здесь все шары подвешены на длинных нитях, и задача сводится к изучению их попарных столкновений. При этом крайние шары будут поочередно отскакивать с одинаковой скоростью и отклоняться на нитях на одинаковые углы, а все остальные шары, находящиеся между ними, будут находиться в состоянии покоя.

Видео 4.11. Нецентральное упругое столкновение шаров одинаковой массы. Эффект вращения шаров после удара.

Знакомство с конкретными примерами позволяет сформулировать общие важные положения. Не все из них вытекают, правда, из вышесказанного, но это и не удивительно: само понятие энергии гораздо шире его проявления в механике, и мы только начинаем с ним знакомиться. Итак:

• Законы сохранения носят фундаментальный характер и тесно связаны с симметрией пространства и времени. Закон сохранения энергии связан с однородностью времени, то есть равнозначностью всех моментов времени. Закон сохранения импульса связан с однородностью пространства, то есть равнозначностью всех точек пространства.
• Законы сохранения носят общий характер и не зависят от конкретной системы и ее движения. Из законов сохранения вытекает, что какие-то процессы заведомо оказываются невозможными. Так, в 1775 г. Французская Академия решила не принимать к рассмотрению проекты вечных двигателей как противоречащих закону сохранения энергии.
• Законы сохранения позволяют рассмотреть общие свойства движения без решения уравнений и детальной информации о протекании процессов во времени. Поэтому законы сохранения могут быть использованы даже в тех случаях, когда силы точно не известны. Так, в частности, обстоит дело в физике элементарных частиц. Даже в тех случаях, когда силы заданы в точности, законы сохранения могут оказать существенную помощь при решении задач о движении частиц.

4.8. закон сохранения момента импульса

Мы уже говорили, что законы сохранения энергии и импульса связаны с однородностью времени и пространства, соответственно. Но у трехмерного пространства, в отличие от одномерного времени, имеется еще одна симметрия. Пространство изотропно, в нем нет выделенных направлений. С этой симметрией связан закон сохранения момента импульса. Эта связь проявится в том, что момент количества движения, как мы увидим в дальнейшем, является одной из основных величин, описывающих вращательное движение.

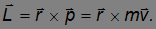
Направление вектора L определяется по правилу буравчика (штопора), а его величина равна

где 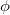— угол между векторами r и р. Величина l = r 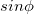равна расстоянию от начала координат 0 до прямой, вдоль которой направлен импульс частицы. Эта величина называется плечом импульса (рис. 4.22). Вектор L зависит от выбора начала координат, поэтому говоря о нем, обычно указывают: «момент импульса относительно точки 0».

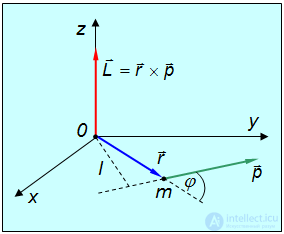
Рис. 4.22. Момент импульса L частицы массой m

Рассмотрим производную по времени от момента импульса:

Первое слагаемое равно нулю, так как и 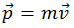очевидным образом параллельны

Во втором слагаемом, согласно второму закону Ньютона, производную импульса можно заменить на силу, действующую на частицу.

Направление момента силы определяется тем же правилом буравчика. Его величина

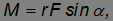
где 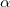— угол между радиус-вектором и силой. Аналогично тому, как это было сделано выше, определяется и плечо силы l = r 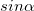— расстояние от точки 0 до линии действия силы. В итоге из полученного в результате дифференцирования соотношения находим уравнение движения для момента импульса частицы:

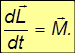
По форме уравнение аналогично второму закону Ньютона: вместо импульса частицы стоит момент импульса, а вместо силы — момент силы.

Если M = 0, то L = const, то есть

Для центральных сил

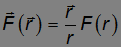
и момент силы относительно силового центра равен нулю:

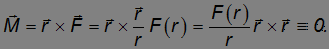
Таким образом, для центральных сил

то есть L = const.

Другими словами,

Отсюда вытекает важное следствие. Поскольку момент импульса ортогонален плоскости, задаваемой импульсом тела и радиус-вектором, проведенным из центра сил, эта плоскость не меняет своего положения со временем. Иными словами, орбита каждого тела в поле центральных сил лежит в одной плоскости, проходящей через центр сил (хотя для разных тел эти плоскости могут различаться). Таким образом, в поле центральных сил невозможны, например, винтовые траектории.

Рассмотрим теперь систему, состоящую из двух взаимодействующих частиц (рис. 4.23).

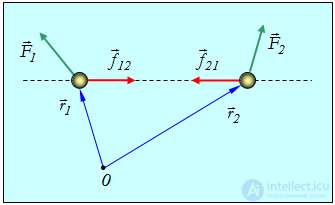
Рис. 4.23. Система, состоящая из двух взаимодействующих частиц

Уравнения движения этих частиц имеют вид:

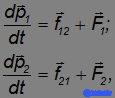
где F₁ и F₂ — внешние силы, a f₁₂=-f₂₁ — внутренние силы взаимодействия между частицами, направленные вдоль линии, их соединяющей

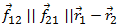
Умножим первое уравнение векторно слева на радиус-вектор первой частицы r₁, а второе — векторно слева на радиус-вектор второй частицы r₂

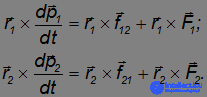
Учтем, что

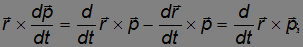
поскольку

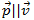
и

Используя третий закон Ньютона f₁₂ = –f₂₁, перепишем систему уравнений движения частиц в виде:

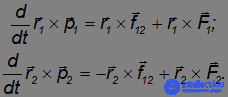
Сложим полученные соотношения:

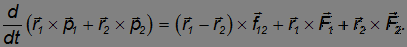
Имеет место соотношение между векторами

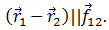
Поэтому их векторное произведение равно нулю.

Таким образом, мы получаем

В левой части равенства стоит производная от суммы моментов импульса частиц (ее называют полным моментом импульса L системы), а в правой — сумма моментов внешних сил — полный момент М внешних сил, действующих на тела системы. Обобщение на случай системы из многих частиц (или твердого тела) очевидно.

Момент импульса системы N частиц равен

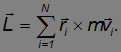
Полный момент внешних сил будет

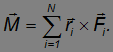
Уравнение, определяющее изменение во времени момента импульса системы частиц имеет вид:

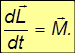
Отсюда следует, что при М = 0 и, соответственно, L = const следует закон сохранения момента импульса системы:

Пример. Выясним, при каких условиях момент импульса системы не зависит от выбора начала координат 0.

Найдем сначала, как изменяется момент импульса при смене начала координат. Возьмем некую точку 0', положение которой относительно точки 0 задается радиус-вектором r₀. Радиус-векторы r_i', проведенные из 0', связаны с радиус-векторами r_i соотношениями

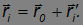
Подставим это выражение в формулу для момента импульса L относительно точки 0 :

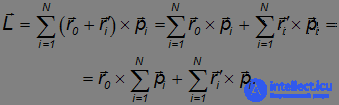
В первом члене мы введем полный импульс системы

а второй член есть не что иное, как момент импульса L' относительно точки 0'.

Имеем

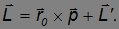
Мы ищем условие, когда

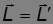
для произвольного вектора r₀. Это возможно только при равенстве нулю полного импульса системы р = 0. Иными словами, момент импульса не зависит от выбора начала координат в системе отсчета, связанной с центром масс системы.

4.9. Движение частицы в центральном силовом поле

Рассмотрим более подробно движение частицы в центральном силовом поле. Как уже отмечалось выше, ее момент импульса относительно силового центра сохраняется

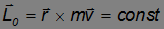
или в скалярной форме

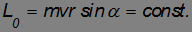
Пусть перемещение частицы за время dt есть vdt. Площадь, «заметаемая» радиус-вектором частицы (заштрихована на рис. 4.24) за это время, будет

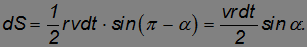
Рис. 4.24. Cекториальная скорость частицы

Подставляя выражение для площади в формулу для секториальной скорости, получим

Учитывая, что

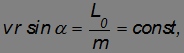
приходим к закону площадей.

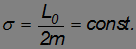
Пример. Пусть спутник движется вокруг Земли по эллиптической орбите (рис. 4.25), причем минимальное и максимальное удаление от Земли составляет R_min и R_max. Найдем его скорость в перигее и апогее.

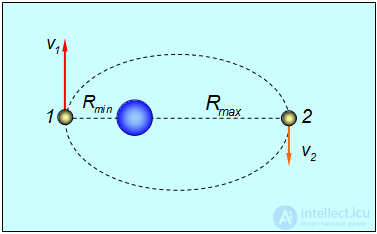
Рис. 4.25. Движение спутника по эллиптической орбите вокруг Земли

Запишем в точках 1 и 2 закон сохранения момента импульса для спутника:

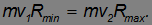
Запишем для тех же точек закон сохранения энергии:

Выражая v₂ из закона сохранения момента импульса

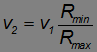
и подставляя полученное выражение в закон сохранения энергии, находим искомые скорости

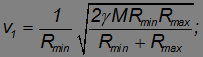
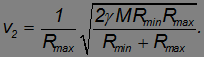
Видно, что в точке минимального удаления скорость спутника максимальна, и, наоборот, в точке максимального удаления его скорость минимальна.

Исследование, описанное в статье про закон сохранения энергии, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое закон сохранения энергии, закон сохранения момента импульса, работа силы, равновесие механической системы, применение законов сохранения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики