2.2. Угловая скорость кратко

Сразу хочу сказать, что здесь никакой воды про угловая скорость, и только нужная информация. Для того чтобы лучше понимать что такое угловая скорость , настоятельно рекомендую прочитать все из категории Физические основы механики.

угловая скорость — векторная величина, характеризующая быстроту и направление вращения материальной точки или абсолютно твердого тела относительно центра вращения. Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта. Строго говоря, угловая скорость представляется псевдовектором (аксиальным вектором), и может быть также представлена в виде кососимметрического тензора .

Векторная величина

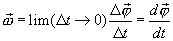(2.1)

называется угловой скоростью тела. Вектор 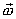направлен вдоль мгновенной оси вращения в сторону, определяемую правилом винта, т.е. также как вектор элементарного поворота 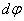. Модуль вектора угловой скорости равен 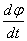. Вращение с постоянной угловой скоростью называется равномерным, при этом:

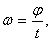
т.е. при равномерном вращении 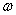показывает, на какой угол поворачивается тело за единицу времени.

Характеристика быстроты вращения тела вокруг неподвижной оси => угловая скорость:

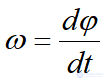
Размерность в системе СИ – радиан/сек или 1/сек.

Движение по окружности данного радиуса R, будет задано в том случае, если заданы

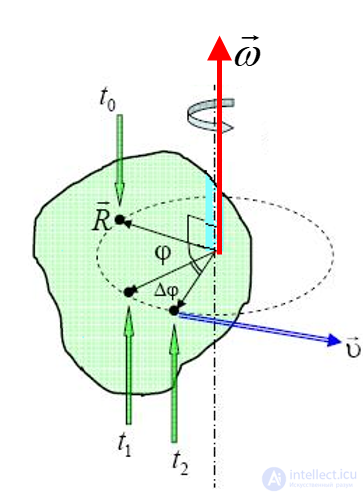
1. величина угловой скорости ω,

2. плоскость в которой лежит окружность,

3. направление вращения

Все три характеристики могут быть даны с помощью одного вектора:

Вектор перпендикулярен плоскости вращения

Направление вектора дает направление вращения по правилу правого винта.

Будем считать, что ω – это такой вектор

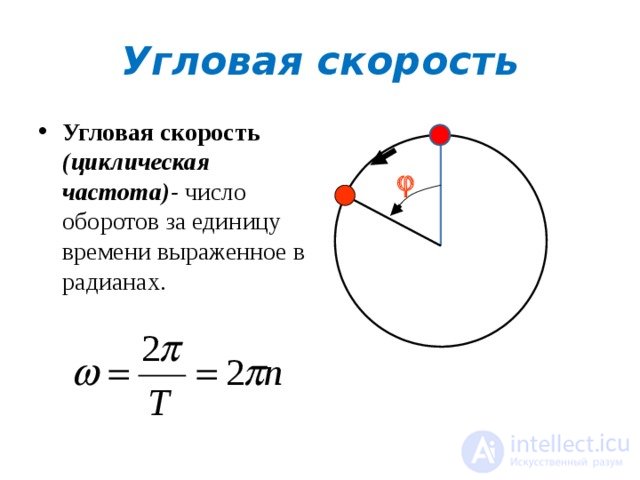
При вращении с постоянной угловой скоростью полный оборот совершается за время

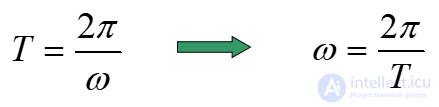
Величина обратная периоду – число оборотов в единицу времени:

Т и ν можно рассматривать и как характеристики движения с переменной угловой скоростью. Тогда они будут характеризовать вращение в данный момент времени.

Пример: изменение скорости вращения ротора, двигателя и т.п. характеризуют изменением числа оборотов (а не изменением угловой скорости).

Векторное представление в трехмерном пространстве

В трехмерном пространстве вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения за единицу времени:

а направлен по оси вращения согласно правилу буравчика, то есть в ту сторону, в которую ввинчивался бы буравчик или винт с правой резьбой, если бы вращался в эту сторону. Другой мнемонический подход для запоминания взаимной связи между направлением вращения и направлением вектора угловой скорости состоит в том, что для условного наблюдателя, находящегося на конце вектора угловой скорости, выходящего из центра вращения, само вращение выглядит происходящим против часовой стрелки.

Угловая скорость является аксиальным вектором (псевдовектором). При отражении осей системы координат компоненты обычного вектора (например, радиус-вектора точки) меняют знак. В то же время компоненты псевдовектора (в частности, угловой скорости) при таком преобразовании координат остаются прежними.

Тензорное представление

Вектор угловой скорости определенное выше, может быть эквивалентно выражено как тензор угловой скорости , матрица (или линейное отображение) W = W ( t ), определяемая следующим образом:

Это бесконечно малая матрица вращения . Линейное отображение W действует как :

Единицы измерения

Единица измерения угловой скорости, принятая в Международной системе единиц (СИ) и в системах СГС и МКГСС, — радиан в секунду (русское обозначение: рад/с, международное: rad/s) ^{[Комм 1]}. Об этом говорит сайт https://intellect.icu . В технике также используются обороты в секунду, намного реже — градусы, минуты, секунды дуги в секунду, грады в секунду. Часто в технике используют обороты в минуту — это идет с тех времен, когда частоту вращения тихоходных паровых машин определяли просто на глаз, подсчитывая число оборотов за единицу времени.

Свойства

Вектор мгновенной скорости любой точки абсолютно твердого тела, вращающегося с угловой скоростью , определяется формулой:

где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы измерения углов, то в двух последних формулах появится множитель, не равный единице.

• В случае плоского вращения, то есть когда все векторы скоростей точек тела всегда лежат в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось вращения, то есть на прямую, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается. Однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
• Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю). Равномерное вращение является частным случаем плоского вращения.
• Производная угловой скорости по времени есть угловое ускорение.
• Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, отличающихся положением начала отсчета и скоростью его движения, но двигающихся равномерно прямолинейно и поступательно друг относительно друга. Однако в этих инерциальных системах отсчета может различаться положение оси или центра вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
• В случае движения точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

где — радиус-вектор точки (из начала координат), — скорость этой точки, — векторное произведение, — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы подходящие по определению, по-другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твердого тела вектора угловой скорости вращения всех его точек совпадают). Однако в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

• В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) абсолютно твердого тела декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.

• При измерении угловой скорости в оборотах в секунду (об/с) модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости численно связан с частотой вращения так: Наконец, при использовании градусов в секунду численная связь с частотой вращения будет:

Связь с конечным поворотом в пространстве

• Пусть поворот, изменяющийся во времени, задан величиной угла и ортом оси конечного поворота в пространстве Тогда угловая скорость, соответствующая этому повороту, равна

• Если поворот задан матрицей поворота где — символ Кронекера, — символ Леви-Чивиты (суммирование ведется по правилу Эйнштейна от 1 до 3), выражение для элементов которой через и могут быть получены, например, с помощью формулы Родрига, то угловая скорость равна

• Если для описания поворота используется кватернион, выражаемый через угол и орт оси поворота как то угловая скорость находится из выражения

• В случае, когда поворот описывается с помощью вектора изменяющегося во времени, обозначим а также — матрица половинного поворота — квадрат модуля вектора Тогда угловая скорость:

Вау!! 😲 Ты еще не читал? Это зря!

• кинематика вращательного движения , абсолютно твердое тело ,
• угол поворота твердого тела ,
• период обращения , частота обращения ,
• угловое ускорение ,
• кинематика , вращение абсолютно твердого тела ,
• Угловой момент
• Ареальная скорость
• Изометрия
• Ортогональная группа
• Динамика жесткого тела
• Завихренность

Статью про угловая скорость я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое угловая скорость и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики

Из статьи мы узнали кратко, но содержательно про угловая скорость