Лекция
Привет, Вы узнаете о том , что такое специальная теория относительности, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое специальная теория относительности, преобразования галилея, преобразования лоренца, постулаты эйнштейна, сложение скоростей в релятивистской механике, аберрация света, частицы с нулевой массой , настоятельно рекомендую прочитать все из категории Физические основы механики.
Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедливы законы динамики Ньютона, то эти системы являются инерциальными. Г. Галилей установил, что во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму: в этом заключается суть механического принципа относительности (принципа относительности Галилея). Создание в XIX веке электродинамики Фарадея — Максвелла и многочисленные опыты с электрическими и магнитными полями, привели ученых (цитируя Эйнштейна) «к предположению, что не только в механике, но и в электродинамике никакие свойства явлений не соответствуют понятию абсолютного покоя, и даже более того — к предположению, что для всех координатных систем, для которых справедливы уравнения механики, имеют место те же самые электродинамические и оптические законы...» Однако, отмечал Эйнштейн, «электродинамика Максвелла в том виде, как ее в настоящее время обыкновенно понимают, в применении к движущимся телам приводит к асимметрии, которая, по-видимому, несвойственна самим явлениям». Разрешение этого противоречия между обобщением принципа относительности и уравнениями электродинамики привело к отказу от преобразований Галилея и созданию специальной теории относительности (СТО), являющейся предметом этой главы.
Рассмотрим две системы отсчета — инерциальную систему K (с координатами x, y, z ), которую условно будем считать неподвижной, и систему K' (с координатами x', y', z' ), движущуюся относительно K равномерно и прямолинейно со скоростью v (для конкретности вдоль оси x ). Отсчет времени начнем с момента, когда начала координат обеих систем совпадают (рис. 6.1).
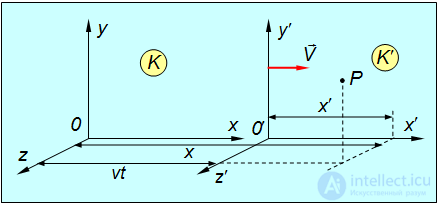
Рис. 6.1. преобразования галилея при переходе из одной инерциальной системы отсчета в другую
Ранее мы уже нашли связь между координатами произвольной точки P в обеих системах отсчета:
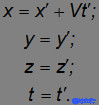
Эти уравнения носят название преобразований Галилея. В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета, то есть к преобразованиям координат мы добавили еще и уравнение совпадения времен.
Продифференцировав преобразования Галилея по времени с учетом

мы получаем правило сложения скоростей по Галилею в векторной форме:
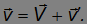
Дифференцируя еще раз, находим соотношение для ускорений — ускорение a в системе К оказывается равным ускорению а' в системе К' :
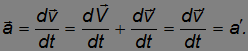
Еще раз: ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно (то есть V = const), оказывается одним и тем же. Как говорят, ускорения инвариантны относительно таких систем отсчета. Поэтому, если одна из них инерциальная, то и остальные системы отсчета также будут инерциальными.
Как следствие, никакими механическими опытами невозможно установить, покоится данная система отсчета или движется прямолинейно и равномерно. Иными словами, в природе отсутствует выделенная система отсчета.
Величины, численные значения которых не изменяются при преобразованиях координат, называются инвариантами преобразований.
Инвариантность длины и интервала времени. Расстояние между двумя точками P1 и P2 можно выразить через координаты этих точек в системе К :
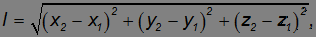
и именно это расстояние измеряет наблюдатель в системе отсчета К. Для наблюдателя же в системе отсчета К' координаты тех же точек будут другими, и он определит расстояние между ними как
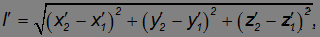
Из преобразований Галилея следует, что
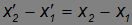
и аналогично для других координат, так что
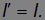
Иными словами, оба наблюдателя находят одно и то же значение для расстояния между двумя точками — длина инвариантна по отношению к преобразованиям Галилея.
Аналогичным образом, очевидно, инвариантны интервалы времени для обоих наблюдателей:
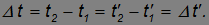
Если два события одновременны (t1 = t2), то временной интервал между ними равен нулю. Вследствие инвариантности это же справедливо и в системе отсчета К', то есть данные события одновременны в любой инерциальной системе отсчета.
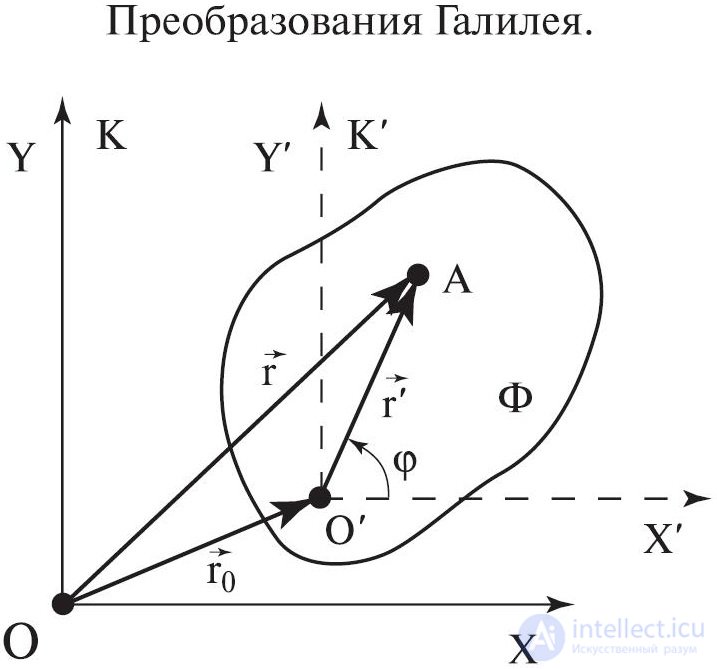
Рис. 6.2. Преобразования Галилея в общем случае
Задумаемся, откуда взялись столь естественные на первый взгляд утверждения? Преобразования Галилея для координат следуют из простого геометрического правила сложения векторов. Но посмотрим на этот рисунок внимательнее. Вектор r' в сущности задан относительно системы К', наблюдатель в этой системе описывает им положение некоторой точки в пространстве. Наблюдатель в системе отсчета К предполагает, что может использовать этот же радиус-вектор, чтобы сложить с радиус-вектором начала отсчета 0' и получить положение той же точки относительно системы К. Но на чем основано это предположение? На том, что вектор r' одинаков в обеих системах отсчета, что у него в обеих системах те же проекции на координатные оси и та же длина. А это значит, что при выводе преобразования Галилея мы изначально неявно предположили инвариантность расстояний. Инвариантность же интервалов времени мы постулировали совершенно откровенно. Основанием для этого служит наш повседневный опыт. Но любой опыт ограничен какими-то масштабами, в пределах которых он приобретен. Когда ученые столкнулись с физикой больших скоростей при изучении распространения электромагнитных волн (света) оказалось, что наш повседневный опыт более не применим.
Рассмотрим сначала другой волновой процесс — звук. Звук распространяется в упругой среде: воздухе, воде, твердых телах. Скорость звука определяется свойствами среды и постоянна относительно среды. Если наблюдатель движется в среде, то относительно него скорость звука будет другой, и определяется она законом сложения скоростей Галилея. При наличии среды о принципе относительности говорить не приходится: выделена та система отсчета, в которой среда покоится. Движение всех остальных систем отсчета легко установить (например, при движении автомобиля наличие воздушной среды обнаруживается по сопротивлению воздуха — кажущемуся ветру).
Раньше думали, что свет — это также механический волновой процесс в особой упругой среде, названной эфиром. Относительно эфира свет распространяется со скоростью, которую принято обозначать буквой с.
Экспериментально установлено, что скорость света равна c = 2,998·108 м/с = 299,8 тыс. км/с. Механический принцип относительности Галилея означает, что при механическом движении эфирного ветра не наблюдается. Это объясняли «тонкостью», «разреженностью» эфира, не оказывающего сопротивления движению «грубых» объектов, с которыми имеет дело механика. Иное дело — электромагнитные явления, распространение света. Там эфирный ветер должен был наблюдаться, и цель опытов (Майкельсон, 1881; Майкельсон и Морли, 1887) как раз и заключалась в поисках этого ветра.
Идея состояла в использовании орбитального движения Земли со скоростью V = 30 км/c. При движении с этой скоростью относительно эфира наблюдатель мог бы обнаружить видимое изменение скорости света: она должна быть равна c + V при движении навстречу световому лучу и c – V при удалении от источника света. Отношение скоростей Земли и света
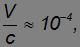
так что надо было добиться такой или более высокой относительной точности измерений. Это оказалось возможным благодаря использованию интерферометра. Мы не станем вдаваться в технические подробности опыта Майкельсона — Морли, но расскажем лишь о его основной физической идее.
В этом опыте сравнивались времена прохождения света от источника S к зеркалу M и обратно к источнику для двух случаев: когда путь света был параллелен и ортогонален орбитальной скорости Земли.
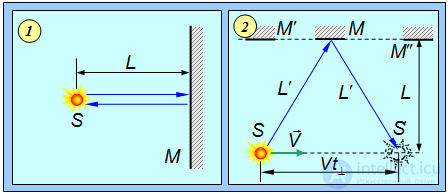
Рис. 6.3. Идея опыта Майкельсона — Морли: 1 — путь света параллелен орбитальной скорости Земли; 2 — путь света ортогонален орбитальной скорости Земли
В первом случае (см. рис. 6.3–1) свет проходит путь L до зеркала за время
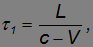
a обратный путь — за время
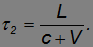
Складывая эти времена, получаем полное время, затрачиваемое светом на прохождение пути до зеркала и обратно:
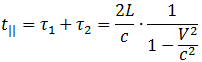
Во втором случае (см. рис. 6.3–2) из-за движения зеркала и источника свет затратит на путь время
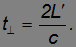
Расстояние L' легко найти по теореме Пифагора:
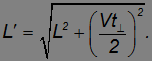
откуда получаем уравнение для времени, за которое свет проходит свой путь вот втором случае
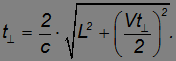
Решение этого уравнения дает
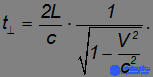
Сравнивая времена распространения света в первом и втором случаях, убеждаемся, что они различаются
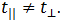
Конструктивно интерферометр Майкельсона был выполнен так, что луч от источника раздваивался, часть его шла параллельно скорости Земли, а часть — ортогонально. После отражения от зеркал лучи встречались в одной точке и создавали интерференционную картину (рис. 6.4).
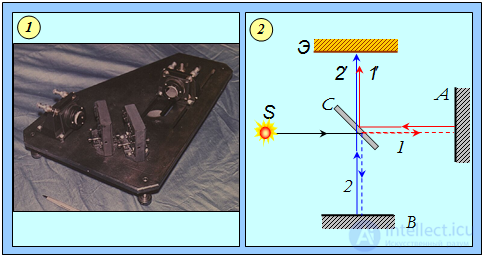
Рис. 6.4. Интерферометр Майкельсона: 1 — общий вид; 2 — схема установки
Никакой разницы во временах прохождения обоих путей обнаружено не было. Но, быть может, скорости Земли и эфира случайно совпали, и потому эфирного ветра не наблюдалось? Опыт повторили через полгода, когда Земля в своем орбитальном движении повернула в противоположную сторону. Результат оказался тем же.
Для объяснения отрицательного результат опыта Майкельсона — Морли была выдвинута интересная гипотеза. Сначала Дж. Фитцджеральд, а затем (независимо от него) Г.А. Лоренц попытались объяснить результат опыта тем, что эфирный ветер «давит» на тела и сокращает их размеры вдоль направления движения. Если это так, то в формулах для продольного распространения света в интерферометре надо заменить «истинную» длину пути L на некоторую другую величину L||. Тогда формула для определения времени, затрачиваемого светом при распространении в направлении, параллельном орбитальной скорости Земли, примет вид
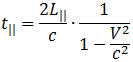
Для совпадения времен
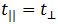
достаточно тогда положить
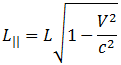
Гипотеза Лоренца — Фитцджеральда казалась искусственной, изобретенной только для объяснения результатов одного эксперимента.
А между тем у физиков появилась еще одна трудность, не связанная с опытом Майкельсона — Морли. К этому времени сформировалась теория электромагнетизма, воплотившаяся в уравнения Максвелла. И оказалось, что уравнения Максвелла не инвариантны относительно преобразований Галилея. Это означало, что с помощью электромагнитного поля, казалось бы, можно сделать то, что не удалось в опытах Майкельсона — обнаружить движение инерциальной системы. Но тогда пришлось бы отказаться от принципа относительности Галилея, который выглядел весьма убедительно. К тому же свет, использованный в опытах Майкельсона-Морли, это частный случай электромагнитного поля.
Поэтому был поставлен вопрос: а как должны выглядеть преобразования координат от одной системы отсчета к другой, чтобы уравнения Максвелла были инвариантными? Ответ дал в 1904 г. Лоренц, и с тех пор эти преобразования называют его именем (хотя они появлялись ранее в работах других ученых — у В. Фохта в 1887 г. и у Дж. Лармора в 1900 г.).
Из уравнений Максвелла следует, в частности, что свет распространяется со скоростью c. Вернемся снова к двум инерциальным системам отсчета (см. рис. 6.1). Одну мы будем считать неподвижной (К-система). Пусть другая (К'-система) движется относительно К-системы с постоянной скоростью V. Для упрощения будем считать, что оси координат обеих систем параллельны, в начальный момент времени начала отсчета 0 и 0' совпадают, а затем точка 0' движется со скоростью V вдоль оси x. Пусть в начальный момент времени t = 0 из точки 0 (совпадающей с точкой 0' ) вдоль оси х излучается световой импульс. Уравнение его движения имеет вид
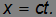
Таким же должно быть и его уравнение движения относительно системы отсчета К' :
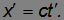
Это — частный случай инвариантности уравнений Максвелла, но его рассмотрения достаточно, чтобы вывести преобразования Лоренца.
Мы будем рассуждать так же, как и при выводе преобразований Галилея, учитывая все, что успели с тех пор узнать. При преобразованиях Галилея координата x относительно системы отсчета K складывалась из положения начала отсчета системы K' (величина Vt) и координаты x'. Но сейчас мы уже не будем предполагать инвариантности длин и потому умножим x' на некий коэффициент γ. Иными словами, мы предполагаем пропорциональность длин в разных системах отсчета, но не их равенство. Тогда координата x какой-либо материальной точки связана с координатой x' этой же точки соотношением
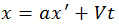
Коэффициент γ пока неизвестен, а отрезок Vt — расстояние между точками 0 и 0' в момент времени t, измеряемый по часам системы K.
Если система K' движется относительно K со скоростью V, то система K движется относительно K' со скоростью –V. Ввиду равноправности обеих систем отсчета можно написать аналогичную связь между координатами:

Теперь отрезок Vt' — это расстояние между точками 0 и 0' в момент времени t', измеряемый по часам системы K'. Как видно, мы не предполагаем инвариантности интервалов времени, но и не отвергаем такую возможность: если наши уравнения допустят решение
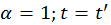
то мы вернемся в лоно классической механики. Как мы увидим, этот вариант не реализуется.
Запишем прямые и обратные преобразования координат так, чтобы в левой и правой частях уравнений стояли координаты и времена, относящиеся к одной системе отсчета. Для этого выразим x через x', t' с помощью второго уравнения, подставим это выражение в первое уравнение и найдем оттуда t. Получаем в итоге:
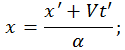
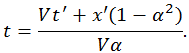
Применим теперь полученные преобразования координат и времени к законам движения светового импульса в системе отсчета K. Подставим найденные выражения для x, t в уравнение движения светового импульса
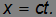
Получим
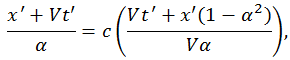
откуда
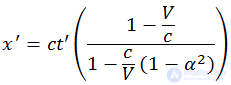
Чтобы это уравнение имело вид
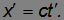
выражение в скобках должно быть равно единице, то есть
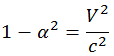
или
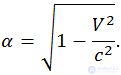
Подставляя выражение для γ в найденные выше преобразования координат и времени, получаем преобразования Лоренца. Их надо дополнить соотношениями
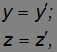
которые в точности совпадают с тем, что было в преобразованиях Галилея. Для получения обратных преобразований достаточно поменять знак у скорости V.
Величину
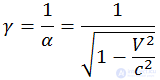
общепринято называть релятивистским фактором (множителем). С учетом этого обозначения преобразования Лоренца, оставляющие инвариантными уравнения теории электромагнетизма, имеют вид:
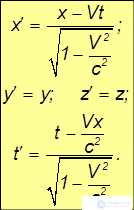
Обратные преобразования Лоренца имеют вид:
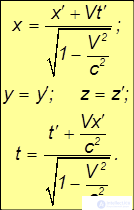
Видно, что в отличие от преобразований Галилея, здесь преобразуются не только пространственные координаты, но и время.
Достижения предшественников были осмыслены и приведены в стройную систему благодаря работам А. Пуанкаре и А. Эйнштейна.
Рис. 6.5. А. Эйнштейн
К 1905 г. была создана специальная теория относительности . Специальная теория относительности (СТО) представляет собой современную физическую теорию пространства и времени, в которой, как и в классической ньютоновской механике, предполагается, что время однородно, а пространство однородно и изотропно. СТО основана на двух постулатах.
Принцип относительности:
Никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.
Принцип инвариантности скорости света:
Скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.
Первый постулат является обобщением механического принципа относительности Галилея на все явления природы. Согласно второму постулату, постоянство скорости света — фундаментальное свойство природы, которое констатируется как опытный факт. Выше мы использовали этот постулат в форме уравнений движения светового импульса
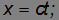
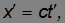
Из этих постулатов следует необходимость замены преобразований Галилея преобразованиями Лоренца.
Непосредственное следствие преобразований Лоренца: не может быть объектов, движущихся быстрее света. С такими объектами можно было бы связать систему отсчета, а при V > c для координат и времен получатся мнимые значения. Выходит, что скорость света играет роль предельно возможной скорости распространения сигнала.
Инвариантность интервала. Пусть даны два события: одно произошло в момент времени t1 в точке с координатами x1, y1, z1, а второе — в момент времени t2 в точке с координатами x2, y2, z2.
Интервалом между событиями называется величина
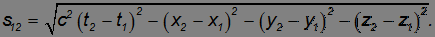
Поставив над координатами и временами штрихи, мы получим величину интервала s'12 между этими же событиями в другой системе отсчета. Из преобразований Лоренца находим:

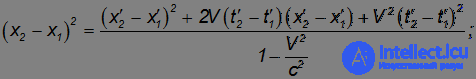
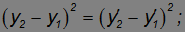
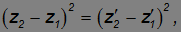
откуда следует:
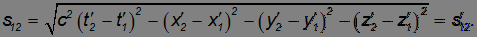
Таким образом,
Величина интервала является инвариантом относительно преобразований Лоренца.
В классической механике таким свойством обладали по отдельности временной интервал
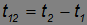
и пространственное расстояние
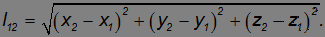
В релятивистской физике (от англ. relativity — относительность) этим свойством обладает только интервал между событиями
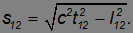
Замедление времени. Пусть в начале координат системы К' закреплены часы: их координаты равны тогда х' = у' = z' = 0, a t' — показываемое ими время (то есть время в системе отсчета К'). Подставляя эти значения в уравнения преобразований Лоренца, находим обычные выражения для координат этих часов в системе К: х = Vt, у = z = 0 (то есть в системе К часы движутся со скоростью V вдоль оси х). Удивительным является последнее уравнение — преобразование времени:
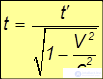
или
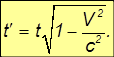
Время t', отсчитываемое часами в системе К', меньше времени t, отсчитываемого часами системы К.
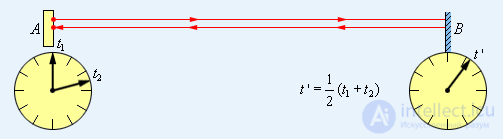
Рис. 6.6. Согласование показаний часов у наблюдателей А и В
Время t', показываемое часами в системе отсчета, где они покоятся, называется собственным временем.
Конкретное устройство часов здесь не играет никакой роли: речь идет о том, что временной интервал не является больше инвариантом и различен для разных систем отсчета. Об этом говорит сайт https://intellect.icu . Это демонстрирует следующий пример.
Пример 1. Время жизни τ0 покоящегося мюона (одной из элементарных частиц) равно 2,2 мкс. От точки рождения до детектора, зарегистрировавшего его распад, мюон пролетел расстояние l = 6 км. Определим, с какой скоростью v (в долях скорости света) летел мюон.
В системе отсчета К', связанной с мюоном, его время жизни равно τ0. В лабораторной системе К, согласно полученному соотношению, от рождения мюона до распада пройдет время
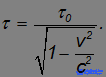
За это время мюон преодолеет расстояние

откуда находим
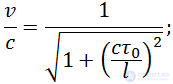
Величина
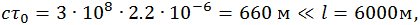
подставляя cτ0 и l в (6.4.1), получаем

Если бы время жизни мюона относительно лабораторной системы К было таким же как и в той системе отсчета, где он покоится, то в лабораторной системе отсчета он пролетел бы расстояние L
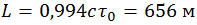
которое более чем в девять раз меньше действительного. Даже если бы он летел не со своей действительной скоростью (6.4.2), а с предельной скоростью c, что невозможно для частицы с отличной от нуля массой, он пролетел бы всего ct0 = 660 м, но никак не 6 км.
Многочисленные наблюдения за элементарными частицами, покрывающими гораздо большие расстояния, чем им позволяет классическая механика, — прямое доказательство реальности эффекта замедления времени.
Рис. 6.7. Распад пи-мезона на мюон и нейтрино
Сокращение длины. Пусть в движущейся системе отсчета вдоль оси 0x закреплена линейка, длина которой (собственная длина) равна l0. Если один конец линейки находится в начале координат (x'1 = 0), а ее другой конец находится в точке с координатой x'2=l0, то из преобразований Лоренца непосредственно следуют координаты концов линейки в системе отсчета К :
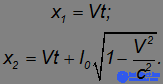
Разность этих координат дает длину линейки в системе отсчета К :

Движущаяся линейка становится короче линейки покоящейся. Этот факт также находится в согласии с утверждением, что в релятивистской механике инвариантом является интервал s12, а не пространственные расстояния. Полученное сокращение длины движущегося объекта напоминает сокращение Фитцджеральда-Лоренца. Но с той разницей, что никакой эфир на объект не действует и никаких механических напряжений в линейке не возникает. Просто длина в движущейся и неподвижной системе отсчета различается, как различаются временные интервалы между двумя событиями. Эти оба эффекта — сокращение длины и замедление времени — связаны друг с другом.
Пример 2. Рассмотрим события, описанные в предыдущем примере, с точки зрения наблюдателя, «сидящего» на мюоне.
В момент рождения мюона детектор, регистрирующий его распад, находился с точки зрения наблюдателя в лаборатории на расстоянии l. С точки зрения наблюдателя на мюоне детектор приближается к мюону со скоростью v, причем начальное расстояние L до него будет меньше:
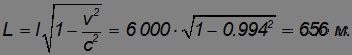
Детектор приблизится к мюону за время
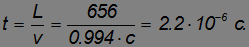
Это время совпадает со временем жизни мюона, который распадется в детекторе, как это видел и неподвижный наблюдатель. Описания событий разные, но оба наблюдателя зафиксируют один и тот же физический факт — распад мюона в детекторе.
Одновременность событий. Пусть имеются два события 1 и 2. Место и время совершения первого из них выберем за начало отсчета соответствующих координат: x1 = 0, t1 = 0. Пусть событие 2 происходит одновременно или позже первого
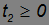
в точке на оси 0x, удаленной на расстояние L. Посмотрим, каковы координаты и моменты времени совершения этих событий с точки зрения наблюдателя, движущегося в положительном направлении оси 0x со скоростью V. Из преобразований Лоренца следует, что x'1 = 0, t'1 = 0, то есть координаты и время совершения первого события не изменяются. Второе же событие произойдет в точке x'2 в момент времени t'2, где
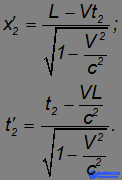
Знак координаты x'2 будет таким же, как и в классической механике. Если наблюдатель не успеет долететь до места совершения события к моменту, когда оно произойдет (Vt2 < L), то событие случится у него впереди по курсу (x'2 > 0), если же успеет (Vt2 > L), — то событие 2 произойдет сзади него (x'2 < 0). Но вот то, что происходит с моментом совершения события 2, не имеет аналога в классической физике. В самом деле, относительно неподвижного наблюдателя событие 2 произошло позже события 1. Но при достаточно большой скорости
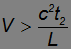
знак у t'2 становится отрицательным, то есть порядок событий меняется!
Но всегда ли это возможно? Ведь события 1 и 2 могут быть причинно связаны друг с другом. Например, событие 1 — рождения отца, а событие 2 — рождение его ребенка. Разве не было бы абсурдным, если бы нашелся наблюдатель, для которого ребенок родился бы прежде отца (нарушилась бы, как говорят, причинно-следственная связь)? Конечно, это невозможно. Давайте сформулируем условие, при котором события 1 и 2 могут быть связаны друг с другом. Так как максимально возможная скорость распространения любого сигнала не превышает c, то события могут находиться в причинно-следственной связи, если они не слишком удалены друг от друга:
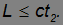
Только тогда «сообщение» о первом событии достигнет второго до его совершения. Но если

то для изменения порядка событий наблюдатель должен двигаться со скоростью
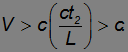
А это, как мы видели, невозможно.
Таким образом, события, которые могут в принципе зависеть друг от друга, имеют тот же временной порядок для всех наблюдателей.
Если же события происходят настолько далеко друг от друга, что они не могут быть связаны никаким сигналом

то порядок совершения этих событий зависит от скорости движения наблюдателя и при
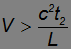
порядок событий будет иным, нежели в неподвижной системе отсчета. В частности, одновременные события (t1 = t2), происходящие в неподвижной системе отсчета на любом расстоянии друг от друга, не могут быть причинно-связанными (для этого нужны были бы сигналы с бесконечно большой скоростью). Из формулы для преобразования времени получаем при t2 = 0:
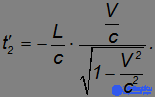
Значит, при любой скорости наблюдателя, движущегося в положительном направлении оси 0x, событие 2 происходит раньше события 1. При движении в обратном направлении (V < 0) событие 2 происходит позже.
Рис. 6.8. События могут быть одновременными, с точки зрения некоего наблюдателя, если ds2 > 0
Проиллюстрируем сказанное на следующем примере. Пусть движется поезд А’В’, в концы которого ударяют две молнии, оставляющее на рельсах отметки А и В (рис. 6.9).
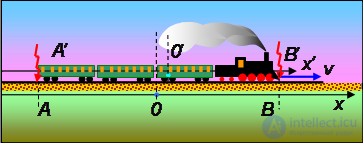
Рис. 6.9. К понятию относительности одновременности
Отметим в поезде среднюю точку 0’, а на полотне — соответственно 0. Свяжем с железнодорожным полотном систему отсчета 0х, а с поездом — систему отсчета 0х’. Пусть в точку 0 вспышки света происходят одновременно. Тогда в неподвижной системе отсчета х оба события (удары молнии) происходят одновременно.
Поскольку поезд движется вправо, и, следовательно, в момент прихода вспышек в середину поезда точка 0’ находится правее 0, то вспышка из точки А’ в точку 0’ придет позже, чем из точки B'. Это означает, что в системе х’ удар молнии в точке В’ происходит раньше, чем в точке А’.
Мы убедились, что наряду с относительностью временных интервалов и пространственных расстояний даже одновременность событий не имеет абсолютного значения. Все они относительны, то есть зависят от движения наблюдателя. В классической физике относительными были, например, скорости тел, их кинетические энергии. Теперь список подобных величин пополнился, только и всего.
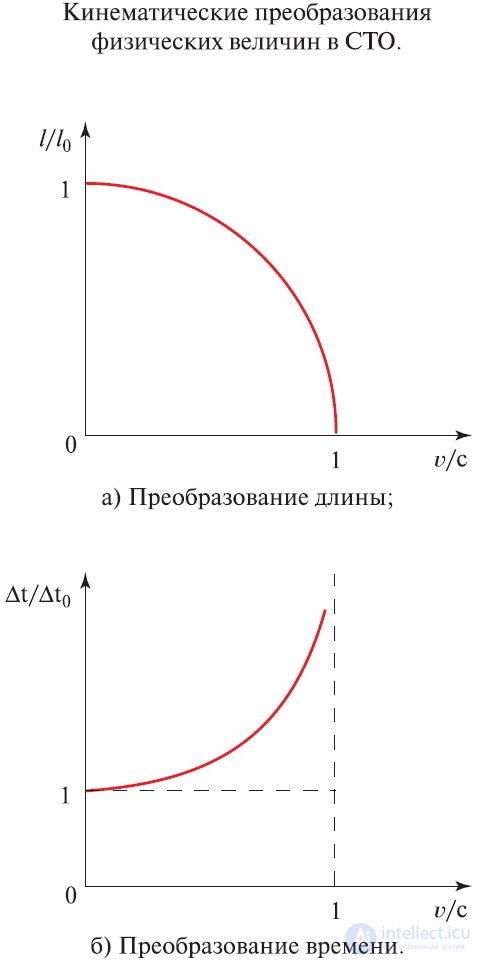
Рис. 6.10. Кинематические преобразования физических величин в СТО
Мы говорили, что скорость света — максимально возможная скорость распространения сигнала. Но что будет, если свет испускается движущимся источником в направлении его скорости V ? Согласно закону сложения скоростей, следующему из преобразований Галилея, скорость света должна быть равна c + V. Но в теории относительности это невозможно. Посмотрим, какой закон сложения скоростей следует из преобразований Лоренца. Для этого запишем их для бесконечно малых величин:
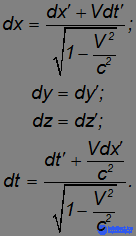
По определению скорости ее компоненты в системе отсчета K находятся как отношения соответствующих перемещений к временным интервалам:
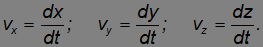
Аналогично определяется скорость объекта в движущейся системе отсчета K', только пространственные расстояния и временные интервалы надо взять относительно этой системы:
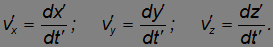
Следовательно, разделив выражение dx на выражение dt, получим:
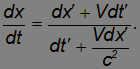
Разделив числитель и знаменатель на dt', находим связь x-компонент скоростей в разных системах отсчета, которая отличается от галилеевского правила сложения скоростей:
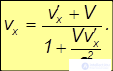
Кроме того, в отличие от классической физики, меняются и компоненты скоростей, ортогональные направлению движения. Аналогичные вычисления для других компонент скоростей дают:
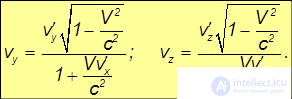
Таким образом, получены формулы для преобразования скоростей в релятивистской механике. Формулы обратного преобразования получаются при замене штрихованных величин на нештрихованные и обратно и заменой V на –V.
Теперь мы можем ответить на вопрос, поставленный в начале данного раздела. Пусть в точке 0' движущейся системы отсчета K' установлен лазер, посылающий импульс света в положительном направлении оси 0'х'. Какой будет скорость импульса для неподвижного наблюдателя в системе отсчета К? В этом случае скорость светового импульса в системе отсчета К' имеет компоненты
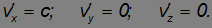
Применяя закон релятивистского сложения скоростей, находим для компонент скорости импульса относительно неподвижной системы К :
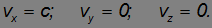
Мы получаем, что скорость светового импульса и в неподвижной системе отсчета, относительно которой источник света движется, равна
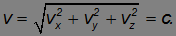
Тот же результат получится при любом направлении распространения импульса. Это естественно, так как независимость скорости света от движения источника и наблюдателя заложена в одном из постулатов теории относительности. Релятивистский закон сложения скоростей — следствие этого постулата.
Действительно, когда скорость движения подвижной системы отсчета V << c, преобразования Лоренца переходят в преобразования Галилея, мы получаем обычный закон сложения скоростей
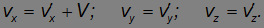
При этом ход течения времени и длина линейки будут одинаковы в обеих системах отсчета. Таким образом, законы классической механики применимы, если скорости объектов много меньше скорости света. Теория относительности не зачеркнула достижения классической физики, она установила рамки их справедливости.
Пример. Тело со скоростью v0 налетает перпендикулярно на стенку, двигающуюся ему навстречу со скоростью v. Пользуясь формулами для релятивистского сложения скоростей, найдем скорость v1 тела после отскока. Удар абсолютно упругий, масса стенки намного больше массы тела.
Воспользуемся формулами, выражающими релятивистский закон сложения скоростей.
Направим ось х вдоль начальной скорости тела v0 и свяжем систему отсчета K' со стенкой. Тогда vx = v0 и V = –v. В системе отсчета, связанной со стенкой, начальная скорость v'0 тела равна
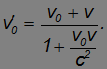
Поскольку стенку можно считать бесконечно массивной, по закону сохранения энергии после упругого удара тело отскочит в обратном направлении с тем же (относительно стенки) абсолютным значением скорости:
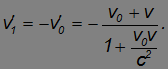
Вернемся теперь назад в лабораторную систему отсчета К. Подставляя в релятивистский закон сложения скоростей v'1 вместо v'x и учитывая опять же V = –v, находим после преобразований:
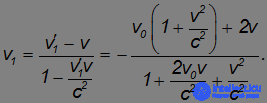
Проанализируем теперь предельные случаи.
Если скорости тела и стенки малы (v0 << с, v << с), то можно пренебречь всеми членами, где эти скорости и их произведение делятся на скорость света. Получаем тогда из найденной формулы результат классической механики
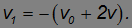
Скорость шара после отскока увеличивается на удвоенную скорость стенки; направлена она, естественно, противоположно начальной. Ясно, что в релятивистском случае этот результат не годится. В частности, при v0 = v = с/3 из него следует, что скорость тела после отскока будет равна v1 = –с, чего не может быть.
Пусть теперь на стенку налетает тело, двигающееся со скоростью света (например, лазерный луч отражается от двигающегося зеркала). Подставляя v0 = с в найденное соотношение, получаем
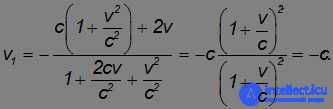
Иными словами, скорость лазерного луча изменила направление, но не свою абсолютную величину, как и должно быть.
Рассмотрим теперь случай, когда стенка движется с релятивистской скоростью. В этом случае найденное соотношение дает нам
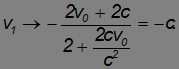
Тело после отскока также будет двигаться со скоростью, близкой к скорости света.
Наконец, подставим в найденное соотношение значения v0 = v = с/3 :

В отличие от классической механики, теория относительности дает для скорости после отскока значение, меньшее скорости света.
Напоследок посмотрим, что случится, если стенка удаляется от тела с той же скоростью (v = –v0). Имеем в этом случае:
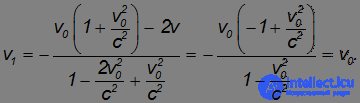
Как и в классической механике, тело стенку не догонит, и его скорость не изменится.
Явление аберрации было открыто Дж. Бредли в 1725 г.: наблюдения показали, что в течение года звезды описывают на небе небольшие эллипсы. Период обращения звезд подсказал, что это явление связано с годовым движением Земли вокруг Солнца. Теоретическое объяснение основывалось на идее сложения скорости луча света от звезды с орбитальной скоростью Земли. Рассказывают, что толчком к пониманию эффекта послужила прогулка Бредли на яхте. Он заметил, что вымпел на мачте вовсе не указывает направления ветра, но меняет свое направление каждый раз при повороте яхты.
Пусть, к примеру, в гелиоцентрической системе отсчета свет от неподвижной в этой системе отсчета звезды М приходит на Землю под углом ψ к направлению движения Земли в момент приема этого света земными детекторами (левая часть рис. 6.11). Ось ОХ выбранной системы отсчета направлена по вектору скорости Земли (красная стрелка на правой части рисунка).
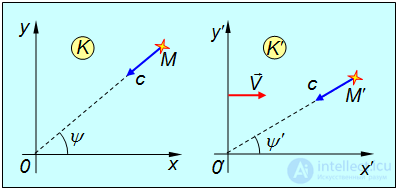
Рис.6.11. Углы наблюдения звезды в различных системах отсчета
В системе отсчета K', связанной с Землей, угол наклона ψ' светового луча будет иным. Действительно, x-компоненты скорости луча света в системах K и K' равны соответственно
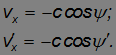
Здесь мы приняли во внимание, что модуль скорости света в обеих системах равен c. С другой стороны, компоненту скорости света в системе K' можно получить из релятивистского закона сложения скоростей
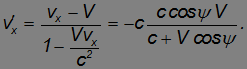
Приравнивая правые части выражений для v'x находим
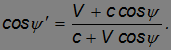
В течение года Земля в неподвижной системе отсчета описывает замкнутую траекторию, ее скорость меняется по величине и направлению, так что периодически меняется и угол наблюдения звезды ψ', в то время как угол ψ остается неизменным. Это и есть явление аберрации.
Применим теперь полученные формулы к случаю наблюдения звездного неба с гипотетического космического корабля, движущегося с большой скоростью. Представим себе, что звезды в неподвижной системе расположены равномерно на небосводе. С точки зрения астрономов на корабле это уже не так. Действительно, звезда сзади по курсу корабля не сдвинется: из наших формул при ψ = 180°, cos ψ = –1 следует, что cos ψ' = –1, ψ' = 180°. Звезда же, расположенная по углом ψ = 90° (cos ψ = 0) к курсу корабля будет наблюдаться космонавтами в направлении cos ψ' = V/c. При V близких к c этот угол очень мал. В этом узком конусе будут сосредоточены все звезды передней (в неподвижной системе отсчета) полусферы. Наоборот, можно показать, что звезды из узкого конуса с тем же углом раствора, но сзади по курсу, займут всю заднюю полусферу в системе отсчета K'. Таким образом, при увеличении скорости корабля небо позади остается почти пустынным, в то время как почти вся видимая Вселенная сольется в яркое пятно впереди по курсу.
Масса элементарной частицы является ее инвариантной характеристикой и не зависит от того, движется или покоится частица. Однако, введенное ранее выражение для импульса
|
|
(6.7.1) |
приближенно справедливо только при нерелятивистских (v << c) скоростях частицы. Не следует придавать словам «приближенно справедливо» излишнего драматического значения по той простой причине, что когда речь идет о движении макроскопических тел, эти поправки ничтожно малы. Например, орбитальная скорость Земли составляет 30 км/с, чему соответствуют релятивистские поправки, по порядку величины равные (v/c)2 ~ 10–8. Однако, при рассмотрении движения элементарных частиц (электронов, протонов и т.п.) релятивистские поправки чаще всего уже не малы: правильные релятивистские значения физических характеристик могут в тысячи раз превышать свои значения, рассчитанные по нерелятивистским формулам.
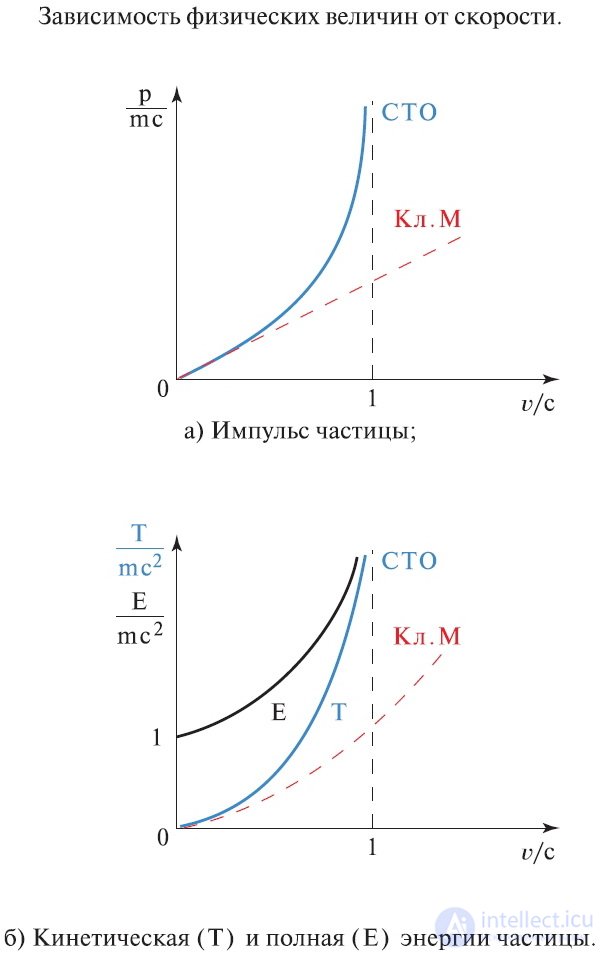
Рис. 6.12. Зависимость физических величин от скорости
Предположим, что справедливое и в релятивистском (v ~ c) случае выражение для импульса свободной частицы массы m, движущейся в нашей системе отсчета со скоростью 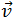 можно записать в виде
можно записать в виде
|
|
(6.7.2) |
где 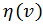 — некоторая функция только модуля скорости. Свободная частица — это замкнутая система из одной частицы, для замкнутой системы пространство изотропно (один из проверенных временем всеобщих постулатов современной физики), поэтому вектор импульса обязан быть направленным по единственному вектору в задаче, а именно: вектору скорости частицы
— некоторая функция только модуля скорости. Свободная частица — это замкнутая система из одной частицы, для замкнутой системы пространство изотропно (один из проверенных временем всеобщих постулатов современной физики), поэтому вектор импульса обязан быть направленным по единственному вектору в задаче, а именно: вектору скорости частицы 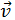 , по этой же причине его модуль не может зависеть от того, в каком направлении движется частица, следовательно
, по этой же причине его модуль не может зависеть от того, в каком направлении движется частица, следовательно  . Выражение (6.7.2) — это импульс, то есть по размерности, это произведение массы на скорость, следовательно функция безразмерна. Соответственно, она не может зависеть просто от модуля скорости частицы v, так как это размерная величина. Возможна лишь зависимость от безразмерного отношения скорости частицы к какой-то другой скорости. Нетрудно сообразить, что это должна быть инвариантная скорость, иначе при одной и той же скорости частицы это отношение, а вместе с ним функция
. Выражение (6.7.2) — это импульс, то есть по размерности, это произведение массы на скорость, следовательно функция безразмерна. Соответственно, она не может зависеть просто от модуля скорости частицы v, так как это размерная величина. Возможна лишь зависимость от безразмерного отношения скорости частицы к какой-то другой скорости. Нетрудно сообразить, что это должна быть инвариантная скорость, иначе при одной и той же скорости частицы это отношение, а вместе с ним функция  и сам импульс будут принимать различные значения, что противоречит здравому смыслу. В нашем распоряжении есть только одна инвариантная скорость: это скорость света в вакууме с. Таким образом, имеем:
и сам импульс будут принимать различные значения, что противоречит здравому смыслу. В нашем распоряжении есть только одна инвариантная скорость: это скорость света в вакууме с. Таким образом, имеем:
|
|
(6.7.3) |
Релятивистское выражение для импульса (6.7.2) должно при малых скоростях переходить в нерелятивистское выражение (6.7.1), поэтому можно утверждать, что
|
|
(6.7.4) |
Установить вид функции  (v) можно разными способами, в частности, следующим образом.
(v) можно разными способами, в частности, следующим образом.
Представим себе, что в неподвижной системе отсчета вдоль оси 0x движется тело массой m и на него в направлении движения в течение короткого времени dt действует сила F. Под действием этой силы тело приобретает скорость v + dv. Изменение импульса тела равно
|
|
(6.7.5) |
Рассмотрим движение этого тела в системе отсчета K', движущуюся вдоль оси 0x со скоростью V равной скорости тела до действия на него силы, то есть V = v. Это так называемая сопутствующая система отсчета, в этой системе отсчета тело первоначально (до начала действия силы) покоилось, а после действия силы приобрело скорость dv'. Поскольку речь идет о бесконечно малой скорости тела, то в этой системе отсчета применимы законы нерелятивистской механики. Следовательно, в К' скорость, приобретенная телом, равна
|
|
(6.7.6) |
Скорости тела в K – v + dt и в K' – dv' связаны релятивистским законом преобразования скоростей, в котором надо положить V = v :
|
|
(6.7.7) |
Бесконечная малость dv' позволяет переписать дробь 1/(1 + vdv'/c2) в следующем виде 1/(1 + vdv'/c2) = 1 – vdv'/c2. Подставляя это соотношение в (6.7.7), получаем
|
|
(6.7.8) |
В самом правом выражении в (6.7.8) опущено слагаемое второго порядка малости пропорциональное (dv')2. Сократив слева и справа скорость v, получаем связь между приращениями скорости в системах отсчета К и К'
|
|
(6.7.9) |
Подстановка в (6.7.9) второго закона Ньютона в виде (6.7.6) дает
|
|
(6.7.10) |
И, наконец, подстановка (6.7.10) в выражение для приращения импульса (6.7.5)
|
|
(6.7.11) |
Время действия силы dt' в системе К' связано с ее временем действия dt в системе К соотношением
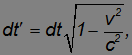
позволяющим приращение импульса в системе К выразить через время действия силы dt в той же системе К. Таким образом, для скорости изменения импульса в системе К имеем:
|
|
(6.7.12) |
Теперь самое главное: следуя принципу относительности, гласящему, что законы природы должны выглядеть одинаково во всех инерциальных системах отсчета, потребуем, чтобы и в системе К (сравним со вторым уравнением в (6.7.6)) второй закон Ньютона имел вид
|
dp/dt=F |
(6.7.13) |
Сравнивая (6.7.12) и (6.7.13) для функции η(ξ) получаем следующее дифференциальное уравнение
|
|
(6.7.14) |
Путем прямого дифференцирования функции
|
|
(6.7.15) |
легко убедиться в том, что она является решением уравнения (6.7.14) и удовлетворяет условию перехода к нерелятивистскому пределу (6.7.4).
Релятивистское выражение для импульса, удовлетворяющее всем сформулированным выше условиям и справедливо при любых скоростях имеет вид:
|
|
(6.7.16) |
Или короче, используя релятивистский фактор 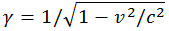
|
|
(6.7.17) |
При малых скоростях выражение v << c переходит в нерелятивистское выражение ньютоновской механики 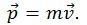
Релятивистский импульс бесконечно растет при приближении скорости тела к скорости света. Зависимость релятивистского импульса частицы от ее скорости представлена на рис. 6.13.
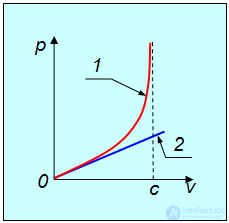
Рис. 6.13. Зависимость импульса частицы от ее скорости: 1 — релятивистский импульс; 2 — ньютоновский импульс
Пример. Тело начинает двигаться из состояния покоя под действием постоянной во времени силы F. Найдем зависимость скорости тела от времени и сравним с классическим результатом.
Так как скорость тела в этом случае будет направлена вдоль линии действия силы, можно записать основное уравнение динамики в скалярной форме:
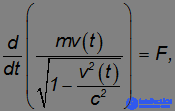
где v(t) — скорость тела в момент времени t, причем v(0)=0. Интегрируя, находим:
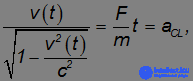
где мы ввели обозначение aCL = F/m для классического ускорения тела. Возводя уравнение в квадрат, легко получаем закон зависимости скорости от времени:
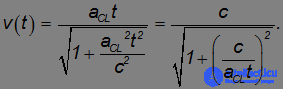
Таким образом, в любой момент времени v(t) < c, а при

В случае небольших значений времени (t << c/aCL) мы получаем результат классической нерелятивистской механики для равноускоренного движения:
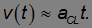
Приведем численные оценки. Пусть ракета движется с ускорением (классическим) aCL=g = 9,8 м/с2 (то есть космонавты испытывают привычную земную силу тяжести). Согласно классическому закону движения ракета достигнет скорости света через время
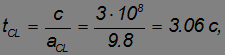
то есть примерно через год. На самом деле в этот момент времени ее скорость будет равняться
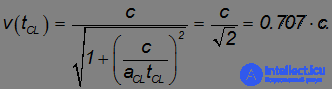
Через два года пути скорость станет равной
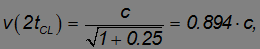
через пять лет будет

через 10 лет получим
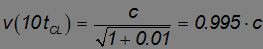
и так далее.
Сколько бы времени ни ускорялась ракета, ее скорость никогда не достигнет скорости света. Скорость ракеты, как принято говорить у математиков, будет асимптотически приближаться к скорости света в вакууме и станет ей равна через бесконечное время.
Итак, релятивистское уравнение движения материальной точки, или основное уравнение релятивистской динамики, имеет обычный вид уравнения второго закона Ньютона, но с другой зависимостью импульса от скорости:

Преобразуем приращение импульса в левой части этого уравнения:
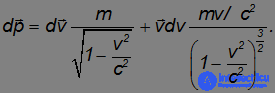
Умножим основное уравнение релятивистской динамики скалярно на вектор перемещения

Справа мы имеем обычное выражение для изменения кинетической энергии тела:

Слева после учета, что
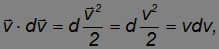
можно получить
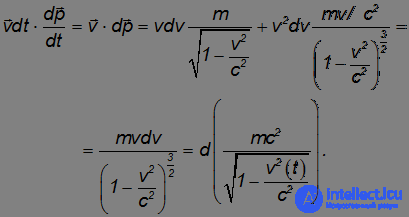
Таким образом,
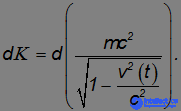
Следовательно, выражение в скобах справа с точностью до постоянной интегрирования представляет собой кинетическую энергию материальной точки, движущейся со скоростью v. Значение этой постоянной фиксируется условием, что К = 0 при v = 0.
Окончательно получаем релятивистское выражение для кинетической энергии
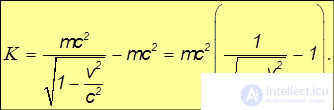
Или короче, используя релятивистский фактор 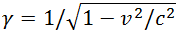 :
:
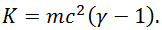
При малых скоростях v << с мы можем разложить квадратный корень в ряд Тейлора по степеням отношения v/c. Оставляя первые два члена ряда, имеем
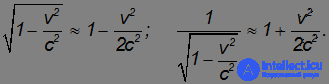
В этом приближении кинетическая энергия определяется классической формулой
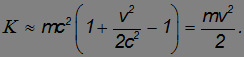
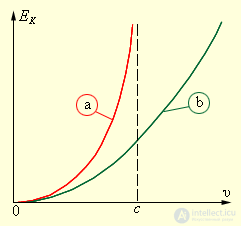
Рис. 6.14. Зависимость кинетической энергии от скорости. а – релятивистское значение, b – классическое значение кинетической энергии.
В теории относительности пространство и время не являются более независимыми: из преобразований Лоренца и инвариантности интервала видно, что они входят в уравнения на равных правах, образуя единое пространство-время. Вспомним, что законы сохранения импульса 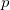 и энергии
и энергии 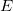 тела связаны с однородностью пространства и времени, соответственно. При переходе к движущейся системе отсчета выражения для импульса и энергии должны преобразовываться аналогично координатам и времени в преобразованиях Лоренца. Выполненные ниже на базе аналогий и анализа размерностей преобразования не являются вполне строгими, но приводят к правильному результату. Строгие выкладки требуют использования аппарата 4х-векторов в четырехмерном пространственно-временном континууме, что выходит за рамки наших нынешних задач. Посмотрим на уравнения, описывающие преобразования Лоренца
тела связаны с однородностью пространства и времени, соответственно. При переходе к движущейся системе отсчета выражения для импульса и энергии должны преобразовываться аналогично координатам и времени в преобразованиях Лоренца. Выполненные ниже на базе аналогий и анализа размерностей преобразования не являются вполне строгими, но приводят к правильному результату. Строгие выкладки требуют использования аппарата 4х-векторов в четырехмерном пространственно-временном континууме, что выходит за рамки наших нынешних задач. Посмотрим на уравнения, описывающие преобразования Лоренца
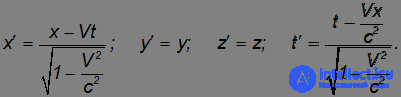
Если заменить в первом из них

то время 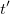 надо заменить на величину, пропорциональную энергии в системе отсчета
надо заменить на величину, пропорциональную энергии в системе отсчета 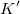 . Коэффициент пропорциональности следует из соображений размерности: энергию надо разделить на квадрат какой-то скорости. У нас есть лишь одна выделенная скорость — скорость света. Аналогично, в последнем уравнении меняем
. Коэффициент пропорциональности следует из соображений размерности: энергию надо разделить на квадрат какой-то скорости. У нас есть лишь одна выделенная скорость — скорость света. Аналогично, в последнем уравнении меняем
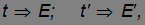
а координату 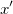 — на величину, пропорциональную импульсу
— на величину, пропорциональную импульсу  . В результате записываем преобразования Лоренца для импульса и энергии в системах отсчета
. В результате записываем преобразования Лоренца для импульса и энергии в системах отсчета 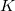 и
и 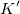 :
:
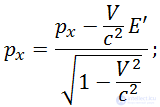
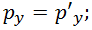
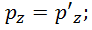
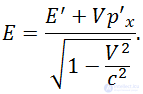
Обратные преобразования имеют вид:
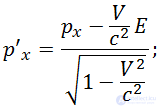
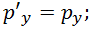
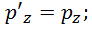
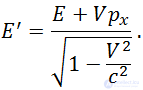
Или, короче, с использованием релятивистского фактора 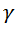
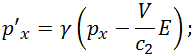
|
|
(6.9.1) |
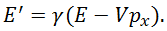
Что такое релятивистский импульс — мы уже знаем. Но что такое релятивистская энергия 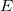 ? Именно эта величина выступает партнером импульсу в преобразованиях Лоренца для импульса и энергии, именно она связана со свойствами пространства-времени и должна сохраняться в замкнутых системах. Применим полученные формулы к точке массой
? Именно эта величина выступает партнером импульсу в преобразованиях Лоренца для импульса и энергии, именно она связана со свойствами пространства-времени и должна сохраняться в замкнутых системах. Применим полученные формулы к точке массой  , движущейся вдоль оси
, движущейся вдоль оси  с постоянной скоростью
с постоянной скоростью  . Ее импульс равен
. Ее импульс равен

Свяжем с точкой систему отсчета 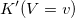 . В этой системе точка покоится, то есть
. В этой системе точка покоится, то есть 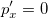 . Подставим эти соотношения в первую из формул (6.9.1)
. Подставим эти соотношения в первую из формул (6.9.1)
|
|
(6.9.2) |
Откуда для энергии частицы массы m, движущейся в нашей системе отсчета со скоростью v, получаем
|
|
(6.9.3) |
В системе отсчета, в которой частица покоится, как следует из (6.9.3), ее энергия равна
|
|
(6.9.4) |
Результат (6.9.4) можно получить и так. В последнюю из формул (6.9.1) подставим импульс p = mvγ и энергию E = mc2γ из (6.9.3), получаем
|
|
(6.9.5) |
Мы получили очень интересные результаты. В системе 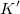 точка покоится, но ее энергия отлична от нуля. Ее так и называют — энергия покоя и обозначают
точка покоится, но ее энергия отлична от нуля. Ее так и называют — энергия покоя и обозначают 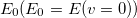
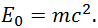
Мы пришли к знаменитой формуле Эйнштейна. Полная энергия движущегося тела дается суммой энергий покоя и кинетической энергии
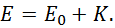
Энергия покоя, сосредоточенная в теле, огромна. Для примера: килограмм угля при сжигании дает около 30 МДж = 3·107 Дж энергии. Энергия же покоя того же килограмма равна 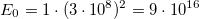 Дж, то есть в три миллиарда раз больше. При некоторых условиях энергия покоя может быть выделена. К сожалению, на практике это впервые было осуществлено при взрыве атомной бомбы.
Дж, то есть в три миллиарда раз больше. При некоторых условиях энергия покоя может быть выделена. К сожалению, на практике это впервые было осуществлено при взрыве атомной бомбы.
Из релятивистских выражений для импульса 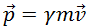 и энергии
и энергии 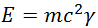 нетрудно получить связь между ними:
нетрудно получить связь между ними:
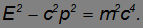
Отсюда следует, что левая часть полученного выражения является инвариантом, то есть не зависит от системы отсчета. Это же можно получить из преобразований Лоренца. Итак, зная импульс тела, можно найти его энергию
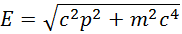
и скорость
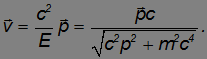
Связь кинетической энергии с импульсом:
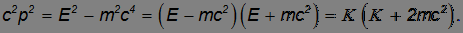
Релятивистские соотношения между энергией тела, его импульсом и скоростью можно изобразить графически в виде прямоугольного треугольника (рис. 6.15), облегчающего запоминание формул.
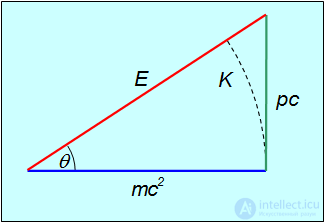
Рис. 6.15. Графическое представление соотношения между энергией и импульсом тела
При бесконечно больших импульсах энергия тела неограниченно растет, а скорость стремится к скорости света. Наоборот, при малых импульсах имеем:
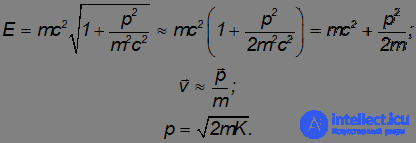
Мы снова пришли к нерелятивистским соотношениям для кинетической энергии и скорости частицы как функций ее импульса.
Из всего сказанного следуют критерии применимости классической механики Ньютона — Галилея:
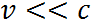
или
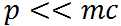
или
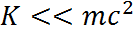
Все выписанные соотношения эквивалентны, из любого из них следуют остальные.
Пример. Солнечная постоянная C (плотность падающего на Землю потока энергии излучения Солнца) равна 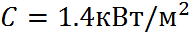 . Определим массу
. Определим массу 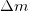 , которую теряет Солнце за один год.
, которую теряет Солнце за один год.
Земля находится от Солнца на расстоянии 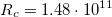 м. За время
м. За время 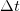 на единицу площади попадает энергия
на единицу площади попадает энергия 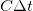 . Умножая на площадь сферы радиусом
. Умножая на площадь сферы радиусом 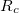 , получаем полную энергию, излученную Солнцем за время
, получаем полную энергию, излученную Солнцем за время 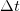 :
:
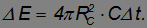
Эта энергия возникает в результате термоядерных реакций за счет уменьшения энергии покоя Солнца. Следовательно, его масса за год уменьшится на величину
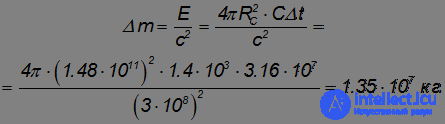
За время своего существования (5 млрд лет) Солнце потеряло в массе 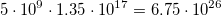 кг. Учитывая, что масса Солнца равна
кг. Учитывая, что масса Солнца равна 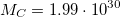 кг, потери массы на излучение составляют 0,03 %. Пример демонстрирует важный вывод теории относительности:
кг, потери массы на излучение составляют 0,03 %. Пример демонстрирует важный вывод теории относительности:
В природе нет закона сохранения массы, есть лишь закон сохранения полной энергии.
Закон сохранения массы возник в классической физике только потому, что кинетические энергии продуктов химических реакций в сотни миллионов раз меньше их энергий покоя. Так что, в химических реакциях масса сохраняется с точностью порядка миллионных долей процента.
Рассмотрим релятивистское выражение, связывающее энергию и импульс:
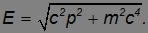
Положив в этом соотношении 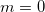 , получим
, получим
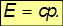
С другой стороны, модуль импульса частицы связан с ее скоростью соотношением
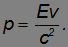
Подставляя сюда полученное выражение для энергии частицы с нулевой массой, получаем  . Частицы нулевой массы не могут покоиться и не могут двигаться иначе как со скоростью света! К числу таких частиц принадлежит световая частица, называемая фотоном (обозначается символом
. Частицы нулевой массы не могут покоиться и не могут двигаться иначе как со скоростью света! К числу таких частиц принадлежит световая частица, называемая фотоном (обозначается символом 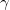 ), a также нейтрино (обозначается
), a также нейтрино (обозначается  ). У таких частиц нет энергии покоя
). У таких частиц нет энергии покоя 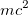 , так как они никогда не покоятся. Но энергией они обладают, что каждый может ощутить на практике, загорая на пляже. На рис. 10 это соответствует предельному случаю, когда нижний катет равен нулю, а гипотенуза совпадает с другим катетом и кинетической энергией:
, так как они никогда не покоятся. Но энергией они обладают, что каждый может ощутить на практике, загорая на пляже. На рис. 10 это соответствует предельному случаю, когда нижний катет равен нулю, а гипотенуза совпадает с другим катетом и кинетической энергией: 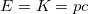 .
.
Пример. Элементарная частица, называемая нейтральным пи-мезоном (обозначение 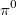 ) распадается на два фотона:
) распадается на два фотона:
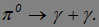
Определим импульсы фотонов, если распавшийся пи-мезон покоился. Масса частицы 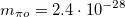 кг.
кг.
Так как вначале пи-мезон покоился, полный импульс системы был равен нулю. Вследствие закона сохранения импульсы фотонов 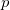 равны по величине и направлены в противоположные стороны. Следовательно, равны и энергии фотонов
равны по величине и направлены в противоположные стороны. Следовательно, равны и энергии фотонов 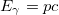 . Записываем закон сохранения энергии в этой реакции:
. Записываем закон сохранения энергии в этой реакции:
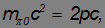
откуда импульсы фотонов равны
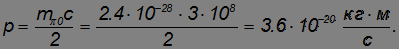
При этом энергия каждого фотона равна половине энергии покоя пи-мезона.
В дальнейшем мы узнаем, что энергия фотона связана с частотой световой волны  соотношением
соотношением
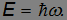
Фотон обладает также импульсом
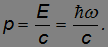
Падая на поверхность, фотоны передают ей свой импульс и оказывают тем самым давление. Обнаружить и измерить световое давление удалось П.Н. Лебедеву в 1900 г.
В 1916 г. А. Эйнштейн, обобщая идеи специальной теории относительности (СТО) на неинерциальные системы, создал теорию гравитации, которую называют также общей теорией относительности — ОТО. Согласно этой теории, любой объект, обладающий энергией 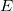 , будет подвержен действию гравитационного поля как если бы он имел гравитационную массу
, будет подвержен действию гравитационного поля как если бы он имел гравитационную массу 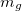 . Связь
. Связь 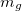 с энергией тела дается уже знакомым соотношением
с энергией тела дается уже знакомым соотношением
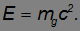
Масса фотона равна нулю, но в любом гравитационном поле он должен вести себя как частица с гравитационной массой
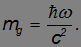
При движении фотона вблизи поверхности Земли вверх по вертикали фотон должен затратить часть своей энергии на совершение работы против сил тяжести:
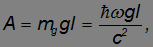
где 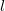 — пройденный по вертикали путь. Соответственно первоначальная энергия фотона, равная
— пройденный по вертикали путь. Соответственно первоначальная энергия фотона, равная
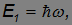
должна уменьшиться на величину 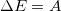 . Значит, частота фотона в конце пути будет меньше на величину
. Значит, частота фотона в конце пути будет меньше на величину 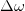 :
:
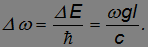
Относительное уменьшение частоты фотона
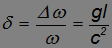
при распространении по вертикали было измерено в 1960 г. американскими учеными Паундом и Ребкой. В условиях опыта оно составило малую величину, равную 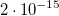 . Значит, перепад высот в опыте Паунда — Ребки составлял
. Значит, перепад высот в опыте Паунда — Ребки составлял
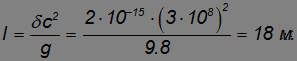
Эффект изменения частоты света при удалении от большой тяготеющей массы называется гравитационным красным смещением.
Исследование, описанное в статье про специальная теория относительности, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое специальная теория относительности, преобразования галилея, преобразования лоренца, постулаты эйнштейна, сложение скоростей в релятивистской механике, аберрация света, частицы с нулевой массой и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Физические основы механики
Комментарии
Оставить комментарий
Физические основы механики
Термины: Физические основы механики